熵
熵的计算公式为:
H(x)=−∑p(x)logp(x)
这个公式我们并不陌生,在决策树切割的时候会记住熵增益,逻辑回归的损失函数交叉熵函数等,那我们今天就来认识一下这个这个熵有何种物理意义。
若不确定性越大,则信息量越大,熵越大
若不确定性越小,则信息量越小,熵越小
当p(x)=0.5的时候,熵最大,不确定性最大。
条件熵
假设随机变量(X,Y),其联合概率分布为
P(x=xi,y=yj)=pij
条件熵H(Y∣X)表示在已知随机变量X的条件下随机变量Y的不确定性。
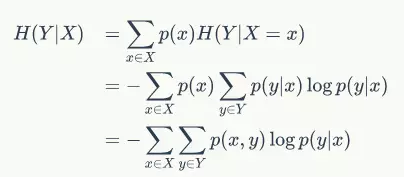
上面这个推导相对比较清晰,从熵的公式定义出发。
注意,这个条件熵,不是指在给定某个数(某个变量为某个值)的情况下,另一个变量的熵是多少,变量的不确定性是多少?而是期望!
因为条件熵中X也是一个变量,意思是在一个变量X的条件下(变量X的每个值都会取),另一个变量Y熵对X的期望。
举个栗子
盗取一份数据,我们就不用为精心构造一个例子为发愁。
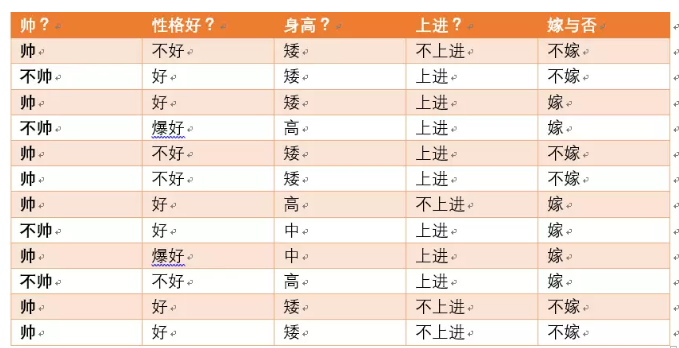
设随机变量Y=
嫁和不嫁的个数分别占一半,根据熵的公式我们很容易计算H(Y),为了计算条件熵,我们引入另一个变量,帅或是不帅。
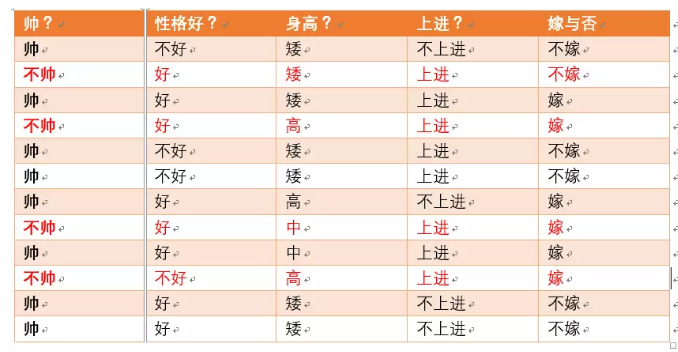
满足条件的只有4个数据了,这四个数据中,不嫁的个数为1个,占1/4
不帅=0
帅 = 1
H(Y∣X=0)=4−1log41−43log43
‘p(X = 0)=4/12=1/3‘
当已知帅的条件下,满足条件的有8个数据了,这八个数据中,不嫁的个数为5个,占5/8
嫁的个数为3个,占3/8
那么此时的
H(Y∣X=1)=8−5log85−83log83
‘p(X=1)=8/12=2/3‘
现在我们要求一个条件熵
H(Y∣X)
其中X当然就是长相了(帅|不帅)
条件熵是另一个变量Y熵对X(条件)的期望
公式为:
H(X)=∑p(x)H(Y∣X=x)
H(Y|X=长相)= p(X=帅)H(Y|X=帅)+p(X=不帅)H(Y|X=不帅)
联合熵
联合熵的定义十分简单
‘H(X,Y)=-\sum p(x,y) log p(x,y)‘
联合熵描述的是一对随机变量X和Y的不确定性。p(x,y)表示两个事件公共发生的概率。
相对熵
相对熵,又称互熵,交叉熵,K-L散度等。用来衡量两个概率分布之间的差异。
设有两个概率分布p(x)和q(x),则p对q的相对熵为:
D(p∣∣q)=−∑p(x)logqp
1.相对熵可以度量两个随机变量的“距离”。
2.在概率和统计学中,经常会使用一种近似的分布来代替复杂的分布。K-L散度度量了使用一个分布来近似另一个分布时所损失的信息。
自信息
自信息表示事件X发生的不确定性,也用来表示时间所包含的信息量
I(X)=−log2P(X)
互信息
事件X Y之间的互信息等于X的自信息减去Y条件下的自信息。
I(X;Y)=H(X)−H(X∣Y)=log2P(X)P(Y)P(X,Y)
互信息是一直Y值后X不确定性的减少量
总而言之
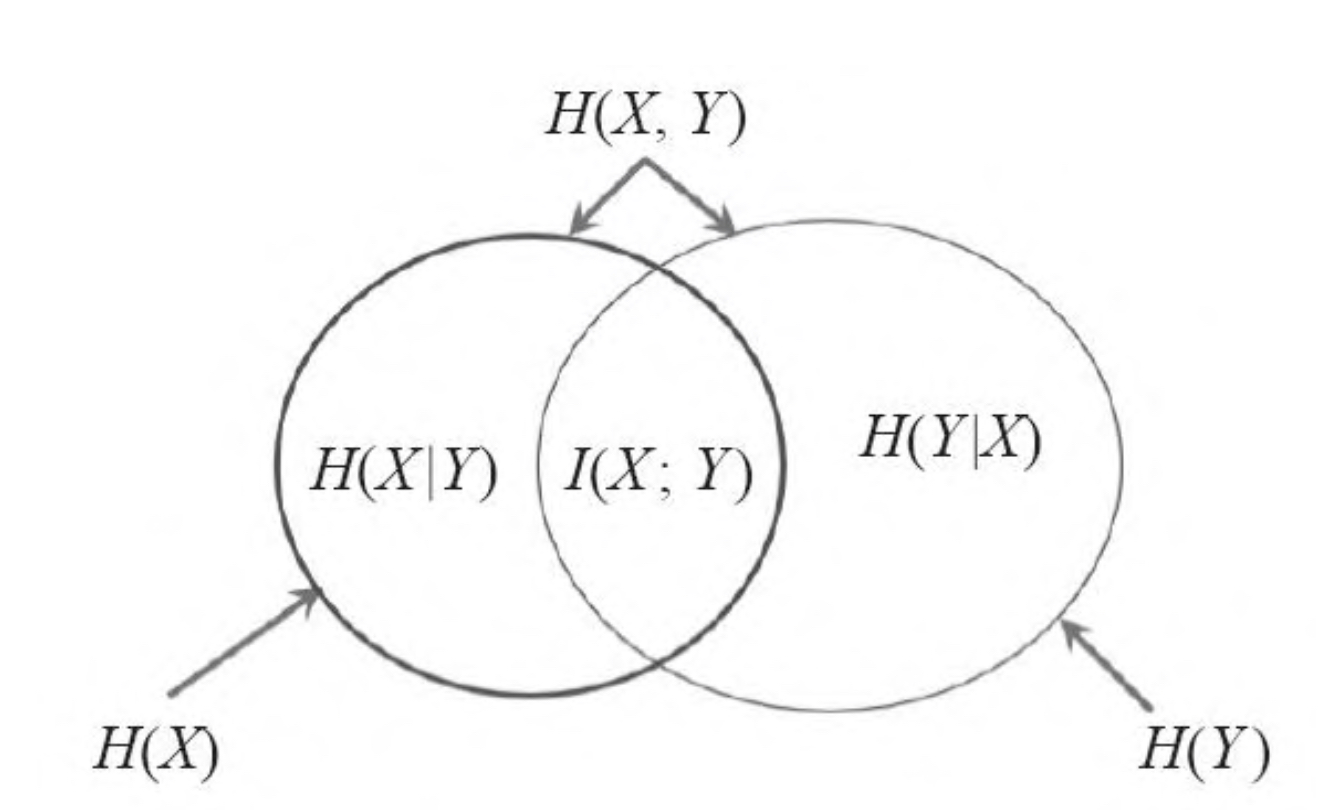
以上就是各种熵之间的关系,总结上每个熵的具体含义,相信你你已经理解了不一样的”熵“