背景介绍
本文算法会解决一个在交通领域的问题,在路网中每天都有一些路段会临时施工和封路,如何无监督的利用现有特征快速发现这些路段是一个比较重要的问题,本文带着这个问题将会介绍一个基于路网异常数据的算法讲解,希望能对大家有些帮助。
首先我们来介绍下这个背景,在交通领域中有一个比较棘手的问题就是如何快速发现异常路段,例如施工、封路,临时交通管制等等。一般的方法实际上是大家会用到一些异常检测算法,或者是一些监督学习的方式,而实际上我们很难获取相应的数据集合,本文提出一个非监督算法来解决这个问题。
定义
偏航:在交通领域中,用户背离导航规划就称为一次偏航。
link: 在交通领域中,我们现实生活中的路段,往往用多条link来表示,而link也是交通领域挖掘的基本单元,本文的异常路段实际上也是异常link定位的算法。
算法讲解
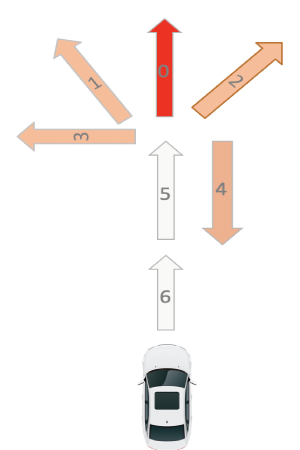
我们来看上面这个图片,其中红色的link0是路网封闭link,用户到达link5以后必须偏航,橘色的link1、link2、link3、link4是可选的偏航link。以下是用户的状态分析:
当用户遇到link0封路的情况下,用户有如下选择,根据目的地选择link1、link2或者link3绕路走,或者原路返回选择link4,就目前用户所处的状态,用户期望转移link0,所以选择link1和link2的概率会大一些,选择link4的可能最小。
如果link0 发生异常,link0上的流量变化会按照一定比例转移到link1,2,3,4上,但是比例会根根与期望夹角的度数概率不断降低。
link0的异常不仅仅需要看link0,link1,2,3,4同样能够验证link0的一样。
用户期望路径5-0, 可选拓扑转角[∠5-1, ∠5-2, ∠5-3, ∠5-4],其中期望转角[∠5-0] 180°,
可选转角[150 °, 200°,90 °,1°], 期望偏差角[∠1-0, ∠2-0, ∠3-0, ∠4-0],且转角度数为[30 °,20 °,90 °,179°],归一化权重[0.375, 0.4, 0.2215,0.0025]。会有如下的一个根据夹角的对应关系。本文称为拓扑卷积核

这个时候我们来看看偏航路段的流量数据。

其中5-0表示link5_0的转移流量变化,从右到左是偏航时间回溯到指定时间间隔的流量序列,将拓扑的流量矩阵构建出来就如上图。
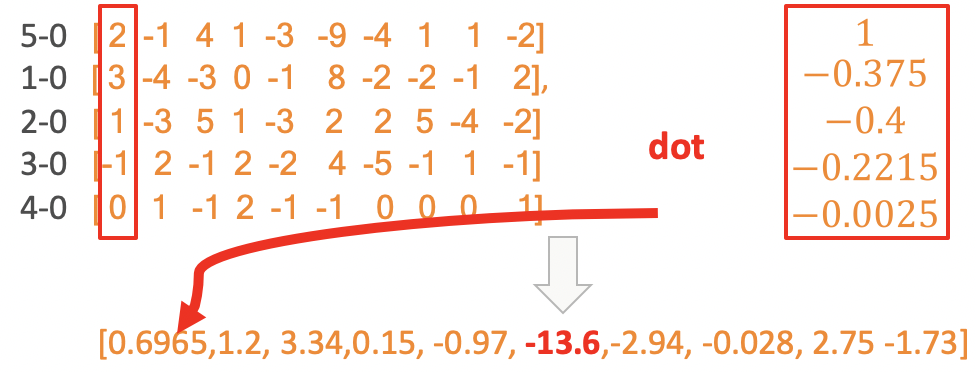
如上图构建出流量差分矩阵,也就是对序列数据按照时间方向进行一次一次差分,然后点乘上文提到的拓扑卷积核。
构建出的序列称为拓扑异常序列
拓扑异常序列:
$$abnormal=[0.6965, 1.2, 3.34, 0.15, -0.97, -13.6,-2.94, -0.028, 2.75 -1.73]$$
$$m = arg min(abnormal) = 6$$
然后拿到我们的link0的流量序列:
$$tested=[10,12,11,15,16,13,4,0,1,2,0]$$
$$normal = mean(10, 12, 11, 15, 16, 13) = 12.83$$
我们根据$m$就能够知道$tested$中那一段是正常序列,哪一段是异常序列,从而计算正常序列均值$normal$.
从而构建target序列:
$$target = [12.83, 12.83, 12.83, 12.83, 12.83, 12.83, 0, 0, 0, 0 ]$$
target序列实际上是我们对于异常pattern的一种描述,也就是期望序列。
$$similarity=cos(test, target ) = 0.9766416071562938$$
$similarity$实际上就是我们对于异常link的一个置信度的描述,这里使用余弦相似度是想要计算两个序列质检趋势的描述。
卷积抽象
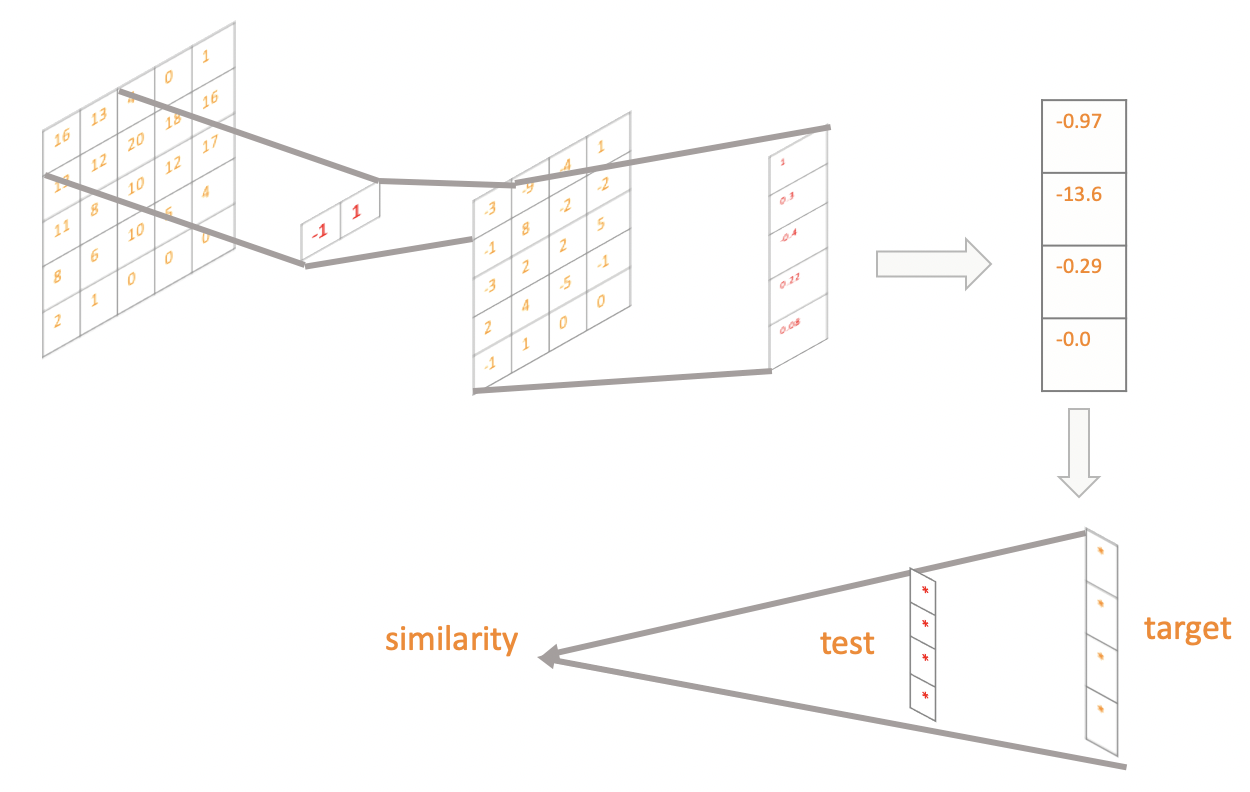
从上文其实我们是能将整个过程做一个卷积抽象,第一层的差分矩阵实际上是对序列进行[-1,1]的一个卷积操作,然后使用拓扑卷积核进行卷积,然后构建target序列,因为是无标注算法,所以置信度就由相似度进行衡量,从这里我们也能了解卷积含义已经过程。