背景
地图匹配算法,在地图领域还是十分重要的算法,那么我们先来普及一下地图匹配算法究竟是做一个什么样的事情呢?
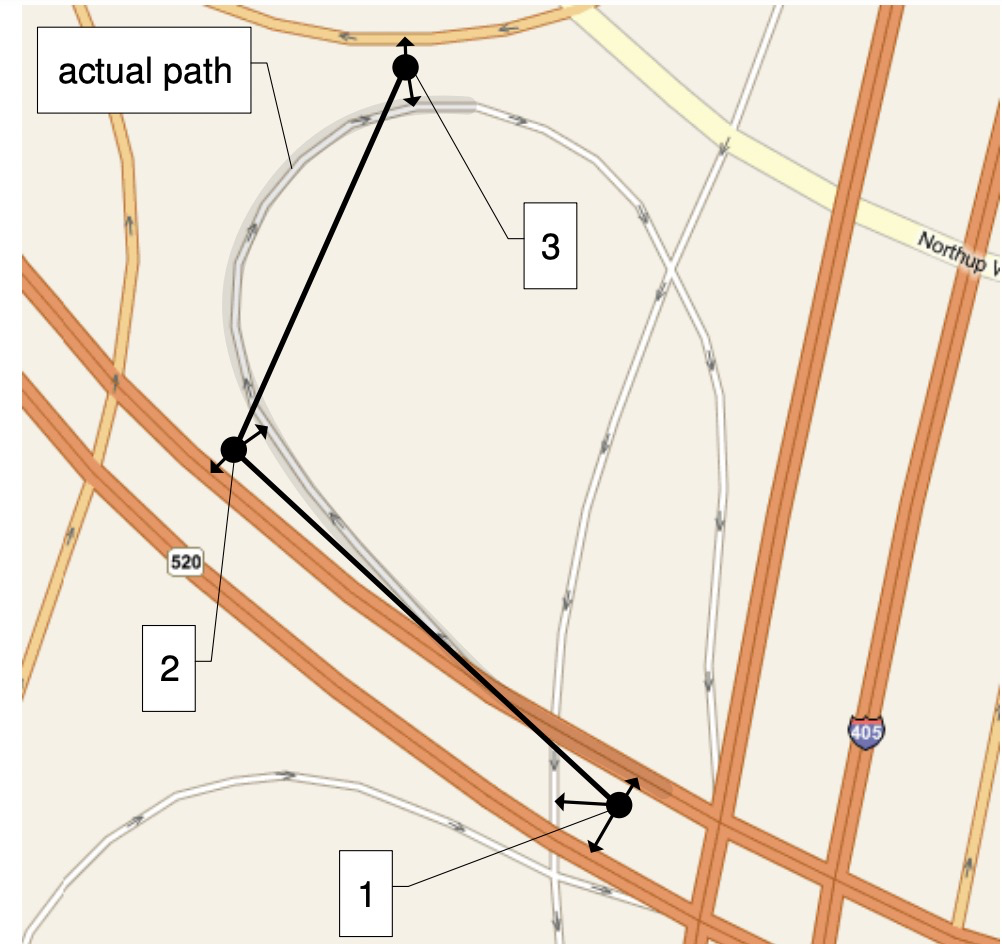
看上面这个图,我们看到三个黑的gps点,和地图一些路网,那么map match解决的就是这三个点究竟在哪条路上?
至于为什么我们要知道这三个点在哪条路上呢? 我们可以这样理解一种业务场景,在轨迹挖掘挖掘中,我们时常希望根据轨迹的数据挖掘出路网的某些路段存在封闭或者开通等情况,但是如果挖掘这样的信息,我们就必须要知道用户是怎么走的,也就是用户的实走轨迹,然后我们地图匹配的算法就是要找到用户的实走轨迹在真实路网的表达。你可能觉得这个不是十分简单吗? 我直接匹配到最近的路上不就可以了吗?在实际的应用场景上,其实是存在以下几个问题的。
- 城市路网复杂,路与路之间十分相近,你很难根据这样一个策略获得匹配的最佳结果。
- gps点本身存在误差,如果与复杂的路网结合,不太可能通过距离找到最优的匹配结果
所以我们来分享一下今天这篇文章,利用HMM思想来做地图匹配的算法。
HMM
基于HMM的算法的套路是我们需要从现有的业务中抽象出一个观察概率,和一个转移概率,那么我来看看在地图匹配中如何定义这两种概率的。
观察概率
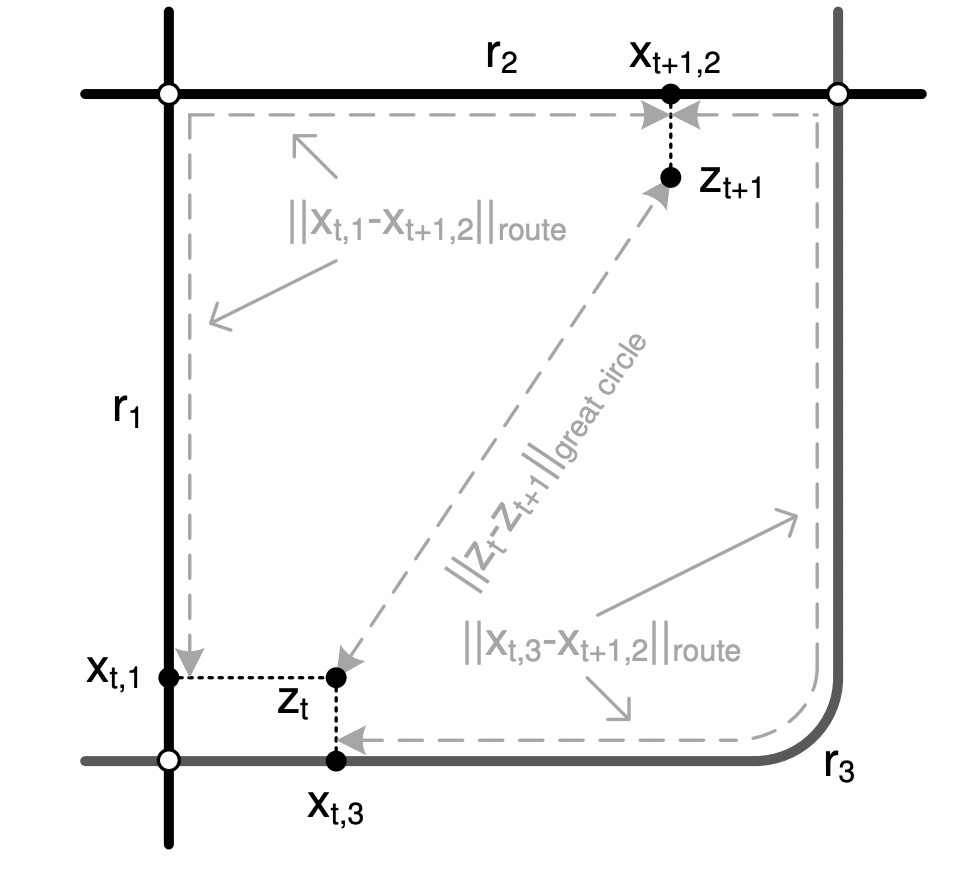
我们先来看上面这个图,我们可以把gps产生的误差分布当成一个标准的高斯分布,也就是均值是0,方差是1的分布,至于这个为什么,大家可以看看这篇文章《VanDiggelen, F., GNSS Accuracy: Lies, Damn Lies, and Statistics, in GPS World. 2007. p. 26-32.》它大致的方法就是获取实际位置和gps位置,然后抽样画图,看看与那种分布拟合程度最好。
所以借此我们能够定义出观察概率的形式
p(zt∣rt)=2πσz1e−0.5(σzzt−xt,i)2(1)
上面的公式参照图上的距离我们来解释一下, ri表示周边实际的道路, ∣∣zt−xt,i∣∣表示候选点zt与到r上的最近的球面距离。σz是gps点的观察点的标准差。
我们可以理解行,点离道路的距离越近,我们就任务属于这条路的概率也就越大,也是比较容易理解的。
转移概率
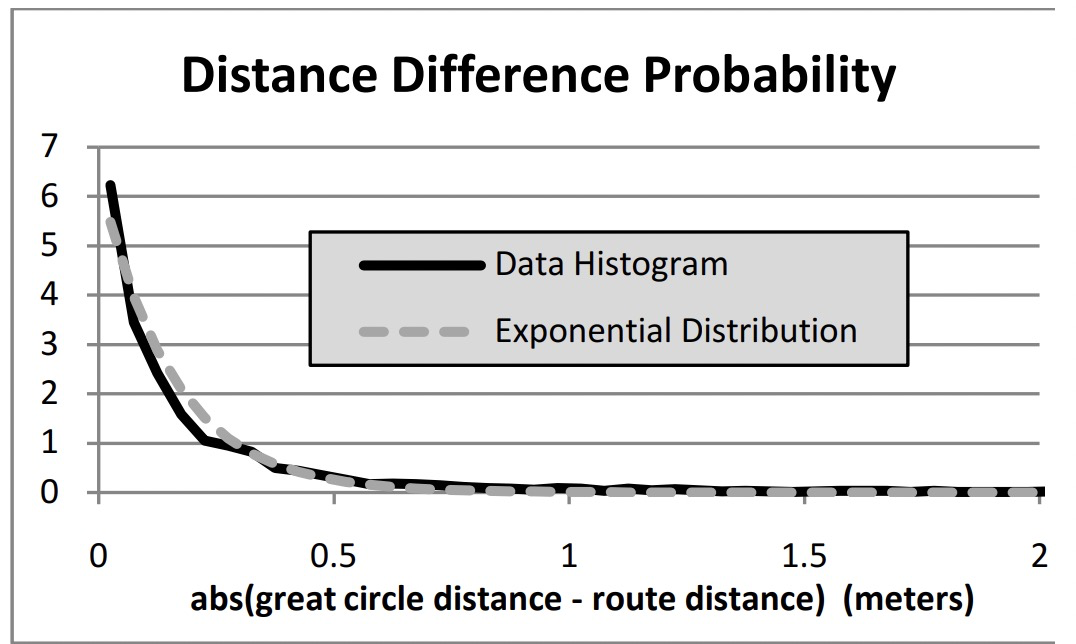
在计算转移概率的时候,作者发现最短路径和观察点之间的球面距离分布式是类似的,分布就如上图所看的。
从而定义出了转移概率的计算
p(dt)=β1eβ−dt(2)
dt=∣∣zt−zt+1∣∣−∣∣xt,i−xt+1,j∣∣(3)
∣∣zt−zt+1∣∣表示观察到之间的球面距离,∣∣xt,i−xt+1,j∣∣是映射点之间的规划最短路径
作者通过实验给出如下的超参的定义σz,β.
σz=1.4826median(∣∣zt−xt,i∣∣)(4)
σz 当你的点质量较差的时候,σz可以设置的大一些。反之亦然
β=ln(2)1median(∣∣zt−zt+1∣∣−∣∣xti−xt+1,j∣∣)(5)
其中∣∣zt−zt+1∣∣是球面距离,∣∣xti−xt+1,j∣∣是规划距离。
β是当然你的r距离和球面距离经常相差较大的时候,这个变量可以设置大一些,一般是点间距比较大导致的
计算
定义好上面的转移概率和观察概率,剩下就是使用维特比(Viterbi)算法计算最优的匹配结果然后输出就可以啦。本文的算法相对是透明的,不是基于训练的黑盒算法,所以应用范围也十分广。
原文地址