强化学习(九)--策略梯度

之前咱们的介绍解决的是当值状态接近于无限或者连续的时候采用DQN方法，下面我们来想另一个场景，如果我们的动作空间无限大或者连续呢，是不是基于值函数的迭代就不是那么适用啦，这就是本章要介绍的随机梯度策略。
这个时候我考虑将策略参数化，利用线性函数或者非线性函数表示策略，就是 $π_{\theta}(s)$ 以寻找最优的参数 $\theta$ ，使得累计回报最大 $E[\sum R(s_t)|π_{\theta}]$ 最大，这就是策略搜索算法。
除了适用于连续空间场景外，相比较与值函数方法，策略梯度方法还有如下优点。
1.策略搜索梯度方法具有更好的收敛性
2.策略搜索方法更加简单。在某些情况下，使用基于值函数的方法求解最优策略十分复杂甚至无效。
3.策略搜索方法可以学到随机策略。

确定性策略指给定状态s，动作唯一确定

π_{\theta}(s)=a

随机策略是指状态s下，动作符合一个概率分布。

π_{\theta}(a|s)=P(a|s;\theta)

如下这样的格子世界，避开骷髅的情况下最快的找到钱袋，最优策略如果是一个确定策略的话，是不是会出现一些问题。假设我们使用东南西北方向是否碰壁作为特征表示格子的状态，我们会发现，两个灰色格子是完全相同的（使用周边格子描述当前位置的状态S一致）。
之后我们会学到如下的策略

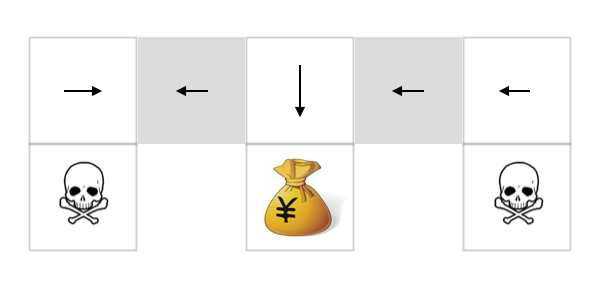
在灰色格子上往复运动不能出来。这种情况我们成为发生了状态重名。这个时候随机策略会优于确定性策略。

π_{\theta}(wall to N and S,move E) =0.5 \\ π_{\theta}(wall to N and S,move W) =0.5 \\

之前我们的理论告诉我们，对于任意一个MDP总有一个确定性的策略，不过那是针对状态可完美预测或者使用特征可以完美描述状态的情况。
当然策略搜索方法也有一些缺点，如在使用梯度法对目标进行求解的时候，容易收敛到局部最小值。

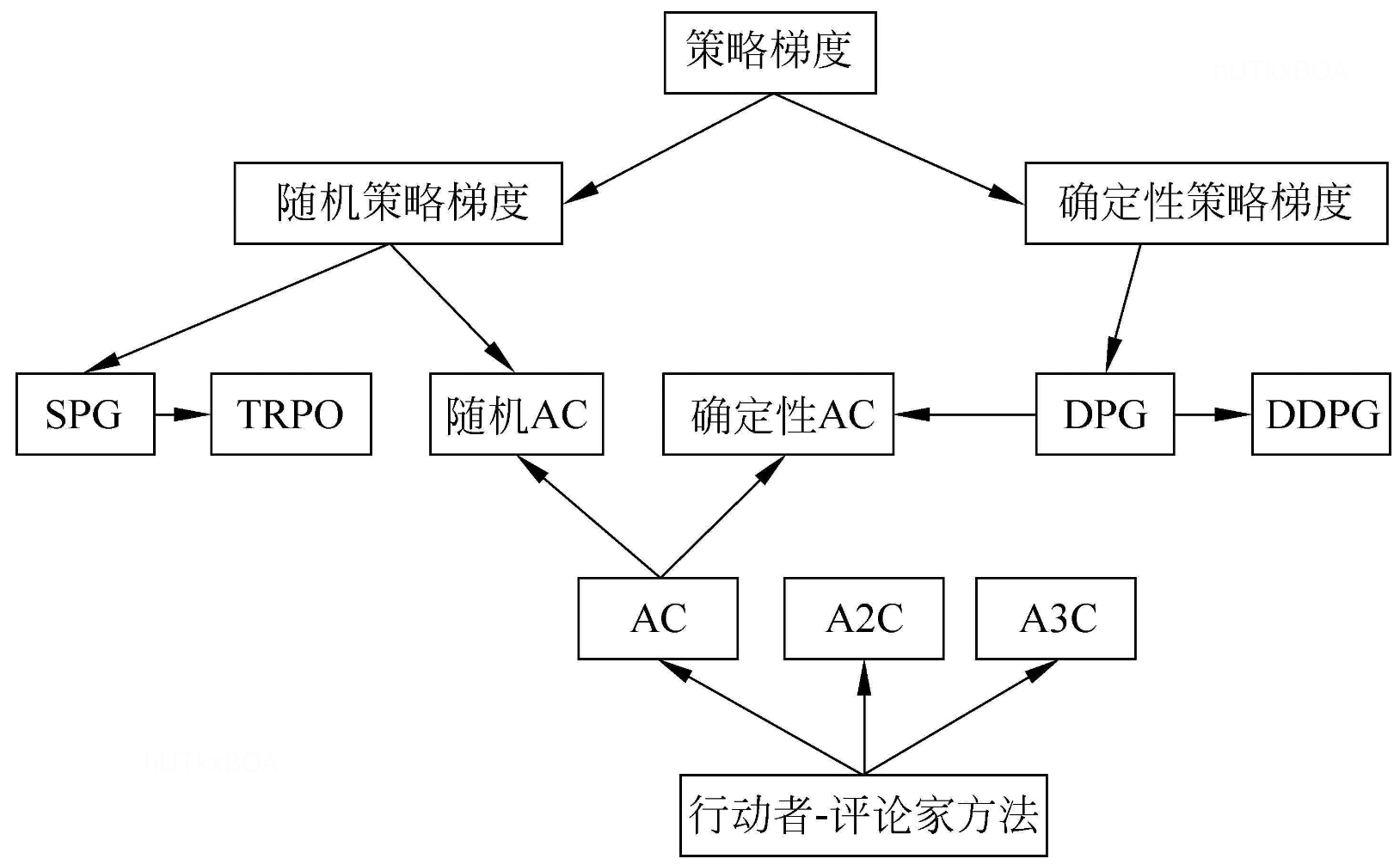
策略梯度的分类

根据策略是随机策略还是确定性策略，分为随机策略梯度和确定策略梯度。随机策略梯度存在学习率难以确定的问题，就有了置信域优化（TRPO），它能够确定一个使得回报函数单调不减的最优步长。确定性策略方法使用的是线性函数逼近和非线性函数逼近。
在这章之前我们接触的强化学习都是使用广义的策略迭代框架，它包括两步，策略评估和策略改进。本章我们介绍一种全新的框架，行为者-评论家(AC)框架，评论家用来对行为值函数进行更新，行动者根据更新后的行为值函数对策略函数参数进行更新。
根据采用策略的不同，可以分为随机行为者-评论者方法和确定性行动者-评论者。如果用优势函数代替行为值函数，评论家直接对优势函数的参数进行更新，就有了优势行为者-评论者（A2C）。如果进一步，在进行行为探索时，同时开启多个线程，每个线程相当于一个智能体，多个智能体共同探索，并行计算策略梯度，维持一个总量的更新。就有了异步的行为者-评论者(A3C).

策略关系图

蒙特卡洛策略梯度

REINFORCE算法

这里的策略是一个关于 $\theta$ 的函数，中间的关于 $\theta$ 的一个迭代公式可以由策略梯度定理获得，这里就不给出详细推导过程啦。REINFORCE是要求有完整轨迹的方法，所以这里是属于蒙特卡洛一类的方案。

TRPO

TRPO是信赖域策略优化的简称，属于策略梯度算法的一种。策略梯度算法在连续领域取得了一些成就，但是也遇到一些问题。

很难选择合适的更新步长，由于策略是不断变化的，输入数据也是不是固定的，会导致回报的分布变化。所以很难在变化中选择一个固定的步长。

TRPO解决的问题就是如何选择一个合适的补偿，找到新的策略使得回报的函数值增加。

TRPO算法

为了解决这个问题，一个很自然的想法就是能不能把新的策略下的预期回报表示为旧的策略下的预期回报加上一个余项，让这个余项大于0，就能保证更新一个更好的策略。令 $\phi(\pi)$ 为在策略π下的预期回报。如公式1.1

\phi(\pi)=E_{s_{0},a_{0}}[\sum_{t=0}^{\inf} \gamma^{t} r(s_{t})] \tag{1.1}

其中π‘表示新的策略，π表示旧策略，那么新的策略的累积回报就可以表述为

\phi(\pi')=\phi(\pi)+E_{s_{0},a_{0},π'}[\sum_{t=0}^{\inf} \gamma^{t} A_{π}(s_{t},a_{t})] \tag{1.2}

其中 $E_{s_{0},a_{0},π'}[]$ 表示动作从新的策略分布 $π'(·|s_{t})$ 中采样得到的。其中

A_{π}(s_{t},a_{t})=Q_{π}(s,a)-V_{π}(s)=E[r(s)+V_{π}(s')-V_{\pi}(s)] \tag{1.3}

其中 $A_{π}(s_{t},a_{t})$ 叫做优势函数，用来评价当前动作相对于平均值的大小，如果 $A_{π}(s_{t},a_{t})>0$ 说明比当前状态更好。进一步展开

\phi(\pi')=\phi(\pi)+\sum_{t} \sum_{s} P(s_{t}=s|π') \sum_{a}π'(a|s)\gamma' A_{π}(s,a) \tag{1.4}

进一步变形

\phi(\pi')=\phi(\pi)+ \sum_{s} \rho_{π'}(s) \sum_{a} π'(a|s) A_{π}(s,a) \tag{1.5}

其中 $\rho_{π'}(s)$ 表示折扣访问频次。

\rho_{π'}(s)=P(s_{0}=s)+\gamma P(s_{1}=s)+\gamma^{2}P(s_{2}=s)+... \tag{1.6}

如何判断一个策略已经达到了最优策略呢？对于等式 $π'(s)=argmax A_{π}(s,a)$ ，如果至少一对状态-动作的优势函数等于0，并且状态访问概率不为0，那么就达到了最优策略，否则就不是最优策略。

重要性采样

为了提升对于数据的利用率。TRPO采用了重要性采样的策略。所谓的重要性采样就是使得和环境交互的策略与要更新的策略不是同一个策略，这样通过和环境交互获得采样数据能够被多次应用到新策略的更新中。

L_{π'}=\phi(π)+E_{a \in π} [\frac{π'(a|s_{n})}{π((a|s_{n}))}] A_{π}(s,a) \tag{2.1}

其中 $L_{π'}$ 和 $\phi(π)$ 的唯一区别是状态分布不同，事实上 $L_{π'}$ 是 $\phi(π)$ 的一阶近似。因此旧策略附近，能够改善L的策略也能改善 $\phi$ 。下一步的核心问题就是更新步长怎么选，引用一个重要的不等式

\phi(π')>=L_{π'}-CD_{KL}^{max}(π,π') \tag{2.2}

其中 $C=\frac{2 \alpha \gamma}{(1-\gamma)^{2}}$ , 而 $D_{KL}^{max}$ 为每个状态下动作分布的散度的最大值，也可以使用平均散度，最终希望找到参数 $\theta$ 满足 $max_{\theta}[L_{\theta_{old}}-CD_{KL}^{avg}(\theta_{old},\theta)]$ , 其中 $\theta$ 表示新策略的对应参数， $\theta_{old}$ 表示旧策略对应参数。

伪代码

TRPO算法

使用场景

策略梯度的缺点就是数据使用效率以及鲁棒性不好。TRPO方法又比较复杂且不兼容dropout和参数共享。后面咱们进一步介绍近端策略优化算法，更容易实现且效率更好。
TRPO方法通过使用了约束而非惩罚项的方式保证策略更新的稳定性，主要原因是作为惩罚项的引入十分难调节参数。所以也一般不建议使用TRPO算法。

支付宝捐赠