动态规划
动态规划相信大家都是了解的,这是一个运筹学的分支,其核心的思想是将一个大的问题分解成n个小问题,而要解决这个大问题,往往需要这些小问题的解,一般通过某些方式存储起来,从而节省大量时间。
而马尔可夫就具有这样的特性,所有动态规划经常被用作解决强化学习问题的方法。
策略评估
我们在做强化学习的同时往往要解决一个问题就是策略评估,也就是当给你一个策略π如何来计算该策略的值函数Vπ,因为实际中设计到的模型规模比较大,因此需要迭代的求解。我们来回顾下贝尔曼方程。
Vπ(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′aVπ(s′))(3.1)
可见,状态s处的值函数可以利用后继的状态s‘的值函数表示,这种求解方式叫做自举法。
初始的所有值函数如果为0,第k+1次迭代和求解Vπ(s),需要使用第k次的算出来的值函数。Vk(s′),所以它的迭代公式应该是
Vk+1(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′aVk(s′))(3.2)
对于模型已知的强化学习算法,上式中的Pss′a,π(a∣s),Rsa是已知的。
策略改进
通过前几节的学习,我们能知道,计算值函数的目的就是想利用值函数找到最优策略。通过上面的方法能够获得值函数,那么如何使用值函数进行策略的改进就是本章要讲解的重要内容啦。直觉上很容易想到
πl+1(s)=∈argsmax Qπl(s,a)(3.3)
而
Qπ(s,a)=Rsa+γs′∈S∑Pss′aVπ(s′))(3.4)
在当前策略π的基础上,利用贪心的选取行动,直接将所选择的动作改变为当前的最优动作。
下面我们来说一段绕口令啦,当动作改变后对应的策略为π’,a’在状态s下遵循π’选取的动作,同理a’'为在状态s’下遵循π’选取的动作。改变动作的条件是Qπ(s,a′)>=Vπ(s).可见值函数对于策略每一点改进都是单调递增的。因此对于策略π,可以放心的改进
π′=maxQπ(s,a)(3.5)
策略迭代
讲完前两部分其实策略迭代十分简单,实际上就是策略评估和策略改进的交互过程啦。这里我们就不多讲这个问题。
我们来看看伪代码
伪代码开始
输入:MDP五元组<S,A,P,R,γ>
初始化值函数V(s)=0,初始化策略π1为随机策略
LOOP
for k =0,1,2,…
V′(s)=a∈A∑π(a∣s)(Rsa+Pss′aVπ(s′))
if V’==V
end if
end for
π′(s)=argmaxQ(s,a)
if π′(s)=π(s)then
break
else π=π’
end if
end loop
伪代码结束
值迭代
通过上面的算法的了解,我们能够看出,策略迭代在每次进行策略迭代的时候,采用的是贝尔曼方程更新值函数,而本节要介绍的值迭代是利用贝尔曼方程直接用行为回报最大的值来更新原来的值。值迭代可以看成是每次值函数的改进。
假设我们在初始的值函数V1(s),基于当前的状态,我们有多个可选动作a。每个动作会引发一个立即回报Rsa,一个或者多个转移。如从s转移到s’,不同的状态s’应有不同的值函数V1(s′),整个的Rsa+γ∑s′∈SPss′aV1(s),称为a的行为回报,值迭代算法直接使用所有的行为引发的行为回报中的取值最大的那个值来更新原来的值,得到V2(s).知道值函数收敛。
策略迭代的例子
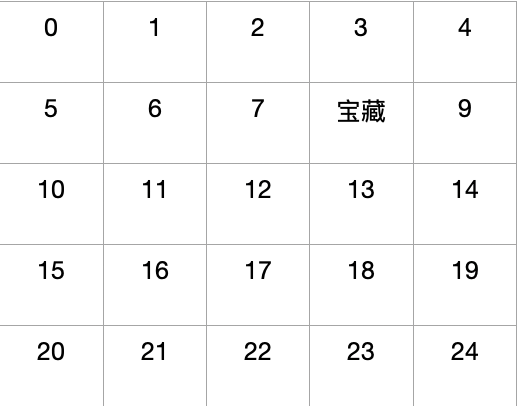
本节我们来举个例子,看看这个例子,如何进行策略迭代的。
我们来描述一下上下问,S∈<0,...,24>,其中状态8是宝藏,动作空间A∈{up,dowm,left,right},宝藏回报r=0,其他位置回报r=-1,当智能体处于边缘位置的时候,智能体的回报为-1,且回到原来的位置,转移概率Pss′a=1,折扣因子γ=1,求解找到宝藏的最优策略。初始策略为随机策略。
π(up∣∗)=0.25
π(down∣∗)=0.25
π(left∣∗)=0.25
π(right∣∗)=0.25
策略迭代公式3.2
那么我们来看看迭代的过程是如何计算的。
初始策略下值函数为V0π(s)如下。
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
第一次迭代k=1,V1π(s)如下。
| -1 |
-1.25 |
-1.3125 |
-1.328125 |
-1.33203125 |
| -1.25 |
-1.625 |
-1.734375 |
0 |
-1.333007 |
| -1.3125 |
-1.734375 |
-1.867187 |
-1.46679688 |
-1.69995117 |
| -1.328125 |
-1.765625 |
-1.90920312 |
-1.84375 |
-1.88592529 |
| -1.33203125 |
-1.77441406 |
-1.9206543 |
-1.94110107 |
-1.95675659 |
我关键来看看如何进行的这第一次迭代。
首先我们来看看s0位置的-1是如何来的。
根据上面的公式3.2
V(s0)=0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1+0)=−1
很明显,在这个位置向周围任意位置移动收益都是-1,且值函数都是0,只有策略转移概率0.25可以用。
这个比较简单,咱们来看看s1,是怎么计算的,这个时候我们是知道s0=-1.
V(s1)=0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1−1)=−1.25
在这个位置除了知道s0的值函数为-1,其他位置仍然是不知道的。所以left方向的计算方法有变,其他没有变化,我们顺便看看s2如何计算。
V(s2)=0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1+0)+0.25∗(−1−1.25)=−1.3125
通过这样的迭代,慢慢这个矩阵得到收敛。
通过公式获取相应的策略
π∗(a∣s)=argsmaxRsa+γs′∈S∑Pss′aV∗s′
| right |
right |
right |
down |
left |
| right |
right |
right |
0 |
left |
| right |
right |
up |
up |
up |
| up |
up |
up |
up |
up |
| up |
right |
up |
up |
up |
算到这里还是没有结束,我们刚刚得到一个策略1,接下来使用贝尔曼方程改善策略1,得到策略2,直到策略收敛,我们才获取一个稳定的策略。方法与上面方法类似,这里就不做过多的解释啦。
值迭代例子
在进行一次策略评估以后,进行策略改进,这种方法叫做值函数的迭代。即每次进行值函数计算时,直接选择哪个使得这个值函数最大的行为。接下来我们来看这个例子。
初始状态不变,所有的状态都是0.
我们来看看第一次迭代的结果。
Vk+1(s)=maxa∈A(Rsa+γs′∈S∑Pss′aV∗s′)(3.6)
| -1 |
-1 |
-1 |
-1 |
-1 |
| -1 |
-1 |
-1 |
0 |
-1 |
| -1 |
-1 |
-1 |
-1 |
-1 |
| -1 |
-1 |
-1 |
-1 |
-1 |
| -1 |
-1 |
-1 |
-1 |
-1 |
我们看看s0的-1是怎么计算的。
根据公式计算
max([−1+0])=−1
转移到四个方向的收益都是-1,转移概率是1,V*都是0.
那么s1呢?
唯一一点不同就是知道了s0=-1,但是带入计算公式发现计算的值更小,所以还是取相对较大的-1,所以以此类推其他的值都是这么算的。
进行了几次迭代以后,我们发现这个矩阵收敛啦。策略也就是确定了。看样子是比我们原来的方案简单很多的。
策略迭代宏观的讲解了策略优化的方法,本文主要介绍如何探索环境也是一个强化学习需要解决的问题,不同的策略其实对环境学习的态度是不一样的。
探索策略
随机策略
随机策略是一个典型的策略,通俗的讲就是在不同的状态下随机采用不同的动作,所以对于随机策略来讲,是一个一直在探索的过程,而这样的探索过程实际上是不断的获取信息,但是不利用信息。工作中也经常遇到这样的人,遇到一个新的项目,不断的探索前沿工作,就是不落地。
显然这种策略并不是一个好的策略。
σ贪心
σ贪心就是一个比较有意思的策略,在利用底层数据上,σ贪心的策略是通常是贪心的,但是偶尔也会随机探索,手机额外的信息。这类策略的表示也很简单,就是经常状态下是选择最大的值函数,但是仍然会有σ的概率选择一个随机动作,这样一来,动作-值函数就有希望收敛到真实的值。
衰减σ贪心
衰减σ贪心的表现形式,在早期智能体对环境体验不够的时候,就是希望能够探索环境,所以σ得之会比较大,随着智能体更好的估计值函数,就希望利用更多的信息,这个时候σ就会变小,探索的概率变小,利用时候变多。也是一种获得真实值函数的方法。
乐观初始化策略
乐观初始化策略的原理十分简单,就是开始的时候将Q值初始化一个很高的值,并利用这些估计值执行贪婪动作,这样随着不断的交互会将这个很高的值逐渐正常化。
还有一些策略型的更新策略,可以看推荐搜索之bandit算法