马尔可夫决策过程提供了基本的理论框架，几乎所有的马尔可夫学习问题都可以使用MDP的决策过程建模。

而本节讲的贝尔曼方程是马尔可夫决策过程用到最基础的方程。贝尔曼方程方程也被称为动态规划方程，贝尔曼方程表达了当前值函数（或行为值函数）和它后继值函数的关系，以及值函数与行为函数之间的关系。而贝尔曼最优方程表达的是当前最优值函数和它后继最优值函数的关系，以及最优值函数和最优行为值函数之间的关系。听起来十分绕，不过咱们慢慢往下讲就可以了解这些内容。

最优策略策略的表示

状态-值函数（有何期望）

状态-值函数是表达每个状态下的值函数，物理含义是当处于状态S下，未来的预期收益应该是多少？
$$ \begin{align*} & V_{\pi}(s)=E_{\pi}[G_t|S_t=s] \\ & =E_{\pi}[R_{t+1} + \gamma R_{t+2}+...|S_{t}=s] \\ & =E_{\pi}[R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3})|S_{t}=s] \\ & =E_{\pi}[R_{t+1}+\gamma G_{t+1}|S_{t}=s] \\ & =E_{\pi}[R_{t+1} + \gamma V(S_{t+1})|S_{t}=s] \\ \end{align*} $$
除了上面的表达，还可以有另一种表达

$$ V_{\pi}(s)=\sum_{a \in A} π(a|s) \sum_{s',r}p(s',r|s,a)[r+\gamma v_{π}(s')] \tag{1.1} $$
π表示一种策略，给定状态s，就给出动作a，p表示给定状态s和a，转移到s'获得收益r的概率，r表示即时收益，$\gamma v_{π}(s')$表示未来收益的加权和。

这里的状态-值函数通常被称为值函数。

动作-值函数(这样做，有何期望)

需要经常考虑的一个关键问题不仅仅是值函数问题，另一个描述的方式是当处在状态s的情况下选择动作的值函数的大小决定在当前状态下采取什么动作。
通过比较同一个策略下的不同动作，就可以选择更好的动作，从而改进策略。当我们关心改进策略的时候，我们就需要动作-值函数。可以进一步思考一下，对于值函数的学习，更多是静态环境的捕捉，但是对于相对的动调环境，就需要 动作-值函数捕捉环境的动态，进而改进策略。动作值函数的表达如下公式1.2

$$\begin{gather}q_{π}(s,a)=E_{π}[G_{t}|S_{t}=s, A_{t}=a] \\ =E_{π}[R_{t}+\gamma G_{t+1}|S_{t}=s, A_{t}=a] \\ =\sum_{s',r}p(s',r|s,a)[r+\gamma v_{π}(s')] \tag{1.2}\end{gather}$$
公式1.2的最后一行也是动作-值函数的贝尔曼方程的定义。

动作优势函数（如果这样做，有什么进步）

另一种值函数是有前两种值函数演变过来的。又称为优势函数，使用$a_{π}(s,a)$,是指动作a在状态s中的动作-值函数与策略π下的状态s的状态值函数之差。

$$ a_{π}(s,a)=q_{π}(s,a)-v_{π}(s) \tag{1.3} $$

状态转换

接下来我们来看看状态值函数和动作值函数之间的关系。

基于状态s，采取动作a求$V_{\pi}(s)$

在遵循策略$\pi$的情况下，状态s的值函数体现在该状态下采取所有可能行为值函数$Q(s,a)$为行为发生概率$\pi(a|s)$的乘积之和。
$$ V_{\pi}(s)=\sum_{a \in A} \pi(a|s) Q_{\pi}(s,a) \tag{2.2} $$

采取行动a，状态转换为s'，求取$Q_{\pi}(s,a)$

$$ Q_{\pi}(s,a)=R_{s}^{a}+\gamma \sum_{a \in A} P_{ss'}^{a} V_{\pi}(s') \tag{2.3} $$

基于状态s，采取行动a，转为状态s’，求取$V_{\pi}(s)$

$$ V_{\pi}(s)=\sum_{a \in A} \pi(a|s)(R_s^a + \gamma \sum_{s' \in S} P_{ss'}^{a} V_{\pi}(s'))\tag{2.4} $$

采取行为a，状态转变为s‘，采取行动a’，求$Q_{\pi}(s,a)$

$$ Q_{\pi}(s,a)=R_{s}^{a}+\gamma \sum_{s' \in S} P_{ss'}^{a} \sum_{a \in A} \pi(a'|s')Q_{\pi}(s',a') \tag{2.5} $$

是不是太复杂啦，咱们还是举个例子来看看在实际的转移关系中怎么来算这些值。

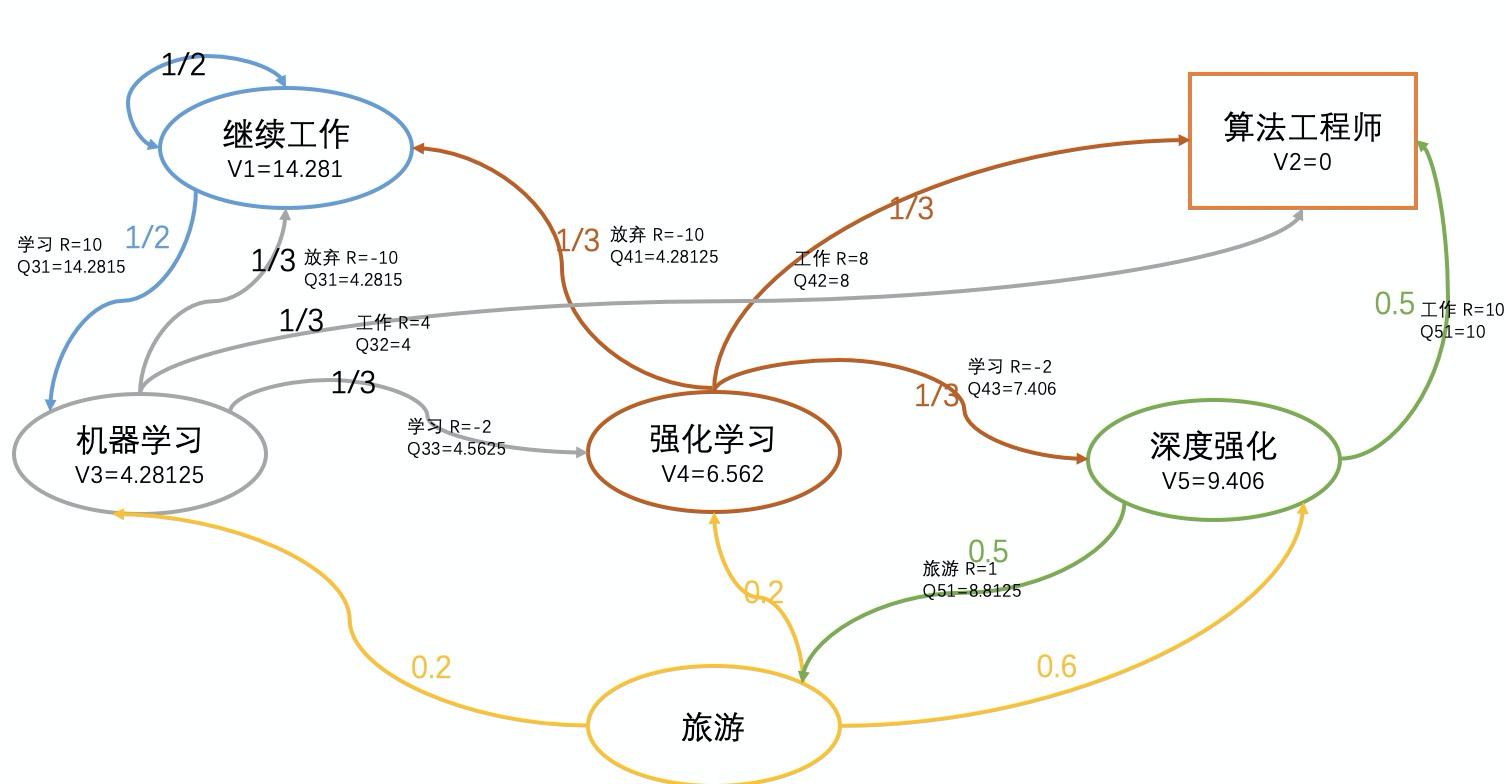
我们先来看看$V_{\pi}(s)和V_{\pi}(s‘)$的关系，假设选择强化学习，那么对应值函数$V_4$表示当前状态值函数，$V_4$的后继值函数分别是$V_1,V_2,V_5$。已知$V_1,V_2,V_5$

$$ V_{4}=\frac{1}{3}[(-10+1 \times 1 \times V_{1}) + (8+1 \times 1 \times V_{2}) + (-2 + 1 \times 1 \times V_{5})]=6.56 $$

上面公式可以对应公式2.4的 $'$\gamma$'$和$'$P_{ss'}^{a}$'$.类似的大家可以验证以下其他的关系。

贝尔曼最优方程

贝尔曼最优方程表达是当前状态的最优值函数和后继的最优值函数的关系。

$$ V^{*}(s) = max\ V_{\pi}(s) \tag{2.6} $$

$$ Q^{*}(s,a) = max\ Q_{\pi}(s,a) \tag{2.7} $$

基于状态s采取行动a，求$V^{*}(s)$

当前状态的值函数$V^{*}(s)$等于从该状态s出发，采取所有行动中对应的那个最大行为值函数

$$ V^{*}(s) = max\ Q^{*}(s,a) \tag{2.8} $$

采取行动a，状态转变为s‘，求取$Q^{*}(s,a)$

在某个状态下，采取某个行为的最优价值$Q^{*}(s,a)$有两部分构成，一部分是离开状态s立即回报$R_{s}^{a}$，另一个部分是能够到达s’的最优状态价值$V^{*}(s)$出现概率的总和。

$$ Q^{*}(s,a) =R_{s}^{a}+ \gamma \sum_{s' \in S} P_{ss'}^{a} V^{*}(s') \tag{2.9} $$

基于状态s，采取行动a，状态转变为s‘，求$V^{*}(s)$

$$ V^{*}(s) = max\ R_{s}^{a} + \gamma \sum_{s' \in S} P_{ss'}^{a} V^{*}(s') \tag{2.10} $$

采取行动a，状态转变s’，采取行动a‘，求$Q^{*}(s,a)$

$$ Q^{*}(s,a) =R_{s}^{a}+ \gamma \sum_{s' \in S} P_{ss'}^{a} max Q^{*}(s',a') \tag{2.11} $$

最优策略

讲到这里，强化学习的基本理论就差不多啦，我们来回头看看强化学习的形式化描述。$M=<S,A,P,R,\gamma>$，这里我们就不一一介绍啦，之前应该都介绍过每个符号的意义。这里介绍两个新的概念。T为总的时间步，$\tau$叫做轨迹序列，$\tau=(s_0,a_0,r_0,s_1,a_1,r_1....)$,对应的累积回报为$R=\sum_{t=0}^{T}\gamma^{k} r_t$。那么强化学习的目标就是找到最优的策略$\pi$，该策略累积回报期望最大。说着这么大一堆，是不是了解强化学习要解决个什么问题呢？

求解最优策略

当值函数最优的时候，采取的策略也是最优的，反过来策略最优的时候值函数也是最优的，这个叫做策略最优定理，所以可以通过求解最优的值函数$V^{*},Q^{*}$来求解最优策略。

一旦我们知道了$V^{*}$，基于每个状态s，做一步搜索，搜索以后出现的最优的行为将会是最优的。

同理我们如果有最优的值函数$Q^{*}$,求解最优策略就更好了，只要找到最优的状态就可以啦。

综上所述

我们来总结一下，本节主要讲的就是贝尔曼方程，以及最优策略，最优值函数等。