之前的学习中,我们了解到学习强化学习的数据是完整的采样轨迹(蒙特卡洛方法),使用动态规划需要采用自举的方法,使用后继的值函数估计当前的值函数,本章要介绍的实际上是这两种方法的结合,叫做时序差分。
我们首先来回顾一下原来值函数的估计方程。
V(st)<−V(st)+α(Gt−V(st))(5.1)
而时序差分的场景是不完整的轨迹,无法获取累计回报。它在轨迹st的值函数的时候,用的是离开该状态的立即回报Rt+1,与下一个状态的St+1的预估折扣值函数γV(St+1)之和来估计。至于这段的理论基础在哪里呢?实际上是1988年Sutton首次证明了时序差分的最小均方误差上的收敛性。之后时序差分就应用到无法产生完整轨迹的无模型强化学习上。
那么它的公式就变成如下的样式
V(st)<−V(st)+α(Rt+1+γV(St+1)−V(St))(5.2)
其中Rt+1+γV(St+1)称为TD(时序差分)的目标值;Rt+1+γV(St+1)−V(St)称为TD的误差
蒙特卡洛、动态规划和时序差分的对比
首先三种方法的核心不同点体现在值函数的更新公式上,蒙特卡洛(MC)方法使用的是值函数的原始定义,该方法依靠采样的完整性上,利用实际的累计回报平均值Gt来轨迹值函数,
TD和DP则是利用一步预测的方法计算当前状态值函数,其共同点就是利用的自举,使用后继的值函数逼近当前的值函数。不同的是DP无须采样,直接根据完整模型通过当前的状态S所有可能的转移状态S’,转移概率,立即回报来计算当前状态的S的值函数。而TD方法是无模型方法,无法获取当前状态的所有后继回报和状态,仅能通过采样学习轨迹片段用下一个状态的预估状态更新当前状态的预估价值。
这里也给出一个总结。

方差和偏差的对比
这里我们通过方差和偏差两个角度来对比这三种方法,对于MC算法来讲,因为采用的大量的模拟轨迹,使用累计回报的策略,每次的动作随机性较大,所以期望等于真值,但是方差却极大。
TD算法使用的是目标函数,是基于下一个状态的真值和当前状态的真值做对比,所以TD的估计是一个无偏估计,但是实际应用中,是基于下一个状态的值函数计算当前预估的值函数,因此是一个有偏估计,但是和MC相比,TD只用了一步随机状态和动作,因此随机性会小很多,方差也会小很多。
| 方法 |
偏差 |
方法 |
| DP |
无偏差 |
无方差 |
| MC |
无偏差 |
无方差 |
| TD |
无偏(真实TD目标),有偏(预估TD目标) |
低方差 |
马尔可夫性质
DP的方法是基于模型的方法,基于现有的一个马尔可夫决策模型的状态转移概率和回报,因此具有马尔可夫性质。
而MC和TD都是无模型方法,需要通过轨迹估计当前的状态值函数,不同的是TD不需要完整的轨迹,利用现有的模型构建一个最大可能的马尔可夫决策模型。所以TD也具有马尔可夫性。而MC是一个纯粹的概率模拟,所以不具有马尔可夫性。
Sarsa:在线策略TD
与前面讲到的方法一直,TD也分为策略评估和策略改进两个步骤。根据产生的采样数据的策略和评估改进的策略是否为同一套策略,可以分为在线策略和离线策略。
本节要讲的就是在线策略。我们来简单描述一下这个过程。
基于状态S,遵循当前的策略π,选择一个动作A,形成了一个状态行为(S,A),与环境交互,得到回报R,进入下一个状态S’,再次遵循当前策略,产生一个行为A’,产生第二个状态行为(S’,A’),利用后一个状态行为对(S’,A’)的Q(S’,A’)值更新前一个状态行为(S,A)的Q(S,A).
Q(S,A)<−Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))(5.3)
Q-learning:离线策略TD
离线的策略TD学习任务是借助策略μ(a∣s)的采样数据来评估另一个策略π(a∣s).
离线策略TD也使用重要性采样,假设状态st遵循两个不同的策略产生同样的动作a,那么两种情况产生的行为at的概率是不一样的。
首先我们考虑使用策略π来评估策略π。基于状态st,遵循状策略π,产生行为at,得到回报Rt+1,进入新的状态st+1,再次使用策略π,产生行为at+1,评估策略π对应的目标TD为
Rt+1+γQ(st+1,at+1)(5.4)
如果改用策略μ来评估策略π,就需要给Rt+1+γQ(st+1,at+1)乘以一个重要性采样,对应的TD目标变为。
μ(at∣st)π(at∣st)(Rt+1+γQ(st+1,at+1))(5.5)
所以离线策略的TD对应的数学表达为
Q(st,at)<−Q(st,at)+α(μ(at∣st)π(at∣st)(Rt+1+γQ(st+1,at+1)−Q(st,at)))(5.6)
这个公式我们可以这样理解,在状态st的时候,分别比较策略π(at∣st)和当前策略μ(at∣st)产生at的概率大小,比值作为TD目标的权重,依次调整原来的状态st的价值Q(st,at).
应用这种思想就是Q-learning方法。它的一个要点就是,更新一个状态行为对的Q值,采用的不是当前策略的下一个状态行为对的Q值。
Q(St,At)<−Q(St,At)+α(Rt+1+γQ(st+1,A′)−Q(St,At)))(5.7)
TD的目标Rt+1+γQ(st+1,A′)是基于目标策略π产生的行为A’得到的Q值和一个立即回报的和。在Q-learning方法中,实际与环境交互的遵循策略μ是一个基于原始策略的σ贪心策略,目标策略π是单纯的贪心策略。
同Sarsa方法一样,Q-learning的具体执行时,单个轨迹内,每执行一个时间步,也会基于这个时间步的数据对行为值函数进行更新。其中产生的采样策略是σ贪心,而评估改进的策略是贪心策略。
在线策略和离线策略
这里咱们来对比一下在线策略和离线策略, 在线策略是说行为策略和目标策略是同一个策略,而离线策略是说行为策略和目标策略不是同一个策略。 Sarsa算法是典型的在线策略,Q-learning是离线策略。
- 对于sarsa算法。它的更新公式必须使用当前策略采样的到(s,a,r,s’,a’),因此它是在线策略
- Q-learning,它的更新公式是四元组(s,a,r,s’)来更新当前状态动作对的动作价值Q(s,a),数据s和a是给定的条件,r和s’是采样的到的,这个四元组不一定是当前策略采样的到的。
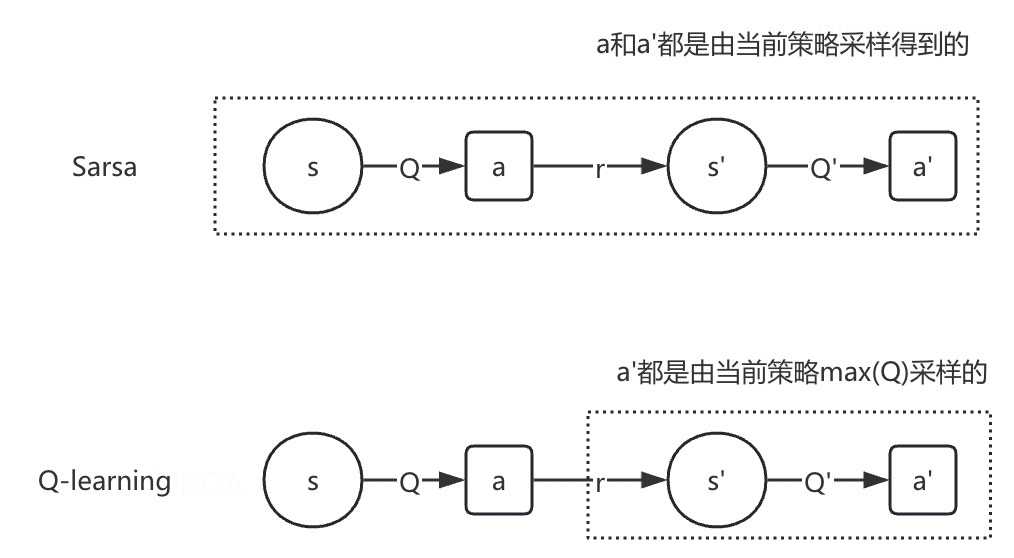
SARSA与Q-Learning的核心区别在于策略更新机制:SARSA采用on-policy策略,基于当前策略选择的下一个动作更新Q值;而Q-Learning采用off-policy策略,直接使用下一状态的最大Q值进行更新