贝叶斯网络一般是指带有概率信息的有向无环图。贝叶斯网络的信息有两部分组成。首先是表示独立信息的一个网络结构S，S中每个节点表示特定域中的一个概念或者变量，节点间的弧表示了可能的因果关系，体现了域知识的特征。其次每个节点都负有一个与该变量相联系的概率分布函数(CPD)， 如果概率是离散的，那么在给定了父母节点的时候取不同值的条件概率表(CPT).CPT体现了域知识的定量方面的特征。可见，贝叶斯网络是一种表示数据变量之间潜在关系的定性定量的方法，它使用这种图形结构指定了一组条件独立的声明和用于刻画概率依赖强度的条件概率，如图1所示。
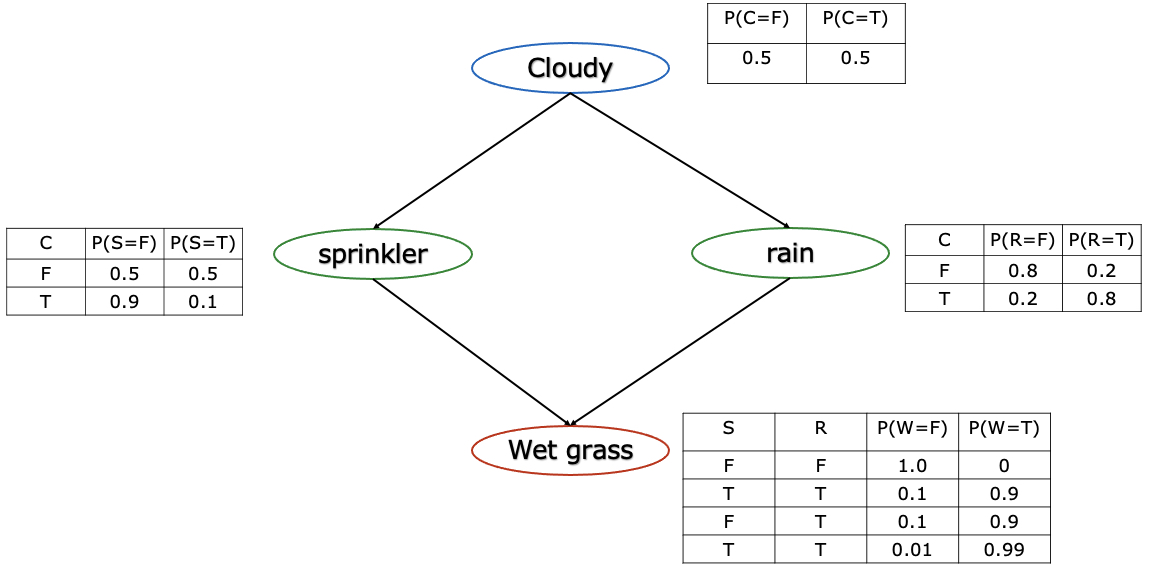
贝叶斯网络表达
下面就要形式化的表达一下贝叶斯网络。假如有一组有限集合$(Y_{1},...,Y_{n}($表示一组离散的随机变量，取值分别是$(y_{1},...,y_{n})$的联合概率为
$$
P(y_{1},...,y_{n})=P(y_{n}|y_{n-1},..,y_{1})...P(y_{2}|y_{1})P(y_{1})=\prod P(y_{i}|y_{i-1},...,y_{1}) \tag{1.1}
$$
在贝叶斯网络中，使用条件独立构造知识以后，就能将公式1.1简写成如下的形式
$$
P(y_{1},...,y_{n})=\prod P(y_{i}|Pa(y_{i}))
$$
其中$Pa(y_{i})$是节点$y_{i}$的父节点组。当它们的取值一定的时候，可见联合概率空间中每个状态都可以通过贝叶斯条件概率的乘积获得。
当贝叶斯作为分类器使用的时候，假设类别空间$C=(c_{1},..,c_{n})$,特征空间为$X=(X_{1},...,X_{n})$每个特征的值域为$Val(X_{i})$，对于某一个实例$x=(x_{1},x_{2},..,x_{n})$来说，分类器的目的是通过学习获得训练样本中D，来获取它的类别标签c，贝叶斯网络分类器采用的表达式为
$$
p(c_{i}|x)=\frac{p(c_{i})\times\prod p (x_{j}|c_{i};\pi(x_{j}))}{p(x)} \tag{1.1}
$$
其中$\pi(x_{j})$为节点$X_{j}$除了类别节点C之外所有的父节点，$x_{j}$为实例x第j个特征的取值，所以贝叶斯网络的分类任务是从训练样本D中学习概率分布$p(c_{i}),p (x_{j|c;\pi(x_{j})})$,这个学习任务分为两个部分，一个是对于每个特征节点找到除类别节点以外的所有父节点，也就是网络的机构。二是在已知的结构上，获取这些参数的估计，也就是参数的学习。接下来介绍几种常见的贝叶斯分类器
朴素贝叶斯网络
朴素贝叶斯分类器是贝叶斯网络中最简单的分类器。它将类别节点作为根节点，其各属性节点相互独立，且都已根节点为父节点。
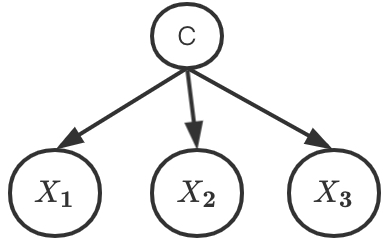
也就是说已知了$X_{1}, ...,X_{n}$求$p(X_{c}|X_{1}, ...,X_{n})$
根据贝叶斯公式
$$\begin{gathered}p(x_{cj}|X_{1}, ...,X_{n})=\frac{p(X_{1}, ...,X_{n}|X_{cj})}{p(X_{1}, ...,X_{n})} \\
=\frac{p(X_{1}, ...,X_{n}|X_{cj}) p(x_{cj})}{\sum_{i=1}^{k} p(X_{1}, ...,X_{n}|X_{cj}) p(X_{cj})} \\
\tag{2.1}\end{gathered}$$
其中$p(x_{cj})$为先验概率， $X_{1}, ...,X_{n}$相互独立，最终化简为如下的形式
$$
p(p(X_{1}, ...,X_{n}|X_{cj})=\prod p(X_{i}|X_{cj})
$$
朴素贝叶斯分类器虽然简单，但是在实际的应用中表现出来的分类能力是不输给C4.5决策树分类器的。然而由于属性间的独立性比较难以获得，实际应用中比较难以满足。
通用贝叶斯网络
通用贝叶斯分类器是将类节点和属性节点作为同等的网络节点，根据数据集中的数据训练贝叶斯网络，直接作为分类器的。用通用贝叶斯分类器进行分类的过程中，实际上是将属性节点作为证据引入到贝叶斯网络中，求得类节点各个取值的后验概率的过程。后验概率最大的时候，类别节点相应的取值。进一步解释，在通用贝叶斯网络中，把某些节点的父节点、子节点以及子节点的父节点称为该节点的马尔可夫覆盖。根据有向马尔可夫覆盖。根据马尔可夫的性质，某个节点各取值的概率只受到有向马尔可夫覆盖节点的影响。
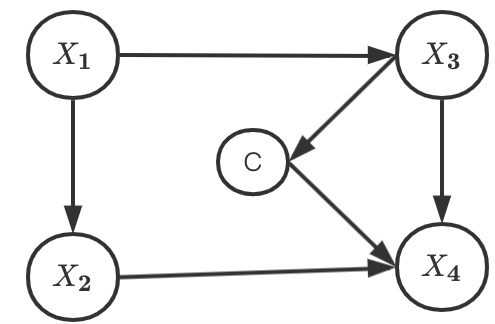
增强型朴素贝叶斯网络
增强型朴素贝叶斯网络（TAN）是朴素贝叶斯网络进行有效改进的分类器，既有朴素贝叶斯分类的简单，又可以有更好的分类性能。
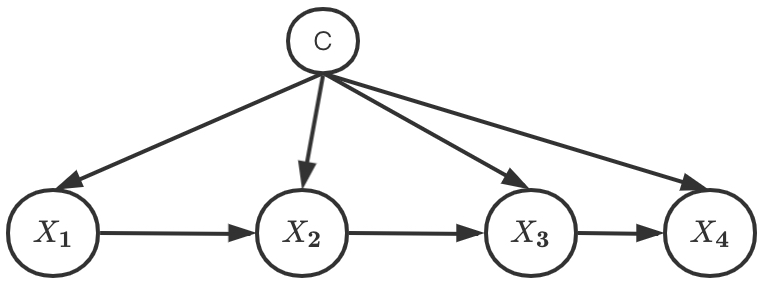
其核心思路是将贝叶斯网络的某些依赖关系的能力和朴素贝叶斯简单性相结合。令$U=(X_{1},...,X_{n},C)$。其中类别变量是C是根节点，而属性节点$X_{i}$除了父节点C以外还有一个父节点$X_{j}$. $Pa(X_{i})=2$.
因此确定了TAN分类模型的结构关键是如何确定每个属性节点的非类父节点，确定属性节点的父节点需要学习算法获取。目前主流的方法有两种
1. 基于分布的构造算法
2. 基于分类的构造算法。
马尔可夫毯贝叶斯网络
马尔可夫毯贝叶斯网络(MBBN)能够表示通用贝叶斯网络分类器中相同的关于类节点的完整马尔可夫毯，尽管通用的贝叶斯网络可以被用来进行分类任务，但是由于根节点没有被特殊对待，有部分节点与类节点并不是直接相关，导致分类的准确准确率不高。另外对于其他朴素贝叶斯分类器中，都假设分类变量是根节点。但是MBBN却没有这种假设，结构表达更加丰富，更加准确的进行因果分析和分类预测。
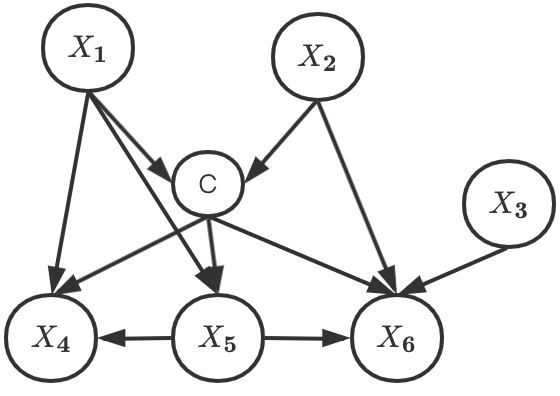
MBBN学习步骤
- 在除了C的节点找到C的父节点集合$z_{p}$，孩子节点集合$z_{c}$和不相关集合$z_{n}$。当父节点因子$\theta_{p}$大于孩子节点因子$\theta_{c}$的时候，加节点$x_{i}$到$z_{p}$,否则到$z_{c}$，当$max(\theta_{p},\theta_{c})<1$则是加入到$z_{n}$。其中
$$\begin{gathered}\theta_{p}=\frac{g(x_{c},\pi_{c} \cup \{x_{i}\})}{g(x_{c},,\pi_{c})} \\
\theta_{c}=\frac{g(x_{i},,\pi_{i} \cup \{x_{c}\})}{g(x_{i},\pi_{i})} \\
g(x_{i}, \pi_{i})=\prod_{j=1}^{q_{i}} \frac{(r_{i}-1)!}{(N_{ij}+r_{i}-1)!} \prod_{k=1}^{r_{i}}N_{ijk}!\end{gathered}$$
其中$\pi_{i}$和$\pi_{c}$表示节点$x_{i}$和$x_{c}$的父节点集合；$r_{i}$表示$x_{i}$的取值数目；$N_{ijk}$是第i个节点取值为第k个值的时候，在父节点取值组合取第j个值数据的数目
- 使用K2算法，在除了$x_{c}、z_{c}$的节点中找到$z_{c}$的父节点
- 使用TAN算法，在$z_{c}$中找到每个节点的另一个父节点。
总而言之
通过上面的介绍，我们知道集中贝叶斯网络的结构，实际应用中往往都是因材施教。此外还会有动态贝叶斯网络等结构，这里就不一一介绍啦，后面的章节中会一步一步的介绍学习结构的算法和学习参数的算法。