之前的章节中咱们已知介绍给定因果图关系以后如何分析图中各个因素之间的关系，对撞路径等等。今天这篇文章中咱们主要介绍一下贝叶斯网络的雏形，开启因果推断的核心区域的探索。

条件独立与图

咱们在训练模型的时候经常会说条件变量独立，或者是独立同分布这样的名词，那么条件独立怎么在因果中使用并且怎么给出一个比较客观的定义呢？
令$V=\{V_{1}, V_{2}...\}$是包含有限个变量的集合。令P(·)是V中变量的联合概率函数，令X、Y、Z表示V中的变量的三个子集。如果

$$P(x|y,z)=P(x|z)$$

P(y,z)>0,那么在已知Z的情况下X和Y条件独立。换句话说一旦知道了Z， 那么获悉Y的值不会帮助获得X的值有任何额外信息。这就是咱们经常说的条件独立,形式化表达为$(X \bot Y | Z)$.且独立一般有如下的性质.或者当P满足$(X \bot Y | Z)$，当且仅当P(X,Y|Z)=P(X|Z)* P(Y|Z).

对称性: $(X \bot Y | Z) \Rightarrow (Y \bot Z | Z)$
分解性： $(X \bot YW |Z) \Rightarrow (X \bot Y |Z)$
弱联合性：$(X \bot YW |Z) \Rightarrow (X \bot Y |ZW)$

收缩性：$(X \bot Y | Z)\& (X \bot W | ZY) \Rightarrow (X \bot YW |Z)$
相关性：$(X \bot W|ZY) \& (X \bot Y|ZW \Rightarrow (X \bot YW |Z)$

不同路径判断独立

链式结构

对于链式结构而言，

$$p(a,c|b)=\frac{p(a,b,c)}{p(c)} \\ =\frac{p(a)p(b|a)p(c|b)}{p(c)} \\ =p(a|b)p(c|b)$$

从而推出a,c关于b独立， $A \bot C|B$

叉式结构

$$p(a,c|b)=\frac{p(a,b,c)}{p(b)} \\ =p(a|b)p(c|b)$$

这种情况存在，A、B不独立，但是关于条件C独立。

对撞结构

如对撞结构可以得出，

$$p(a,b,c)=p(a)p(c)p(b|a,c) p(a,b)=p(a)* p(b)$$

假设观测到了B，

$$p(a,c|b)=\frac{p(a,b,c)}{p(b)} \\ =\frac{p(a)p(c)p(b|a,c)}{p(c)}\\$$

这种情况下， 一般ac在b的条件下不独立，

贝叶斯网络

顾名思义，接下来咱们就要以图的形式来看你研究的问题的各个因素之间的关系啦。
图分为有向图和无向图。无向图一般称为马尔可夫网络，主要是表示对称的空间关系。而有向图一般称为DAG，用于表示因果关系或是时间关系，这种图就可以称为贝叶斯网络。

1. 输入信息的主观属性
2. 依赖贝叶斯条件作为信息更新的基础
3. 区分推理因果模式和证据模型

DAG给出的基本分解方案如下，给定一个定义了n个离散变量的分布P。我们可以将变量任意排列$X_{1},..,X_{n}$，然后P分解成多个概率的乘积。

$$P(x_{1},...,x_{n})= \prod P(x_{j}|x_{i},...,x_{j-1}) \tag{1.1}$$

现在假设某些变量$x_{j}$的条件概率不是对$x_{j}$的所有前期变量敏感，而仅仅对其中一小部分敏感。那么将这部分敏感的前驱变量记为$pa_{j}$，那么公式1.1可以写成

$$P(x_{j}|x_{i},...,x_{j-1}) =P(x_{j}|pa_{j}) \tag{1.2}$$

这样就极大的减少了输入信息。集合$pa_{j}$称为$x_{j}$的马尔可夫父代变量集合，简称父代。

马尔可夫父代变量集合

令$V=\{X_{1},...,X_{n}\}$是有序集合，令P(V)表示这些变量的联合概率分布。如果$PA_{j}$使得$X_{j}$独立于其他所有的前驱变量的极小前驱变量集合，那么变量集合$PA_{j}$称为$X_{j}$的马尔可夫父代集合。形式化的表示为

$$P(x_{j}|pa_{j}) =P(x_{j}|x_{i},...,x_{j-1}) \tag{1.3}$$

$PA_{j}$是满足公式1.3的$\{X_{1},...,X_{j-1}\}$的子集且$PA_{j}$的任何子集合均不满足公式1.3.
根据上面的描述，如何构建一个因果贝叶斯网络图呢？首先对$(X_{1},X_{2} )$进行检测， 当且仅当着两个变量相关时，就画一个从$X_{1}$到$X_{2}$的箭头。继续处理$X_{3}$，若$X_{3}$独立于$X_{1}，X_{2}$，那么不画箭头。否则，检测$X_{2}$是否使得独立于$X_{1}$, $(X_{3} \bot X_{1}|X_{2})$, 或者$X_{1}$是否使得$X_{3}$独立于$X_{2}$。第一种情形，就画一个从$X_{2}$到$X_{3}$的箭头。第二种情况就画一个$X_{1}$到$X_{3}$的箭头，如果没有发现条件独立，就从$X_{2}$和$X_{1}$都画一个箭头到$X_{3}$。

d准则分离

首先咱们来看下面三种场景的因果结构。



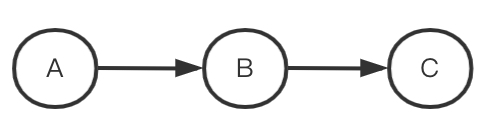
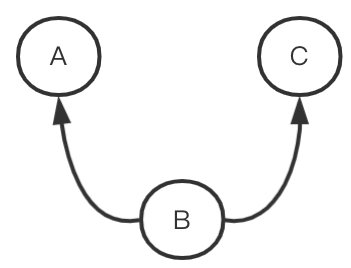
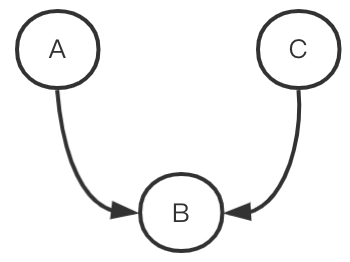
上图分别是链式结构、叉式结构、对撞结构。
链式结构和叉式结构中的A和C相关都是因为B的存在，因此如果B是确定的某一个值，那么A和C就以B为条件独立了就是 $A \bot C | B$, 但是对于对撞结构而言，在对撞结构中A和C是独立的，当B的值确定后，以B为条件，A和C就相关了。

对撞结构的例子

假设A为是否不运动，C为是否吃垃圾食品，B为是否肥胖。
当知道B为肥胖时，如果我们知道A为不运动则可以推断出C为吃垃圾食品，即A和C在条件B下相关。而如果B的答案未知，那么A和C就没有关系，即是否运动和是否吃垃圾食品没有关系。

在因果关系领域，这种判断是否条件独立的方法被称为D-分离。

后门准则

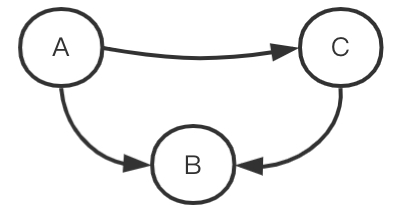
对于上图这种结构，是一种伪相关，消除伪相关的一种方法是采用后门准则，A->C是前门路径， 而A<-B->C是后门路径，后门准则就是将A和C之间的后门路径都阻断，从而得到A和C之间真正的因果关系。是不是感觉被骗啦，这不就是咱们讲过的控制变量B，观察AC之间的因果关系吗？

贝叶斯网络构建的方法

1. 选择变量的一个合理顺序：$x_1,x_2,……x_n$
2. 在网络中添加一个节点$x_{i}$,使之满足$p(x_{i}|parent(x_{i}))=p(x_{i}|x_1,x_2,……x_{i-1})$
3. 如果不相等则说明它们不独立,可以引出一条线,否则它们之间没有联系。
4. 然后增加一点，继续判断，直到结束。

总而言之

形如叉式结构的容易造成伪相关，A<-B->C，A<-B<-D->C这两个结构中A和C之间都存在混杂，结合D-分离方法，第一个结构可以通过以B为条件消除混杂，第二个结构可以以B或D为条件消除混杂。在消除混杂的时候我们需要关注的是对于哪两个变量来说，即从第二个结构来说，如果我们以B为条件可以得到A和B<-D->C，A和C之间的伪相关是可以消除的，但是B和C之间貌似还存在着伪相关。因此伪相关的消除，我们需要关注是去消除哪两个变量之间的伪相关。