搜索推荐中经常遇到的问题就是如何发现用户对某个商品的喜欢程度，也就是偏好，那么这个和矩阵分解又有什么关系呢？本文将尽量详细的解释这一点。

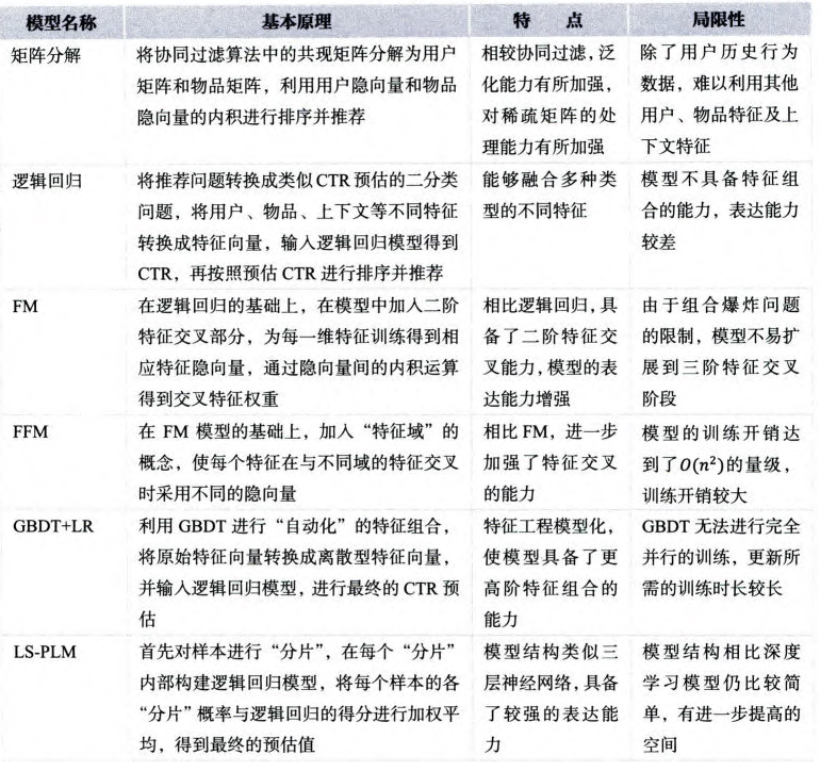
矩阵分解在推荐场景中的使用

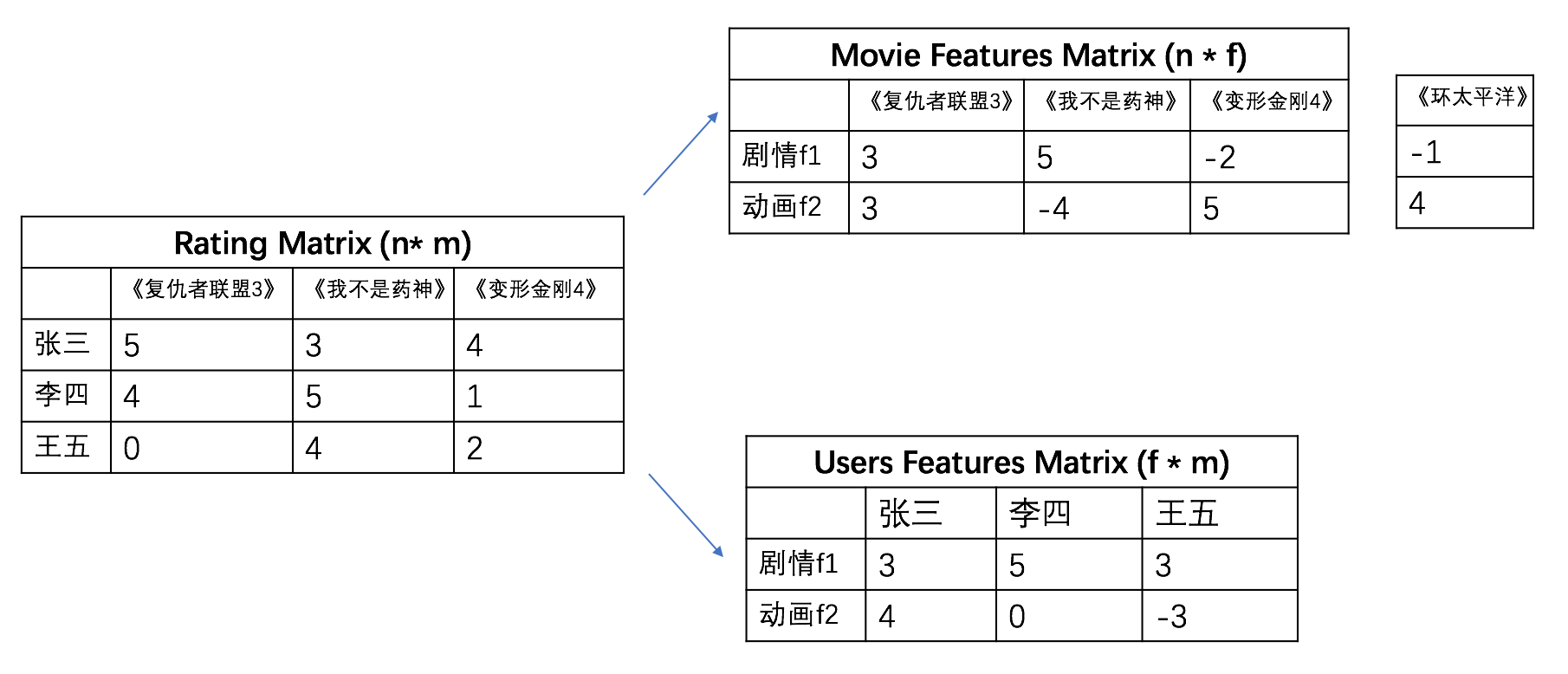
我们首先来看上面这个图片，左边的矩阵表示的一些用户对于一些影视作品的打分，俗称打分矩阵。右边两个矩阵分别表示将电影分成了剧情和动画，也就是中间的隐变量。
右边的两个矩阵是被分解的两个矩阵，怎么来使用这样的矩阵分解的结果呢？
如果想给李四推荐一个电影，应该怎么使用上面的矩阵呢？分别使用右上角的第二列，点乘右下角的第二列。 同理可以用右上角的第三列乘以右下的第二列

$$5*5+4*0=25 \\ -2*5+0*5=-10$$

可以看出李四应该是更喜欢我不是药神这样的剧情片。看起来还是十分好用的，那么目前的核心问题就是，右边这两个矩阵应该怎么获得呢？大学的时候一定学过SVD矩阵分解。它的一般形式是这样的。

$$A=V Σ U$$

然后通过选取Σ中前k大的奇异值，就可以对原先较大的矩阵A进行压缩。当我们要预测用户对电影的评分时，便可以直接从矩阵A中相对应的元素得到。
这种简单的思路，在实际运用中往往存在两个致命缺陷：

(1) 奇异值分解要求矩阵A是稠密的，也就是说不允许存在缺失值。而现实世界的User-Item矩阵却是存在大量空白的。
(2) 对M*N的矩阵进行奇异值分解的时间复杂度大约为$O(N^{3})$，这种计算量在大规模推荐场景下是无法接受的。

必须对这种SVD方法进行改进才能运用到真实推荐场景中。回顾下上述的奇异值分解方法，本质上是在平方损失下对矩阵的最优近似：

$$min |A-\bar{A}| \\ \bar{A}_{M \times N}= U_{M \times K} Σ_{K \times K} V^{T}_{K \times N}$$

FunkSVD

FunkSVD这种方法将以上的问题变成一个机器学习的问题，而不是纯粹意义上的矩阵分解问题。Funk的思想很简单，将评分矩阵A只分解为两个K维矩阵P和Q（相当于把奇异值矩阵融入了P或Q中），同时忽略A中的缺失值，这样最小化平方损失可以表示为：

$$L(P,Q) = min |A-\bar{A}| \\ \bar{A}_{M \times N}= Q_{M \times K} P^{T}_{K \times N} \\ min\ \frac{1}{2}\sum_{i=1}^{M}\sum_{j=1}^{N} I_{ij}(a_{ij}-\sum_{i=1}^{K}p_{ik}q_{jk})^{2}$$

其中$I_{ij}$当$a_{ij}$有评分就是1，否则就是0.
这就是FunkSVD最核心的损失函数.接下来来看下针对这样的参数如何进行梯度更新。

$$\frac{\partial L}{\partial P_{i}}=\frac{1}{2} \sum_{j=1}^{N} I_{ij} (a_{ij}-P_{i}Q_{j}^{T})^{2} Q_{j}\\ \frac{\partial L}{\partial Q_{j}}=\frac{1}{2} \sum_{j=1}^{N} I_{ij} (a_{ij}-P_{i}Q_{j}^{T})^{2} P_{i} \\$$

这种方法相当于把用户、物品映射到了K维空间中，最终的评分矩阵就有K个隐因子决定：

$$P=(p_{1},...,p_{k}) \\ Q=(q_{1},...,q_{k})$$

这样对于未出现过的评分，我们也可以通过相应的用户和物品的隐向量计算得到，极大地提高了模型的泛化能力。

到这里我们就构建好了P矩阵和Q矩阵，也就是上图中分解后的两个矩阵，使用这两个矩阵就知道每个用户喜欢每个电影的评分。这就是比较初期的推荐系统的原理。其实市面上目前很少使用矩阵分解的方式进行推荐搜索，因为矩阵分解依赖于我的用于都是有过一些记录的人，所以存在比较大的冷启动问题，所以目前大家更愿意把他当成一个点击率预估的任务，也就是一个经典的机器学习问题，也更容易被落地。但是并不是说咱们讲的没有任何用途，应该了解这些方式的优缺点和使用场景。才能以不变应万变。

接下来的章节中，咱们会讲解更多关于矩阵分解一些方法。

续表