基于值的深度强化学习算法
平均值DQN
平均值DQN是基于传统的DQN的一个简单但是非常有效的一个改进，它基于对先前学习过程中的Q值估计进行平均，通过减少目标价值函数中的近似误差方差，使得训练过程更加稳定，并提高性能。至于网络结构上是完全一致的。
算法分析
平均值DQN主要关注传统DQN学习过程中存在的误差，并想办法减少这些误差。
$Q(s,a;\theta_{i})$表示第i次迭代的值函数，
$$\begin{gathered}\Delta_{i}=Q(s,a;\theta_{i})-Q^{*}(s,a) \\
=Q(s,a;\theta_{i})-y^{i}_{s,a}+y^{i}_{s,a}-\hat{y}^{i}_{s,a}+\hat{y}^{i}_{s,a}-Q^{*}(s,a)\end{gathered}$$
其中$y^{i}_{s,a}$表示估计值，$\hat{y}^{i}_{s,a}$表示真实值。
$Z_{s,a}^{i}=Q(s,a;\theta_{i})-y^{i}_{s,a}$表示目标近似误差
$R_{s,a}^{i}=y^{i}_{s,a}-\hat{y}^{i}_{s,a}$表示过估计误差
$\hat{y}^{i}_{s,a}-Q^{*}(s,a)$最优差值。
$$\begin{gathered}y^{i}_{s,a}=E[r+\gamma max_{a'}Q(s',a';\theta_{t-1})|s,a] \\
\hat{y}^{i}_{s,a}=E[[r+\gamma max_{a'}(y^{i-1}_{s',a'}|s,a)]\\\end{gathered}$$
由于传统的DQN总是选取目标价值最大的动作执行，因此容易导致过估计。$Z_{s,a}^{i}$是在最小化DQN损失以后Q值和估计值$y_{s,a}^{i}$的一个误差。$Z_{s,a}^{i}$可能有多个原因造成。
- 由于不精确的最小化导致的参数$\theta$不准
- 由于经验池复用的大小限制泛化误差
而这个误差有是影响比较大的问题。每次迭代都依赖这个值的预测准确性。我们假设$Z_{s,a}^{i}$是一个随机过程，$E[Z_{s,a}^{i}]=0, Var=Z_{s,a}^{i}=\sigma^{2}$。 那么对于均值DQN就能过得到
$$
Q_{i}=Z_{i}+\gamma P \frac{1}{K} \sum_{k=1}^{K}Q_{i-k}
$$
P表示转移矩阵，$S \times S$, K表示最近K步的平均，进一步将模型转化为M状态的单项MDP。
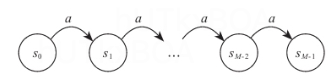
那么下面方差的变化就是
$$
VAR[Q_{i}^{A}(s_{0},a)]=\sum_{m=0}^{M-1} D_{k,m}\gamma^{2m}\sigma_{s_{m}}^{2}
$$
其中
$D_{k,m}=\frac{1}{N} \sum_{n=1}^{n}|U_{n}/K|^{2(m+1)}$，并且$U=(U_{n})_{n=0}^{n-1}$表示矩形脉冲是离散傅里叶变换，,$|U_{n}/K|<=1，D_{k,m}<\frac{1}{K}$.
因此意味着平均值DQN理论上能够有效的减少近似误差并且至少比普通的DQN好K倍。
伪代码
试用场景
传统的DQN在学习过程中可能出现学习过程中不稳定的问题，而平均值DQN通过计算之前学习的估计值的平均值生成了当前的动作价值估计，很好的解决了学习过程不稳定的问题，并且调高了DQN的学习性能。其实简单思考平均值DQN实际上是对值函数的一个平滑，进而减少估计误差。
基于动作排除的DQN
当我们面对动作空间很大情况下，这个时候我们经常使用逆向思维，通过一个模型学习最不可能的下一步动作，从而在最可能得动作中选择最好的值函数方法，这样既能加快学习的速度，还可以提升学习的质量。这个算法就是AE-DQN算法，本文就不过多介绍，感兴趣的可以通过论文阅读。
AE-DQN