什么是表示学习呢？说白了就是特征，机器学习算法的性能严重依赖特征。如果存在一种可以从数据中的到和判别特征的方法们就会减少机器学习对特征工程的依赖，这就是表示学习。

离散表示

这里虽然咱们单独拿出来讨论，但是其实特征的离散表示十分简单，就是独热编码，但是独热编码的缺点也是十分明显的。在向量空间中，所有的对象都是相互正交的，那么他们两两之间的相似度就是0，也就是这些对象之间没有任何关系，但是实际的生活中往往不是这个样子的，就不是粉色和浅粉色，他们都属于粉色，但是他们的相似度却是0，是不是有一点奇怪，所以独热编码一个比较本质的缺点就是会丢失大量的语义信息。

端到端学习是一种表示学习方法

基于重构损失的方法 – 自编码器

自编码器是基于深度学习模型的表示学习的典型方法，它的思路十分简单，就是输入映射到某个特征空间，再从这个特征空间映射回输入空间进行重构。从结构上看，它由编码器和解码器组成。

正则自编码器

如果我们放宽对于编码器维度上的限制，允许编码器的维度大于或者等于输入的维度，这种编码器称为过于完备的编码器。如果对于过于完备的自编码器不加任何限制，那么有可能不会学习到数据的任何有用信息，而仅仅是将输入复制到输出，导致这个问题的本质原因不是维度约束的变化，而是我们赋予编码器和解码器过去强大的能力，自编码器会倾向于直接将输入拷贝输出，而不会从数据中学到任何特征，因此我们对模型进行一些正则化约束。下面就是几种正则化约束。

去噪音自编码器

不同于原始的自编码器。去噪音自编码器的改进是将原始数据的输入的基础上加入一些噪音作为编码器的输入，解码器需要重构出不加噪音的原始输入x.通过这个约束,迫使编码器简单学习一个变幻，而必须从加了噪音的数据学习到有用的知识。

具体的做法就是随机将输入的x一部分设置成0，这样就得到了加噪音的输入作为编码器的输入解码器需要重构不带噪音的x。

$$L=\frac{1}{N}||x-g(f(x_{\theta}))||$$

稀疏自编码器

除了给输入加噪音，还可以通过损失函数上加入正则项使用模型学习到有用的特征。假设隐藏层使用sigmod函数，我们认为神经元的输出接近于1，它就是比较活跃的，相反的接近于0就是比较不活跃的。稀疏编码器就是以限制神经元活跃度约束吗，模型的，尽可能的使大大多数神经元处于不活跃的状态。
我们定义一个神经元的活跃度为它在所有样本上取值的平均，用$\vec{p_i}$表示，我们限制$\vec{p_i}=p_i$, $p_i$是一个超参数，表示期望的活跃度，通常是一个接近于0的值，通过对$p_i$偏离较大的神经元进行惩罚，就可以得到一个稀疏的编码特征这里我们使用熵作为正则项。

$$L_{sparse}=\sum p log \frac{p}{\vec{p_i}}+(1-p)log \frac{1-p}{1-\vec{p_i}}$$

相对熵可以量化表示两个概率的分布差异。加上稀疏惩罚以后，损失函数变成

$$L=L(x_i,g(f(x_i))) + \lambda L_{sparse}$$

变分自编码器

变分自编码器可以用于生成新的数据样本，它与传统的自编码器有很大的不同。
变分自编码器本质一个生成模型，它假设我们得到的样本都服从某个复杂的分布P(x)，生成模型的目的是建模P(x)，这样我们就可以从分布中进行采样，得到新的样本。
一般来说，每个样本都可能受到一些因素影响，比如手写数字，需要决定数字的大小，笔画的粗细，这些因素都是隐变量。假设这么多隐变量都用向量z表示，概率密度函数就是P(z),同时，有这样的一个函数$f(z;\theta)$，它可以把P(z)中采样的数据z映射与X相似的样本数据，就是P(X|z)的概率更高，引入隐变量后就求解P(X)的分布

$$P(X)= \int p(x|z)p(z) dz$$

对于隐变量z的选择，变分自编码器假设z的每个维度都没有明确的含义，而仅仅要求z方便采样，假设z服从标准正态分布 $z \sim N(0,1)$。而p(x|z)的选择常常也是正态分布，它的均值为$f(z;\theta)$，方差为$\delta^2 I$，其中$\delta$是一个超参数。

$$P(x|z)=N(f(z; \theta),\delta^2 I)$$

为什么上面的假设是合理的呢？实际上任意一个d维的复杂分布都可以通过对d维正态分布使用一个复杂点的变换得到，因此，给定一个表达能力足够强的函数，可以将服从正态分布的隐变量z映射为模型需要的隐变量。再将隐变量映射为x.

但是对于大部分的z，都不能生成与x类似的样本，就是p(x|z)通常接近于0，这对于估计p(X)没有任何意义，我们需要得到能够大概率生成比较像的x的z，这样的z怎么得到呢？如果知道z的后验分布p(z|x)，就可以通过x推断。变分自编码器引入了一个另一个分布q(z|x)来近似后验分布p(z|x)。现在的问题是$E_{z \sim q(z|x)}[p(x|z)]$与p(x)的关系是怎么样的？下面我们来计算q(z|x)和p(z|x)的KL距离。

$$D_{KL}[q(z|x)||p(z|x)]=E_{z \sim q(z|x)}[log q(z|x)-log p(z|x)]$$

然后使用贝叶斯公式

$$D_{KL}[q(z|x)||p(z|x)]=E_{z \sim q(z|x)}[log q(z|x)-log p(x|z)-log p(z)]+log p(x)$$

$$log p(x)- D_{KL}[q(z|x)||p(z|x)]=E_{z \sim q(z|x)} [log (p(x|z))]-D_{KL}[q(z|x)||p(z)] \tag{1.1}$$

公式1.1就是整个变分自编码器的核心，左边包含我们要优化的目标p(x),当我们选择q(z|x)表达能力足够强的时候，可以近似表达p(z|x)，也就是说，$D_{KL}[q(z|x)||p(z|x)$是一个趋近于0的数字。右边第一项实际上就是一个解码器,将基本的输入x得到最有可能的相似样本的隐变量采样出来，通过解码器生成样本，右边第二项是一个正则项。那么我们进一步分析，前面假设p(x|z)是正态分布，对于下面的公式右边第一项，计算得到损失函数的第一部分重构损失，注意这里取负号是由于梯度下降进行优化，因此目标变为最小化-p(x)。$f(z;\theta)$使用神经网络来实现。

$$-log p(x|z)=-log \frac{1}{\amalg \sqrt{2π \delta^2}}exp(-\frac{(x-f(z;\theta))^2}{2 \delta^2}) = \frac{1}{\delta^2} (x-f(z;\theta))^2 +constant$$

对于q(z|x)的选择，我们假设服从正态分布，它的分量相互独立

$$q(z|x)=log \frac{1}{\amalg \sqrt{2π \delta_{i}^{2}(x)}}exp(-\frac{(z-\delta(x)^2)}{2 \delta(x)})$$

$$D_{KL}[q(z|x)||p(z)]=\frac{1}{2} \sum_{i=1}^{d}(\mu){i}^{2}(x)+\delta_{i}^{2}(x)-ln \delta_{i}^{2}(x) -1 )$$

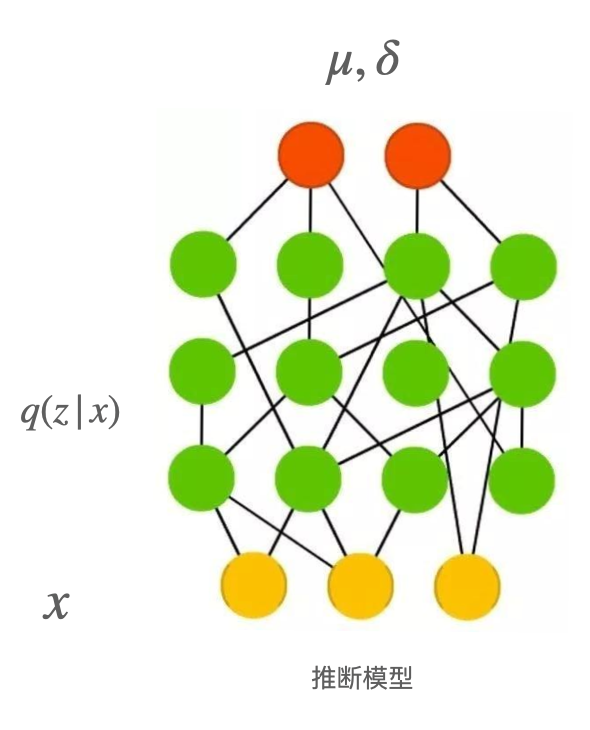
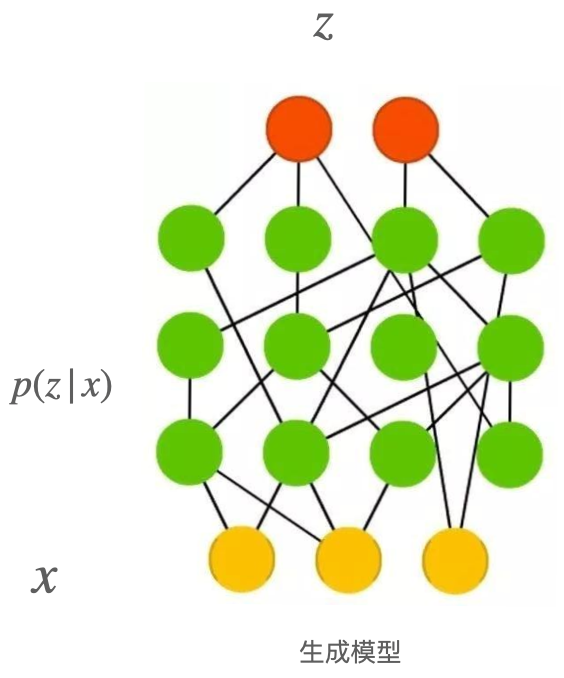
最后一个问题就是隐变量z通过采样得到，而采样这个操作是不可导的，无法进行反向传播，我们使用一个称为重参数化的技巧来解决这个问题，具体说就是先从正态分布N(0,1)中采样得到$\sigma$，隐变量z通过计算得到$z=\sigma \mu(x)+\delta(x)$，这样就解决了反向传播的问题。

再看word2vec

我们之前讲过word2vec，可能当时比较笼统，现在我们学习了自编码器以后，我们再看看word2vec到底是怎么回事。

词向量模型

word2vec其核心思想是用一个词的上下文去刻画这个词。从这个思想出发，我们有两种不同的模型。一种是给定某个中心词的上下文去预测当前词，这个模型就是咱们说过的CBow,另一个是给定一个中心词预测它的上下文。这个模型叫做skip-gram。

下面我们来具体看看这个模型是怎么运作的。给定一个语料库，可以是多篇文档构成，假设语料库可以表示为一个序列 $C=(w_1,w_2...w_n)$。语料库长度为N，单词的词表为V，$w_i \in V$。skip-gram模型是使用中心词预测上下文，这样定义上下文词为中心的某个窗口词。给定中心词，要能够准确的预测上下文词。

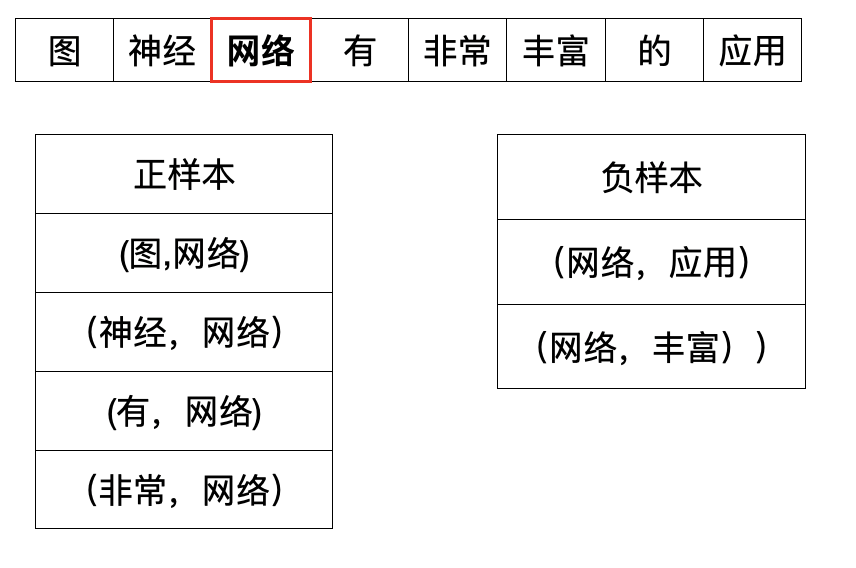
假设中心词是“网络”，那么构建的正负样本是怎么样的？
如上图所展示的一样，离中心词指定范围内的词就是负样本。
我们的目标是找到使得条件概率$p(y=1|(w_c,w))$和$p(y=0|(w_c,w))$最大化的参数$\theta$

这个问题就转化为一个二分类问题啦，给定任意两个词，判断他们是否是上下文词。可以使用逻辑回归来建模这个模型，引入两个矩阵$U \in R^{D \times d} $, $V \in R^{D \times d}$，他们中的每一行都代表一个词语，在模型训练完以后，U、V分别对应作为中心词和上下文词两种角色的不同表达。对应的一个词w，定义$U_{w}$表示他的词向量。$p(y|(w_{c},w))$表达如下形式

\begin{cases} \begin{align} \delta(U_{w_{c}} \bullet V_{w}) \\ 1- \delta(U_{w_{c}} \bullet V_{w}) \\ \end{align} \end{cases}

其中$\delta$是sigmod函数。联合上面两个公式取对数，可以得到如下公式，也就是skip-gram的目标函数

$$L=-\sum log \delta(U_{w_c} V_w)-\sum log \delta(1-U_{w_c} V_w)$$

$U_{w_c}$ 是中心词的词向量表示
$V_w$ 是正确的上下文词的词向量表示

上面这个公式一方面增大了正样本概率，另一方面减少负样本的概率。所谓的增大正样本的概率实际上就是增加$U_{w_c} \bullet V_w$,也就是中心词与上下文的内积，也就是他们之间的相似度。反之亦然。

这种构建正负样本，并最大化正样本之间的相似度，最小化负样本之间的相似度方式是表示学习中构建损失函数的一种常用思路。这类损失我们称为对比损失。
这里需要表达一下，一个词在不同句子中，他的词向量有可能是不一致的。