贝叶斯网络(四)--完整数据集下的参数学习

本节主要讲完整数据集下的参数学习，在贝叶斯网络中参数就是计算路径概率的时候，每条连边的概率。对于这个概率主要有两种做法，这一种是频率学派，一种贝叶斯学派。

频率学派

这种方法是最容易理解和做的，直接调过证明过程，看一个小例子。看如图1的概率关系。

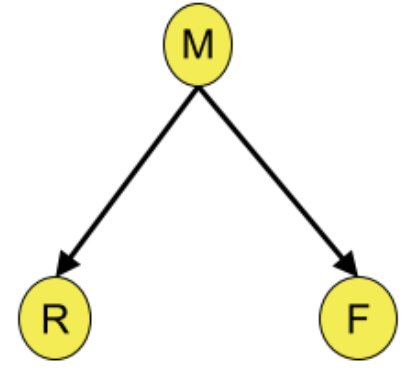
M	F	R
$m_{0}$	bad	O
$m_{0}$	bad	O
$m_{0}$	bad	O
$m_{0}$	bad	O
$m_{0}$	bad	N
$m_{0}$	good	O
$m_{1}$	bad	O
$m_{1}$	bad	N
$m_{1}$	good	O
$m_{1}$	good	N
$m_{1}$	good	O
$m_{1}$	good	N
$m_{1}$	good	O
$m_{1}$	good	N
$m_{2}$	good	N

P(M=m_{0})=\frac{6}{15} \\ P(M=m_{1})=\frac{8}{15} \\ P(M=m_{2})=\frac{1}{15} \\

P(F=good|M=m_{0})=\frac{1}{6} \\ P(F=bad|M=m_{0})=\frac{5}{6} \\

这样就简单的将参数构建好了，基于一个完整的数据。

基于最大后验分布的参数估计

基于最大后验分布的参数估计假设先验分布是Dirichlet分布，那么参数 $\theta_{ij}$ 的后验分布为

P(\theta_{ij}|D)=Dir(\theta_{ij}|a_{ij1}'+a_{ij1},...,a_{ijr}'+a_{ijr})

利用求数学期望对参数进行估计

\theta=\frac{a_{ijk}'+a_{ijk}}{\sum_{k=1}^{r} a_{ijk}'+a_{ijk}}

这里可以举出一个例子，对于射击手来讲，一个队员射击了10次，中靶6次，和另一个队员设计100次，中靶60次，命中率都是60%。结论是水平相当。假设先验信息没有数据的情况，那么使用均匀分布作为其分布，咱们假设 $a_{ijk}=1$ , 那么第一个队员的实际命中率就变成了 $\frac{1+6}{2+10}$ ,第二个队员的水平是 $\frac{1+60}{2+100}$ ，明显第二个队员的水平更加靠谱一点。