基于样本的迁移学习
本节讲解基于样本的迁移学习，这个时候你可能会有疑问，基于样本如何迁移呢？难到是直接把源数据直接做学习吗？ 当然这种方法已经被证明效果方差较大，很难真正使用。其实基于样本的迁移学习主要要解决两个问题。
- 如何筛选源域中的目标数据具有”相似分布”的有标签数据
- 如何利用这个“相似”的数据进行学习
通过上节的学习我们知道一个域分为两部分$D=\{X, P^{x}\}$, 其中X是特征空间，$P^{x}$表示边缘分布，给定D，一个任务T表示为$\{Y, P^{Y|X}\}$,标签空间Y，条件概率分布$P^{Y|X}$，这里还能进一步进行分类。当$P_{s}^{X} \neq P_{t}^{X}，P_{s}^{Y|X} = P_{t}^{Y|X}$.称为非归纳迁移学习，如果$P_{s}^{Y|X} \neq P_{t}^{Y|X}$则称为归纳迁移学习。 例如一个意愿利用病例训练出一种特殊疾病的预测模型，在这里每家医院都是一个域，由于不同医院的病人分布不同，不同于的边缘概率$P^{X}$不同。然而由于各家医院研究的都是同种疾病，所以条件概率是相同的$P^{Y|X}$,这就是非归纳迁移学习的一个典型应用场景。如果将前面的例子这种疾病是新冠病毒，新冠病毒可以演变出各种各样的变体所以$P^{Y|X}$不同，这就称为了归纳迁移学习。
基于样本的非归纳迁移学习
上文也讲到了，基于样本的非归纳迁移学习主要的特点是源域和目标域的不同之处在于输入样本的边缘分布，在这样的假设下，源域是有标签的数据，而目标域是无标签数据。接下来来看一下如何做到这样的迁移学习。
对于一般的机器学习算法，是希望训练处一个参数集合$\theta_{t}$来预测模型，优化如下的经验风险最小化。
$$
\theta_{t}=arg\ min E_{x,y \in P_{t}^{X,Y}}L(x,y,\theta) \tag{1.1}
$$
$L(x,y,\theta)$表示损失函数,很明显，目标域是没有标注数据，所以无法通过训练获得模型参数。通过贝叶斯定理和期望的定义可以转化为如下的问题。
$$
\theta_{t}^{*}=arg\ min E_{x,y \in P_{t}^{X,Y}}[\frac{P_{t}(x,y)}{P_{s}(x,y)}L(x,y,\theta)] \tag{1.2}
$$
根据非归纳迁移学习的定义，由于$P_{s}^{Y|X} = P_{t}^{Y|X}$,通过联合概率分布$P^{X,Y}=P^{Y|X}P^{X}$,可以得到$\frac{P_{t}(x,y)}{P_{s}(x,y)}=\frac{P_{t}(x)}{P_{s}(x)}$,上图1.2的公式如下。
$$
\theta_{t}^{*}=arg\ min E_{x,y \in P_{t}^{X,Y}}[\frac{P_{t}(x)}{P_{s}(x)}L(x,y,\theta)] \tag{1.3}
$$
源域样本x的权重为目标域和源域在数据点x处的样本的边缘分布比。给定源域的样本分布，给定$\beta(x)=\frac{P_{t}(x)}{P_{x}(x)}$,公式1.3可以改写成如下形式。
$$
\theta_{t}^{*}=\sum_{i=1}^{n} \beta(x_{s_{i}})L(x_{s_{i}}, y_{s_{i}},\theta_{t}) \tag{1.4}
$$
通过上面的公式可以看出，如果想要使用源域的数据估计目标域的数据，就要知道权重比即$\beta(x_{s_{i}})$,一个简单的估计方法是估计$P_{t}^{X}$和$P_{s}^{X}$，然后对每个样本计算密度比，然而这也是一个很难的任务。下面咱们就介绍一个估计密度比的方法。
区分目标数据和源数据
学习权重是一个比较简单的方法是把估计密度比的问题转化为判别一个样本属于源域还是目标域的问题，也就是一个经典的二分类问题，接下来咱们来介绍一个“拒绝采样”的策略估计密度比。
引入一个选择变量$\delta \in [0,1]$,以$P_{t}(X)$的概率从边缘分布$P_{t}^{X}$从抽取目标样本x，其中$P_{t}(x)=P(x|\delta=0)$,x以$P(\delta=1|x)$的概率被源域接受以$P(\delta=0|x)$被拒绝，每个数据x处的密度比为
$$
\frac{P_{t}(x)}{P_{s}(x)}=\frac{P(\delta=1)}{P(\delta=0)} \frac{P(\delta=0)}{P(\delta=1)}\frac{P_{t}(x)}{P_{s}(x)} \tag{1.5}
$$
其中$P(\delta)$是$\delta$在目标域和源域的联合数据集内的先验概率,以上公式进一步改成
$$
\frac{P_{t}(x)}{P_{s}(x)}=\frac{P(\delta=1)}{P(\delta=0)} (\frac{1}{P(\delta=1|x)}-1) \tag{1.6}
$$
我们把$P(\delta=1|x)$看成是一个二分类的训练器。计算完成每个源域样本的密度比，对源数据进行重加权训练就可以得到一个新的目标域模型。
函数估计
函数估计是将密度比视为一个未知函数，通过学习一组基函数组合来估计它，被称为协变量移位法，通过定义$\frac{P_{t}(s)}{P_{s}(x)}$为函数w(x).
$$
\bar{w(x)}==\sum \alpha f(x)
$$
其中$\alpha$是要学习的参数，f是基函数，$P_{t}(x)$可以通过$P_{t}(x)=\bar{w(x)}P_{s}(x)$,这样就解决了迁移学习的目的。
基于样本的归纳迁移学习
之前讲过，在基于归纳迁移学习的任务中，源任务和目标任务的条件概率分布式是不同的，因为目标任务没有训练数据，也很难通过源任务直接进行训练因此在归纳迁移学习中，除了源域存在标注数据，目标任务也会有少量的标注数据。目标是让目标任务能够提升预测精度。
样本生成
其中一种方法是通过样本生成的方式为目标任务构建更多的可用数据，其中一种方法是通过深度生成模型改变图片的风格来创建新的样本，就是保持目标图片内容不变只是修改风格。然后训练模型的时候会设置两个损失函数一个是风格损失一个是内容损失，通过这样的方式提高训练的精度。这类方法局限性比较大，后续我们也会介绍更多的样本生成方法。
boosting风格方法
基于boosting的方法是通过更新源域样本找到那些误导的源数据，典型的方法有TRAdaBoost,TRAdaBoost在源域和目标域中的联合数据集合中训练一个模型H，利用H对目标域数据进行预测，并计算目标域的平均损失，即 $\sigma=\frac{\sum w_{i}L(H(x),y)}{\sum w_{i}}$,w是x对应的权重，L是损失函数，对于每一个目标样本，其权重更新为$w_{i}^{t}=w_{i}^{t} \beta^{-L(h(x),y)}$, 其中$\beta=\frac{\sigma}{1-\sigma}$,如果某个目标域数据有较高的损失，权重将会在下一轮迭代中修改权重，这和原生的boosting算法一致。而对于源域的数据，如果损失过高就不利于目标任务，权重将会被降低，通过这样的一个方式就能够减少源域的数据对目标域数据的影响。并且为目标学习一个分类器。
总而言之
希望大家的工作学习中能够遇到类似的问题，并将自己的问题抽象成一个迁移学习问题。
基于特征的迁移学习
接下来我们来讲解基于特征的迁移学习，本章主要介绍基于同构的迁移学习，也就是满足假设，$X_{s} ∩ X_{t},Y_{t}=Y_{s}$,一个普遍的想法是学习一对映射函数，$[\psi_{s}, \psi_{t}]$,能够将源域的特征和目标域的特征映射到共同的特征空间。使得域之间的差异性减少，使用映射之后的源域和目标域的新特征空间进行训练，从而提升学习效果。
最大均值差异
最大均值差异是一种非参数度量，给定两个域的特征$X_{s}, X_{t}$,其MMD距离经验估计为
$$
MMD(X_{s}, X_{t})=\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \phi(x_{i}^{s})-\frac{1}{n_{t}} \sum_{i=1}^{n_{t}}\phi(x_{i}^{t}) \tag{1.1}
$$
其中$\phi(x)$表示每个实例映射到与核$k(x_{i},x_{j})=\phi(x_{i})^{T}\phi(x_{j})$相关联的空间。通过使用核函数，可以将公式1.1简化
$$
MMD(X_{s}, X_{t})=tr(KL) \tag{1.2}
$$
其中tr表示矩阵的迹，
$$
\begin{equation}
K=
\left(
\begin{array}{ccc}
K_{s,s} & K_{s,t} \\
K_{s,t}^{T} & K_{t,t} \\
\end{array}
\right)
\end{equation}
$$
由源域、目标域和交叉域组成，L是一个矩阵。
$$
L_{ij}=
\begin{cases}
\begin{align}
\frac{1}{n_{s}^{2}}\ x_{i},x){j} \in X_{s} \\
\frac{1}{n^{2}}\ x_{i},x_{j} \in X_{t} \\
\frac{1}{n_{t}*n_{s}}\ x_{i},x_{j} \in X_{s} \\
\end{align}
\end{cases}
$$
以上就是基于特征迁移学习的一般思路，下面介绍常用的方法。
最大均值差异嵌入（MMDE）
MMDE是一种用于迁移学习的降维算法，其主要思想如下
$$\begin{gather}min\ MMD(\phi(X_{s}, X_{t})) + \lambda \Omega(\phi) \\
s.t. \phi(X_{s}, X_{t})约束 \tag{2.1}\end{gather}$$
其中$\phi$是需要学习的，将原始数据映射到一个低纬度的空间的交叉域中，目标的描述是最小化源域数据与目标数据的MMD距离，而$\Omega(\phi)$是映射函数的正则项，约束条件的意思是保留原有数据的特性。
从上面的描述也能看出来，其实所谓的迁移只是我们将源数据和目标数据进行一部分的映射，对于映射过来的数据进行一个学习，从而达到迁移学习的作用。
基于深度学习的迁移学习
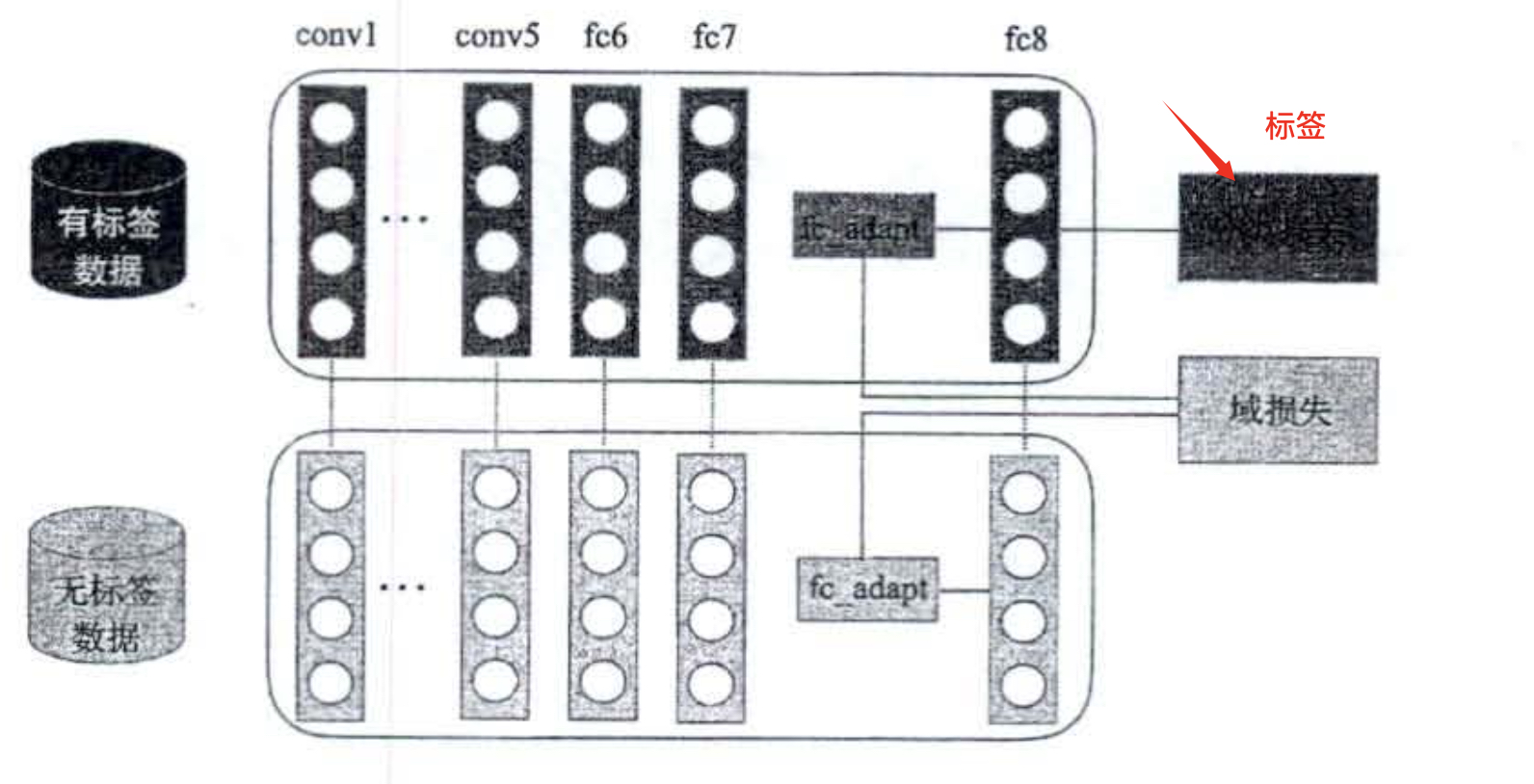
深度学习的架构一般如上图，前几层的特征转换其实相当于是MMDE中的$\phi$的一种近似，关键是想区分源数据中和目标数据中的域损失，从而最大化域损失。
基于Bregman的散度的正则化
除了使用MMD这种衡量方式，还有一种基于Bregman距离的迁移空间方法，目标函数如下。
$$
min\ F(\phi) + \lambda D_{w}(\phi(X_{s}|\phi(X_{t}))
$$
其中$F(\phi)$是任务特定的目标函数，例如分类误差，而$D_{w}(\phi(X_{s}|\phi(X_{t}))$表示$\phi(X_{s})$和$\phi(X_{t})$的Bregman散度。
基于模型的迁移学习
本节其实在元学习系列已经进行一个大部分的讲解，所谓的基于模型的迁移是说如果在已有的模型中抽取出对当前学习有效的知识，而这里所谓的知识就是权重。下面就轻量级的讲点之前没有提到的东西
基于贝叶斯的迁移学习
基于贝叶斯的迁移学习目前应用在一些自然语言处理的任务中。使用在文本分类任务，一般如下两个步骤。
- 以概率分布的形式对先验的知识进行迁移。利用朴素贝叶斯在源域的数据中建立模型。
- 该算法使用EM算法求解目标域模型，使用KL散度度量两个域的差异。多轮推演减少新学习的模型与目标分布的差异。这其实就是一个相对学习的过程。
利用深度学习迁移
在深度学习中，往往使用知识蒸馏的方式进行知识迁移，知识蒸馏涉及到一个教师网络和一个学生网络，标签也是软标签，最初是为模型压缩提出的。在处理压缩的过程中，源域和目标域被认为是一致的。
基于深度的迁移学习中，通过计算类别k所有源样本的激励函数的平均值，可以提取类别k的软标签l。下图就是一个例子，其中向量的每个维度表示bottle和每个类别的相似性，通过学习发现bottle的软标签和杯子的权重比键盘的更高。通过训练这样的软标签，可以刻画bottle，杯子，键盘的特征空间的关系
知识蒸馏
知识蒸馏，可以将一个网络的知识转移到另一个网络，两个网络可以是同构或者异构。做法是先训练一个teacher网络，然后使用这个teacher网络的输出和数据的真实标签去训练student网络。知识蒸馏，可以用来将网络从大网络转化成一个小网络，并保留接近于大网络的性能；也可以将多个网络的学到的知识转移到一个网络中，使得单个网络的性能接近emsemble的结果。
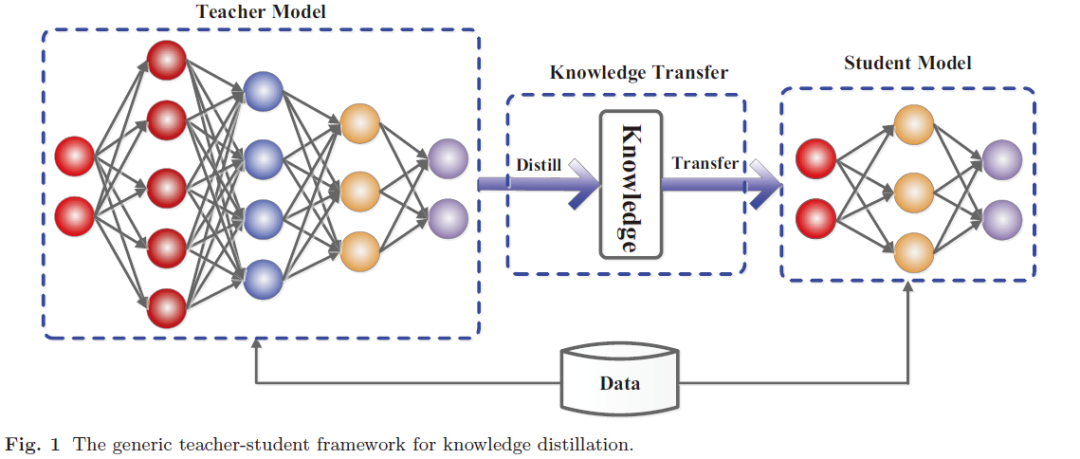
蒸馏模型的一般框架，在典型的图像分类任务中，logit（例如深层神经网络中最后一层的输出）被用作教师模型中知识的载体，而训练数据样本未明确提供该模型。例如，猫的图像被错误地归类为狗的可能性非常低，但是这种错误的可能性仍然比将猫误认为汽车的可能性高很多倍。另一个示例是，手写数字2的图像与数字3相比，与数字7更相似。这种由教师模型学习的知识也称为暗知识（“dark knowledge”）。一般会将logit替换成如下的形式。防止标签过硬，T是超参数。
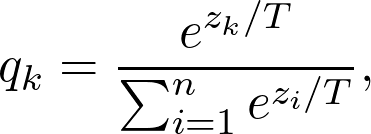
- 训练一个能够性能很好泛化也很好的大模型。这被称为教师模型。
- 利用你所拥有的所有数据，计算出教师模型的预测。带有这些预测的全部数据集被称为_知识_，预测本身通常被称为_soft targets_。这是知识蒸馏步骤。
- 利用先前获得的知识来训练较小的网络，称为学生模型。