今天我们来看看机器学习入门课程中的最小二乘法,是不是感觉咱们越学习越回退啦,其实学习的过程是这个样子,你知道的越多,你之前的认知发生改变的概率越大,可能之前是硬性的理解,现在是真正的理解,好啦,话不多说,咱们来看看从因果推断的角度如何看待最小二乘法这个算法。
回归模型使用如下的表达式
Y=X′β+ϵE(ϵ∣X)=0(1.1)
其中β是学习的系数,而X’是解释变量,ϵ是残差,这个回归模型对应的CEF(条件期望函数)是
E(Y∣X)=X′β+ϵ(1.2)
我们发现这个CEF可以是因果关系,也可以是相关关系。如上节讲到的,要看ϵ是否有影响解释变量的因素存在。
我们通过最小二乘法求解β^,就是最小化被解释变量值Y和解释变量X的线性预测值Y′=X′b的残差平方的期望值,也即是求解如下的方程
β^=argmin E(Y−X′b)2(1.3)
上式最小化的条件就是对b的一阶导数为0,这都快回到高中啦。也就是β^满足
E[X(Y−X′β^)]=0(1.4)
同等于
E(Xϵ)=0
由此可见,最小二乘法的本质是求解系数β^,使得解释变量X和残差ϵ不相关。等式1.4的解为
β^=E(XX′)−1E(XY)(1.5)
将回归模型1.1带入到1.5
β^=E(XX′)−1E(XY)=E(XX′)−1E(X(X′β+ϵ))=β+E(XX′)−1E(Xϵ)
其中E(XX′)−1E(Xϵ)是差异项,当E(Xϵ)=0的时候,就意味着β^=β.
通过上面的分析,我们是能够得到这样的结论。
- 如果对应条件的期望函数是因果关系的CEF,那么求出来的β就是因果关系的解释
- 如果对应条件的期望函数是相关关系的CEF,那么求出来的\hat{\beta}仅仅具有相关关系的解释
多元回归系数的直观理解
从上面的学习中,我们通过最小二乘法的求解过程,推导了一下它们之间的关系,本节我们通过最直观的方式理解最小二乘法,也就是说最小二乘法是如何解析多个影响因子的系数关系呢?这里我们还通过EDU和IQ对INC的影响这样的案例来学习。我们来分析以下三种情形
INC、EDU和IQ的变化都是相关的
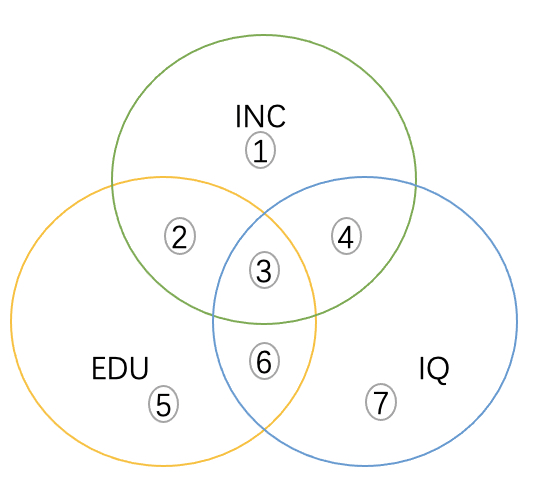
我们如果直接将INC和EDU进行回归,就是图中2和3的信息被用于估计EDU和INC的关系,这样得出的系数反应的是INC和EDU的相关性,也就是r1,1和4是INC变化和EDU无关的部分,也就是INC对EDU回归残差的变化。以此类推每两部分的关系都如上描述,但是将INC和EDU和IQ同时回归,情况就不太一样。EDU的影响是β1是有2造成的,IQ影响的β2是因为4造成的。这里的关键是,为什么舍去了3的信息呢?这样做的原因是。3是EDU、IQ公共变化的部分。这些变化对INC的影响是不确定的,所以就索性忽略掉。2和4反而是直接与INC相关的部分,使用2和4的信息估计对INC的影响也就是因果的关系。这里咱们进一步映射一下,咱们求偏导数的过程,是假设另一个变量为常数,对其中一个因变量求导,是不是和咱们讲的这个过程十分相似。
EDU和IQ重合面积大
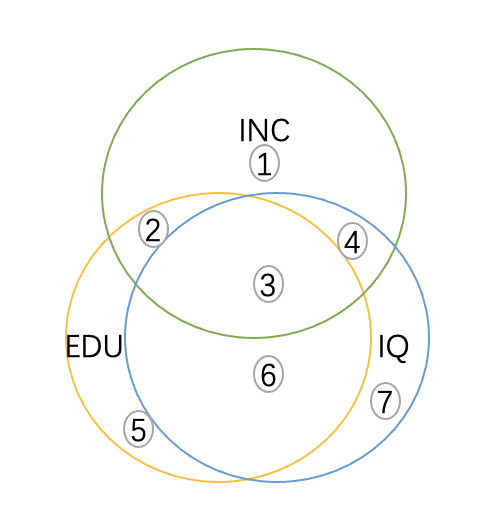
这里描述的情形就是EDU和IQ严重共线的情况,在这种情况下,能提供给我们分布估计EDU和IQ对INC的影响非常少,回归出来的结果β1和β2在统计上很难统计显著,在极端情况下,当EDU和IQ重合的时候,没有2和4求解系数,此时无法估计β1和β2。
INC和EDU和IQ均相交,但是EDU和IQ不相交
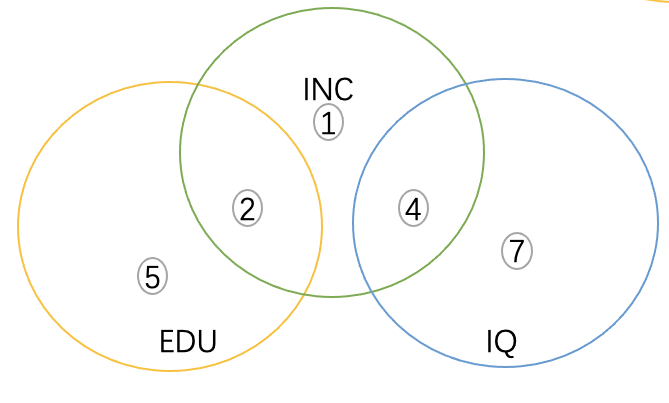
这种情况下,INC对EDU和IQ同时回归和单独回归最后的结果是一样的,因为两个解释变量是相互独立的。简而言之,当两个解释变量不相关的时候,缺失其中一个都不会影响回归系数,并且这样的情况,能很好的回归出系数,且不存在偏差。
总结
读完这一章节的内容,对大家的做特征有没有什么启发呢,不同特征之间的关系放到一起到底起到一个什么样的效果,模型又是如何学习这些知识的呢?你现在能想清楚吗?