因果推断(一)--线性回归

讲线性回归之前，我们先来接受因果推断的一些名词，充充场面。记得咱们上节讲的教育程度（EDU）对收入（INC）的因果影响吗？ 这里我们将EDU和INC称为可观测变量,EDU也称为处置变量，智商（IQ）是另一个可观测变量。由于EDU和IQ都会影响收入INC，它们同时被称为解释变量，INC称为被解释变量。要单独估计EDU和INC的因果影响要控制IQ对INC的影响。我们经常把无法观测的变量称为干扰项e，所以我们上面的描述能够用一个方程来表示。

$$INC=\alpha+\beta_{1}EDU+\beta_{2}IQ+e \tag{1.1}$$

我们希望能够识别出变量EDU和INC的因果影响$\beta_{1}$，由于干扰项无法观测，所以即使我们观测到INC和EDU和IQ的变化关系，并不能确定EDU对INC的影响有多大，因为它们之间变化的相关性可能是有e造成的。因为e中可能包含一些影响INC的特征，所以变量EDU和INC的正相关性可能是由于e中的某些特征引起的，而并非因为二者的因果关系影响，也就是说无法识别$\beta_{1}$,如下图a就是这个意思。

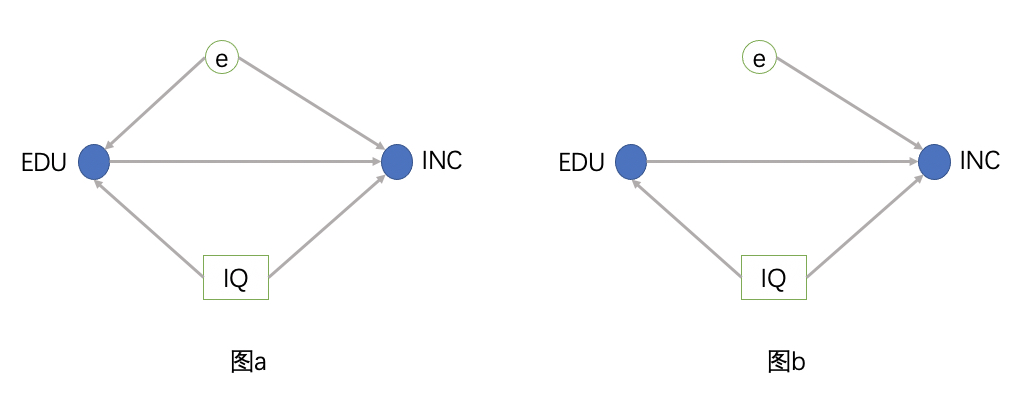
如果我们的因果关系如图b的样子，那么当我们控制了IQ以后，EDU到INC只有一条因果路径，此时我们就可以通过EDU和INC的相关关系确认二者的因果关系，当给定IQ的值，EDU的变化和e无关，那么EDU和INC的相关关系就直接反映啦因果关系识别$\beta_{1}$。

因果关系条件期望函数

如果想达到图b的样子，就是干扰项e和EDU在控制IQ后不存在混淆路径，也就是说干扰项条件均值独立于解释变量。

$$E(e|EUD,IQ)=E(e)=c \tag{1.2}$$

干扰项的平均值等于常数c，这个条件就意味着给定EDU和IQ的个体，他们的干扰项平均值是c，也就是说随着EUD和IQ的变化干扰项的平均值不会发生变化，这种情况下就能求出$\beta_{1}$和$\beta_{2}$。
我们可以举个例子，当IQ=iq的时候，当EDU从10增加到11的时候，干扰项均值不变，也就是$E(e|EUD=10,IQ=iq)=E(e|EUD=11,IQ=iq)=c$,INC均值变化为。

$$E(INC|EUD=11,IQ=iq)-E(INC|EUD=10,IQ=iq) \\ =[\alpha-11\beta_{1}+\beta_{2}iq+E(e|EUD=11,IQ=iq)] \\ - [\alpha-11\beta_{1}+\beta_{2}iq+E(e|EUD=10,IQ=iq)] \\ =\beta_{1}$$

在上面这种情况下，INC的变化完全归因于EDU的变化。
综上所述，能够识别出解释变量和被解释变量因果关系的线性规划模型要满足以下两个假设。

1. 线性关系假设，$INC=\alpha+\beta_{1}EDU+\beta_{2}IQ+e$
2. 干扰项条件均值为0假设，$E(e|EDU,IQ)=0$
   对于条件2，是我们在线性回归的常数项和常数c的一个合并。

由此可见，线性回归模型的两个假设对应的线性条件期望函数（CEF）

$$E(INC|EUD,IQ)=\alpha-\beta_{1}EDU+\beta_{2}IQ + 0$$

回忆一下我们在求线性回归的解的时候，使用什么样的方法呢？

$$\frac{dE(INC|EDU,IQ)}{dEDU}=\beta_{1} \\ \frac{dE(INC|EDU,IQ)}{dIQ}=\beta_{2} \tag{1.3}$$

在数学中，一个多变量函数求偏导数就是指保持其中一个变量不变，该函数关于其中一个变量的导数。所以是不是豁然开朗，原来我们求线性回归的时候其实已经有些一些因果推断的思想啦

相关关系条件期望函数

下面我们来看看加入干扰项不独立与解释变量，那么我们如何做因果分析，或者说还存在因果分析的可能吗？

$$INC=\alpha+\beta_{1}EDU+e’ \tag{1.4}$$

上面公式中的$e‘=\beta_{2}IQ+e$，也就是说我们在开始分析这个问题时候没有发现IQ这个解释变量，并且IQ和EUD具有相关性。

$$E(e'|EUD)=E(\beta_{2}IQ+e|EDU)=\beta_{2}E(IQ|EDU)\neq0$$

这种情况下，干扰项不满足条件均值为0的假设，此时描述模型如下

$$INC= \alpha+\beta_{1}EDU +e' \\ E(e'|EDU)\neq0$$

因为干扰项中包含IQ这个变量，当EDU变化的时候，干扰项也会变化，这就是让我们不能识别EDU和INC的单独因果影响，也就无法识别模型的系数$\beta_{1}$。这种情况下我们经常会得到一些错误的结论，例如说INC和EDU不相关之类的结论。在错误的理解下，我们经常会构建如下的模型。

$$INC= r_{0} + r_{1}EDU + u \\ E(u|EDU)=0$$

可以理解这里建模的$INC= r_{0}+r_{1}EDU + u$ 和 $INC= \alpha+\beta_{1}EDU+e'$的意义是不同的。我们可以进一步的理解$r_{1}$和$\beta_{1}$的关系。错误模型的CEF为：

$$E(INC|EDU)=r_{0}+r_{1}EDU$$

对EDU求导数可以得到

$$\frac{dE(INC|EDU)}{dEUD}=r_{1}$$

$r_{1}$反应的是INC的期望如何随着EDU变化，但是没有保持IQ不变，也就是没有截断混淆路径。这就与公式1.3中求$\beta_{1}$不同。$\beta_{1}$的含义是保持IQ不变，INC的期望如何随着EDU变化。这时候你可能好奇$\beta_{1}$和$r_{1}$是什么关系呢？
我们将$INC=\alpha+\beta_{1}EDU+\beta_{2}IQ+e$带入到$E(INC|EDU)$中

$$E(INC|EDU)=E(\alpha+\beta_{1}EDU+\beta_{2}IQ+e | EDU) \\ =\alpha+\beta_{1}EDU+\beta_{2}E(IQ|EDU) \tag{1.5}$$

对公式1.5求导。

$$\frac{dE(INC|EDU)}{dEDU}=\beta_{1}+\beta_{2}\frac{E(IQ|EDU)}{dEDU} = r_{1}$$

假设EDU和智商IQ存在线性关系。

$$E(IQ|EDU)=\sigma_{0}+\sigma_{1}EUD$$

就是受教育程度高的个人平均智商也高，那么

$$\frac{dE(IQ|EDU)}{dEDU}=\sigma_{1}$$

最终

$$r_{1}=\beta_{1}+\beta_{2}\sigma_{1}$$

经过这么一堆推导，可以看出$r_{1}$只是反应了EDU和INC的相关性，它包含受教育程度EDU对收入INC的因果影响$\beta_{1}$，以及受教育程度EDU和IQ的相关性$\sigma_{1}$乘以IQ对INC的因果影响$\beta_{2}$。可见这个结果作为因果关系使用是十分不靠谱的。