这个系列我们来介绍一下因果推断,这个时候第一反应应该是因果推断是什么呢?解决什么问题的呢?咱们举几个例子来说明下,例如你会不会经常有这样的疑问?读博士能增加收入吗?如果能增加增加多少呢?其实这其中就包含了因果推断的内容,表面你是抛出了一个疑问,其实你是想了解读博士和收入增加有没有因果关系,“别人家的孩子”的成就中,读取博士到底与他们的生活有多大关系。是不是因为读取了博士才能收入高高。废话了这么多,其实因果推断更多的是在教授我们一种问题的分析的方法,好啦,话不多说,咱们先来看一个经典例子吧。
辛普森悖论
现实生活中观察各种变量之间的相关性,某些关系简单易懂,但是有些关系就复杂到无法理解,有些可能会给我们一些假的错觉,下面我们就来看一个经典的辛普森悖论。辛普森悖论通俗的讲是指两个变量X和Y在每个分组中的关系是正或是负,但是在总体中的关系会发生偏转。下面我们来看两张表。
| ID |
年龄 |
服药与否 |
健康指数 |
| 1 |
30 |
0 |
75 |
| 2 |
30 |
0 |
78 |
| 3 |
30 |
0 |
80 |
| 4 |
30 |
0 |
80 |
| 5 |
30 |
0 |
82 |
| 6 |
30 |
0 |
85 |
| 7 |
30 |
1 |
87 |
| 8 |
30 |
1 |
93 |
| 9 |
40 |
0 |
56 |
| 10 |
40 |
0 |
60 |
| 11 |
40 |
0 |
64 |
| 12 |
40 |
0 |
60 |
| 13 |
40 |
0 |
62 |
| 14 |
40 |
0 |
65 |
| 15 |
40 |
0 |
68 |
| 16 |
40 |
0 |
70 |
|
|
未服药 |
服药 |
康状况差 |
| 30岁 |
平均健康指数 |
80 |
90 |
10 |
| 40岁 |
平均健康指数 |
60 |
65 |
5 |
| 所有人 |
平均健康指数 |
73.3 |
72.1 |
-1.2 |
通过上面两张表能够看出,在30岁组中,服药者的平均身体健康指数比未服药的高10,但是40岁中服药者比未服药者要高5,但是如果在全局数据中服药者的健康指数却比未服药的低1.2.换言之,在分组数据,服药和健康指数是正相关,但是在全局数据中的结论确实相反的。那么怎么看待这个结论呢?
其实之所以会出现这样的结论的原因是:未服药的人大部分是30岁且健康的人,而服药者的大部分年龄是40岁且身体状况较差的人。因此在总体数据中,占大多数的30岁未服药的监控决定了总体的未服药的平均健康状况,所以出现了截然不同的效果。这个例子是想告诉我们相关关系不一定能反应因果关系。某些情况下,通过相关关系去推断因果关系还会矛盾,如果我们要从相关关系中识别因果关系就需要对相关关系产生的原因进行分析。
对于辛普森悖论,其实在推荐搜索中也是十分常见的。让我们看如下的例子。

可以看出,不管是男性用户还是女性用户都应该是B视频应该被推荐,但是通过全局数据看确是相反的结论。

可见,汇总实验对高维特征进行了合并,损失了大量的有效信息,因此无法正确刻画数 据模式。
变量关系路径图
路径图是因果关系分析中一个有效的辅助工具,它可以帮助我们分析因果关系,将复杂问题图形化,避免繁琐的公式。
路径主要分为三种,分别是因果路径、混淆路径以及对撞路径,接下来我们就一一来看看每种路径是什么意思。
因果路径
因果路径是从解释变量指向被解释变量的单向路径。
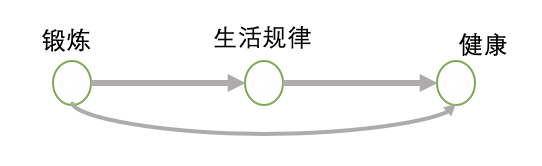
上图就是一个因果路径,第一条因果路径是锻炼直接影响健康,第二条就是锻炼影响生活规律从而影响健康。这里需要强调一下就是,如果两个变量之间存在因果路径,它们就存在相关关系,所以因果路径为开放路径。
混淆路径
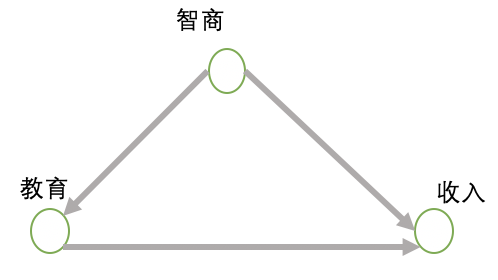
上图就是一个典型的混淆路径,智商会同时影响教育和收入,因此智商是一个混淆变量。教育和收入之间的两条路径:因果路径,教育->收入,混淆路径:
教育<-智商->收入。教育和收入的相关性可能是由于教育对收入的应该影响的,也可能是由于教育和收入同时受到智商的影响造成的。
对撞路径
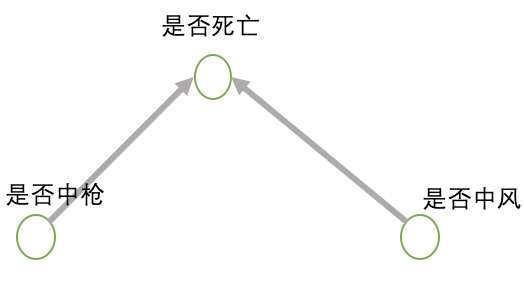
对撞路径是包含对撞变量的路径,对撞路径是被两个变量共同影响的变量。对撞路径不会造成两个变量的相关性。
因果推断估计偏差来源
估计变量之间的因果关系本质是找到两者的所有因果路径,同时除去非因果路径。原理虽然简单,但是实际研究中如果没有找到正确的路径关系就会产生偏差,这些偏差可以归纳为 混淆偏差、过度控制偏差、内生选择偏差。
混淆偏差
混淆路径会造成两个变量的相关性,但是整个相关性并非因果关系。因果关系分析中处理混淆路径的方法就是截断混淆路径。
我们用上面的例子来讲解这个混淆偏差。:因果路径,教育->收入,混淆路径:教育<-智商->收入。如果智商是能够被观测到的,要截取混淆路径,我们通过给定的智商来截断混淆路径。在回归分析中,给定某个变量的值就是控制某个变量。简而言之,混淆偏差指的是解释变量和被解释变量之间存在未截断的混淆路径,造成解释变量和被解释变量的相关性包含因果关系还包括非因果关系。
过度控制偏差
过度控制偏差是指控制了因果路径上的变量造成的偏差。例如我们要研究锻炼和健康的因果影响.如图1-1,显示锻炼与健康额两条因果路径,锻炼会直接影响健康,也会通过影响生活规律进而影响健康。如果我们控制了生活规律,就截断了其中一条因果路径,这种情况下,我们只估计了锻炼对健康的直接因果,而低估了生活规律的影响。
内生选择偏差
内生选择偏差也称为对撞偏差,前面提到的对撞路径是死路径,它不会造成两个变量相关。但是如果给定两个变量是对撞变量,会造成两个不相关的变量之间产生相关关系,这个错误就称为对撞偏差。
如图1-3,是否中风和是否中枪是无关变量,但是当是否死为“是”的时候,如果一个人的中风状态是“否”的时候,那么他的中枪状态应该是“是”,可见给定对撞变量D(是否死亡)为“是”时,中风状态和中枪状态为负相关。这就意味着死人样本中,中风状态和中枪状态是负相关,因此给定对撞变量,两个没关系的变量就有了关系。
内生选择偏差可以理解为,当给定两个变量共同的被解释变量时,两个变量之间会产生一个衍生路径。衍生路径造成了原本不相关的变量变为相关。
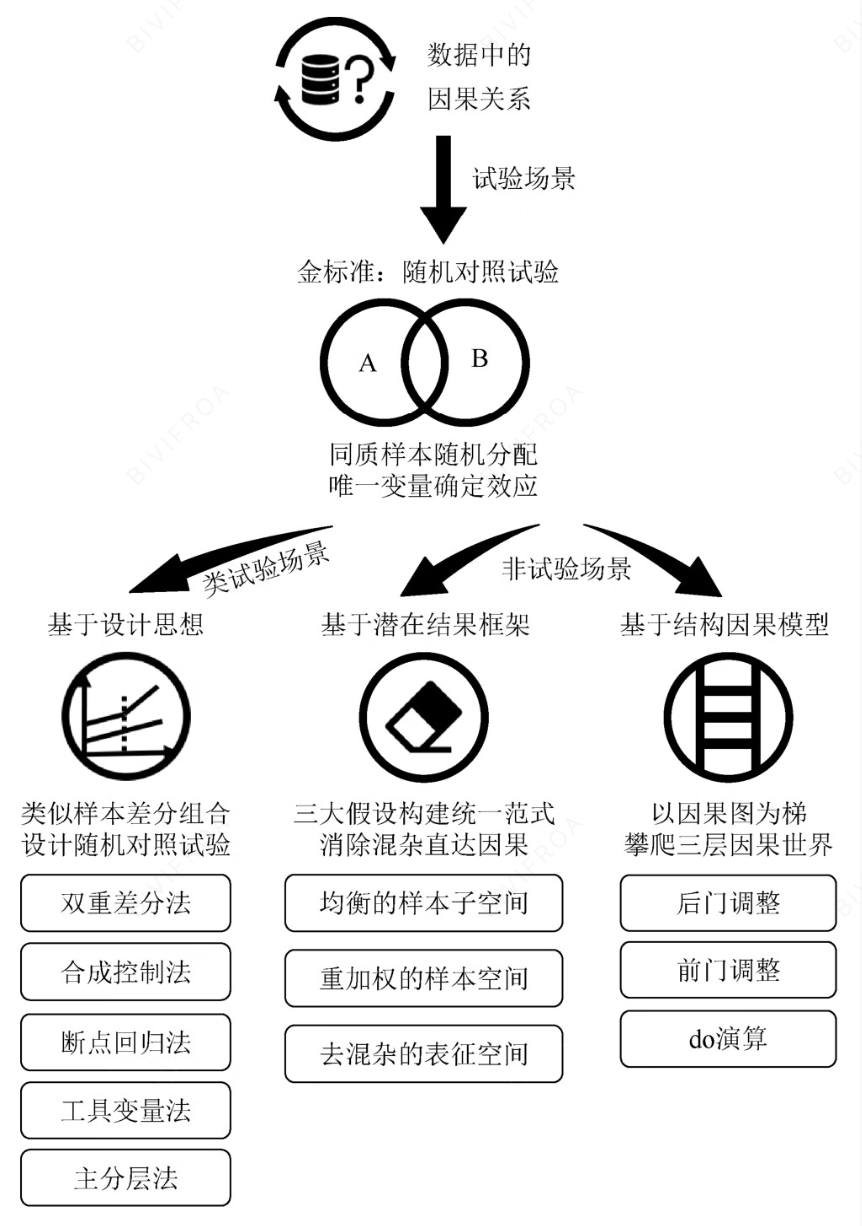
如何获得因果关系
下图给了一个宏观的路径和方法, 后续的章节中也会有方法的详细讲解。 可以先体系化串起来整个过程。
简而言之
不知道通过上面的介绍大家有没有对因果推断有了一点感觉,我们暂时将它当成一种分析方法,当我们做业务的时候,可以尝试去理解业务中出现的场景和模型中使用的特征,进而分析一个例子出现的场景是什么,也能为我们的特征工程提供一定支撑。