强化学习简介

首先我们来说下深度学习或者机器学习这个范畴，众所周知，深度学习此类学习方式是典型的端到端的学习方式，什么是端到端呢？就是我直接给你结果，你根据输入来告诉学习中间的过程，而中间的过程一般就是矩阵参数。

对比而言呢，强化学习其实一个序列决策，一听到这里第一个不同就是我们是在一个序列过程中做决策的。其实当年我有过这样一个疑问，如果我把强化学习的环境变成参数放到深度学习，从而变成一个端到端的学习可以吗？其实是这样的，当你把所有的上下文放到模型中学习的时候，这里有一个长期收益还是即时收益的问题，如果你只关心即时收益，那用深度是没有任何问题的，但是如果你关心长期收益，就需要按照强化的方式建模。所以强化学习一般来解决什么样的问题呢？咱们大部分看到的资料都是迷宫问题，就是放到迷宫里，给你试错机会，让你找到最优路径等等。

马尔可夫过程

在讲强化学习之前，让我们不得不先了解一下马尔可夫过程，马尔可夫过程其实也是对序列决策问题的一个简化，否则这个问题将会无比复杂。
接下来就介绍一下马尔可夫过程，马尔可夫相关理论其实还是比较庞大和复杂的，这里我们就介绍一丢丢就可以啦。

如果你当前的决策仅仅依赖上一个时刻的状态，而不是依赖整个历史状态，那么这个就是符合马尔可夫一个过程

$$P(S_{t+1}|S_t) = P(S_{t+1}|S_t) \tag{1.1}$$

凡是具有马尔可夫性的随机过程都称为马尔可夫过程。数学上经常使用一个元祖表示 $<S,P>$,这里S是有限数量的状态，P是状态转移的概率矩阵。

接下来我们来看下面这个图。

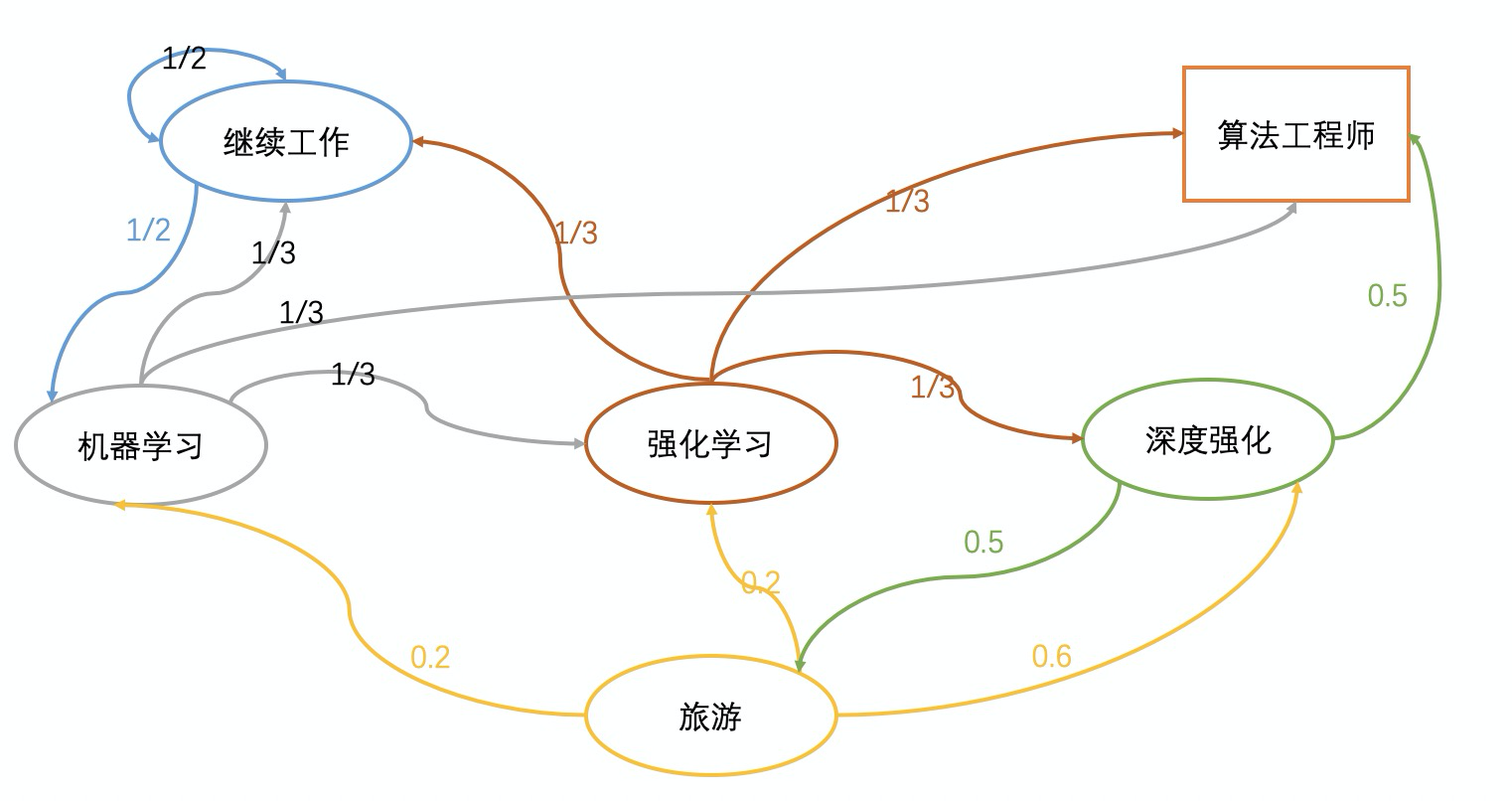
其中椭圆形和矩形是状态，而连线实际上是转移概率。
而转移矩阵就是如下。

$$\begin{bmatrix} 0.5 & 0.5 & 0 & 0 & 0 & 0\\ \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & \frac{1}{3}\\ \frac{1}{3} & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3}\\ 0 & 0 & 0 & 0 & 0.5 & 0.5\\ 0 & 0.2 & 0.2 & 0.6 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{bmatrix}$$

马尔可夫决策

马尔可夫决策是针对马尔可夫性的随机过程做出决策的过程。
一个马尔可夫决策过程由一个五元组构成$<S,A,P,R,\gamma>$。

• S表示状态集合。
• A表示动作集合
• P表示转移概率
• R表示回报函数
• $\gamma$表示衰减系数，也叫做折扣因子。使用折扣因子主要是为了计算当前状态的累积回报，将未来的立即回报也考虑进来。

相关的数学表达

$$P_{ss'}^{a}=P(S_{t+1}=s'|S_t=s,A_t=a) \tag{1.2}$$

公式1.2表示在s的状态下执行a的动作转移到s‘的概率。
当然某些时候P与动作无关。

$$P_{ss'}=P(S_{t+1}=s'|S_t=s) \tag{1.3}$$

如果在固定的策略$\pi$下，就可以表示为

$$P_{ss'}^{\pi}=\sum_{a \in A} \pi (a|s) P_{ss'}^{a} \tag{1.4}$$

公式1.4中的$\pi$可以理解成一个策略，当处于状态s的时候就使用动作a,公式1.5中的R是回报函数。

$$R_{s}^{a}=E[R_{t+1}|S_{t}=s,A_t=a] \tag{1.5}$$

讲到这里我们来回看上面的图，如果想计算“深度强化”转移到“强化学习”的转移概率如何计算呢？

$$P_{ss'}^{\pi}=\sum_{a \in A} \pi (a|s)P_{ss'}^{a} = 0.5*0.2+0.5*0=0.1 \tag{1.6}$$

这里我们可以稍作解释，如果想“深度强化”转移到“强化学习”，没有直接的边，只能从旅游这个状态转移，所以绿色的线先经过0.5的概率选择到旅游，然后通过0.2的概率转移到“强化学习”，另外的0.5*0表达的意思是转向算法工程师的边，因为这个边没有出度啦，所以只能是0.

那么我再来看下个问题，那“深度强化”转移到“强化学习”的回报是怎么来计算呢？我们来看下一个图。

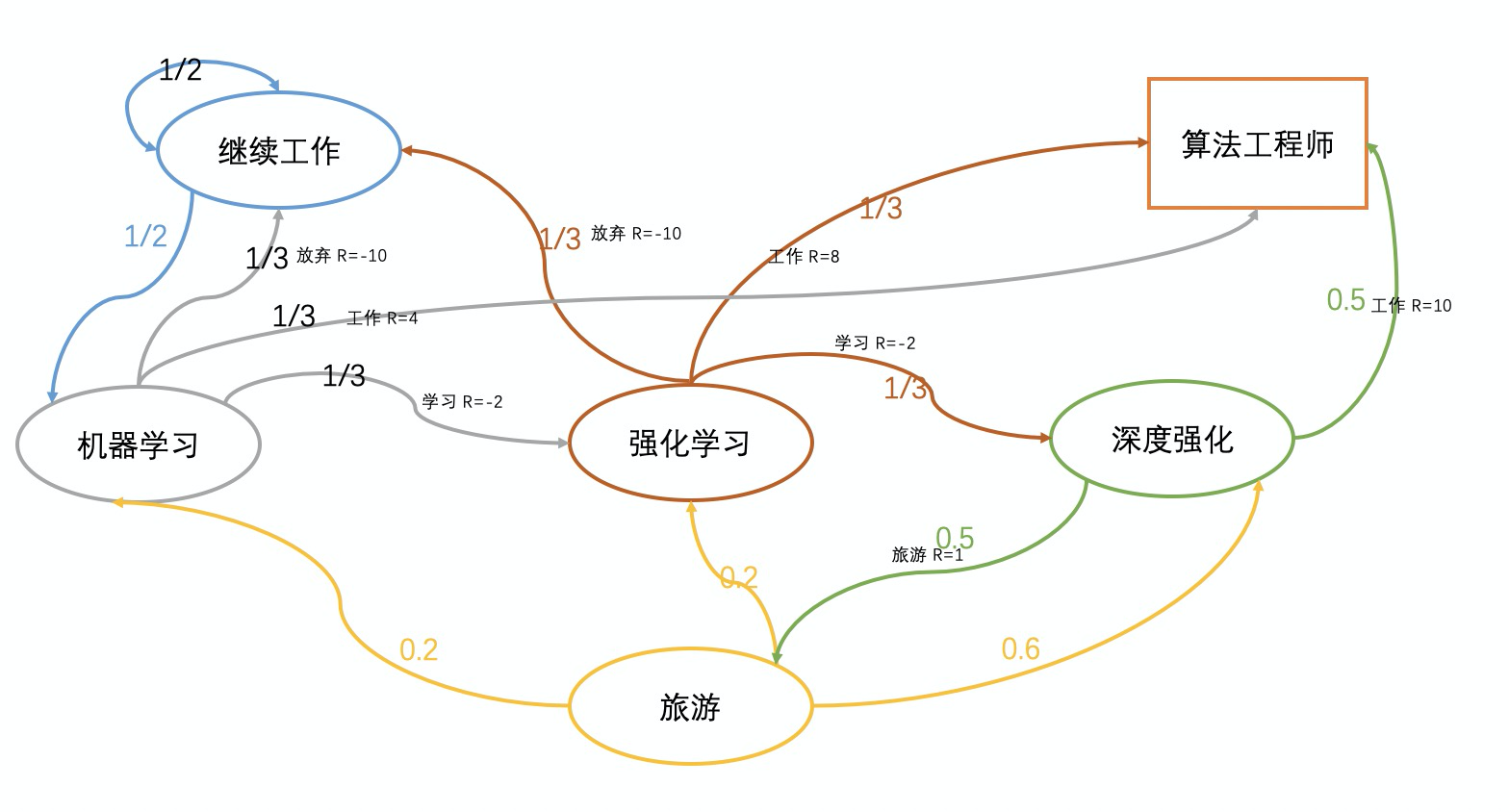
$$R_{s}^{\pi}=\sum_{a \in A} \pi (a|s)R_{s}^{a} = 0.5*1+ 0.5*10=5.5 \tag{1.7}$$

这个是时候你肯定会问，擦，这些R的值是哪里来的呀？这个例子就是想举个例子杜撰了一些R回报值，大家不必过于纠结这些细节。

环境引擎

通过上面的例子介绍了一些MDP的计算框架，接下来的章节中就来分别看看MDP的组成部分。

状态空间

状态空间是描述环境的重要特征，例如经典的格子世界，格子的编号就是状态的一种表达，但是实际的生产应用中，状态空间往往用一个集合表示，用来描述整个环境，例如【温度，降雨量，。。】

动作

另一个重要的组成部分是动作集合，在一个状态下，采用什么样的动作往往是影响环境的机制，动作空间往往是有限的，与状态变量不同的是组成动作的数量可能不是常数，例如是一个连续的值。

转换函数（转移概率）

环境对动作的响应方式呗称为状态转移概率，也就是转换函数，经常使用(s,a,s’)映射的一个概率，也就是传入一个状态s，使用动作a，获得另一个状态s‘的概率，例如1-2中，同一个椭圆实体对外转移同颜色的边的概率相加是1

奖励

奖励经常是在学习中是扮演反馈的角色， 当你在s状态使用动作a，变成状态s’，反馈应该是多少R（格子世界中是离终点跟更近啦，还是更远啦）。

折扣因子

折扣因子是权衡当前收益和未来收益的手段，如下公式中，随着时间的推移，越往后收益越打折扣。也就是传说中的未来是不确定的，别太看重它

$$G_{t}=R_{t+1}+rR_{t+2}+r^{2}R_{t+3}...$$

综上所述

这里咱们总结一下吧，大概用一个例子讲了一下强化学习的概念。这些概念可能在以后的学习中也会经常使用。