归一化方法
我们做机器学习的时候,都会假设数据的原始分布是独立同分布的数据分布(IID) (为什么呢?),但是对于神经网络来讲就层级的网络结构使得底层参数对高层级的输出分布影响很大,所以很难满足这个假设。对于这个问题我们一般引入一个归一化的方法,实际上是通过采取不同的变换方式使得各层输入数据近似满足独立同分布的假设。
为什么输入数据要满足独立同分布呢?
是独立同分布: 在概率统计理论中,如果变量序列或者其他随机变量有相同的概率分布,并且互相独立,那么这些随机变量是独立同分布。
独立:每次抽样之间没有关系,不会相互影响
举例:给一个骰子,每次抛骰子抛到几就是几,这是独立;如果我要抛骰子两次之和大于8,那么第一次和第二次 抛就不独立,因为第二次抛的结果和第一次相关。
同分布:每次抽样,样本服从同一个分布
举例:给一个骰子,每次抛骰子得到任意点数的概率都是六分之一,这个就是同分布
独立同分布:i,i,d,每次抽样之间独立而且同分布
了解完独立同分布,那么就不难理解,我们机器学习为什么需要这个样的假设,机器学习解决的问题大部分是根据历史数据对未来的一个估计,如果历史数据的分布被我们学到,那么我们预测未来就显得格外简单。
batch normalization (批次归一化)
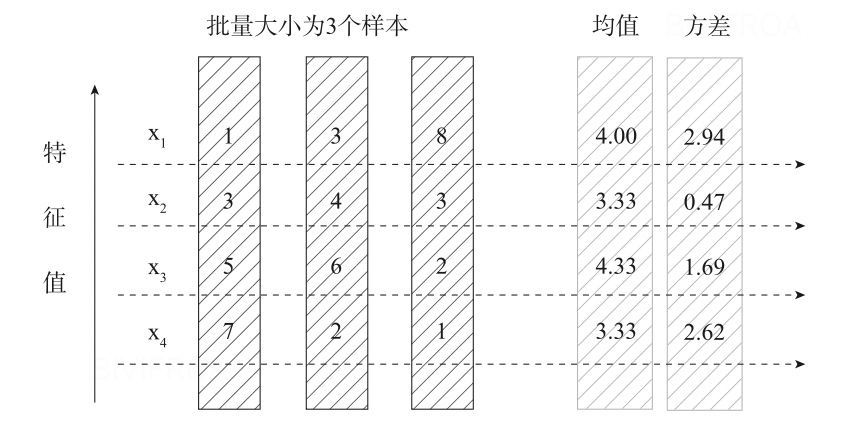
目前我们一般使用分批次梯度迭代的方式进行优化参数,会将我们的数据分为若干组,按组来更新参数,一组中的数据共同决定梯度的方向,另一方面也能减少计算量。
batch normalization也是比较常用的归一化方法,常用在卷积以后,用于重新调整分布。
假设某一个层批次的输入数据X=(x0,x1,...,xn)其中每个xi是一个样本,而n是样本总数。
μx=n1i=1∑nxi(1.1)
σx2=n1i=1∑n(xi−μx)2(1.2)
xl=σx2+ϵxi−μx(1.3)
layer normalization(层归一化)
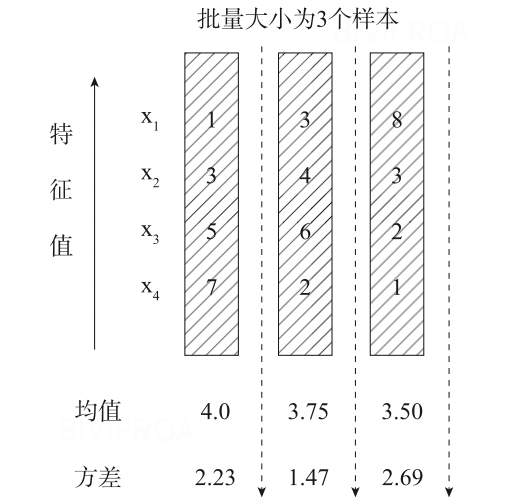
batch normalization是一个非常常用的方法,对于网络结构固定的场景确实也能发挥很大的作用,但是对于网络深度不确定的情况下就很难起到作用,例如RNN 。
这个时候我们就要引进另一个归一化的方法,layer normalization希望大家能记得每个归一化的方法都有自己的场景,layer normalization仅仅考虑当前层的均值和方差,实际方法和上文提到的方法类似。对于相似度相差较大的的特征,layer normalization可能降低模型的表达能力,如果这样还是使用batch normalization比较好。
拓展
除此以外还有weight normalization和group normalization等方法,需要大家自己深度探索。