今天介绍的是TCN模型,在介绍这个模型的过程中,会介绍很多额外的小知识点,个人觉得还是很有用的。下面咱们就来介绍TCN模型。
TCN模型
先来看问题定义,对于时序问题还是老生常谈的输入输出形式。 x=[x0,x1,...xT], 作为输入的值, 输出就是对应的y=[y0,y1,...,yT]作为输出。那么TCN模型是如何组织模型结果的呢?
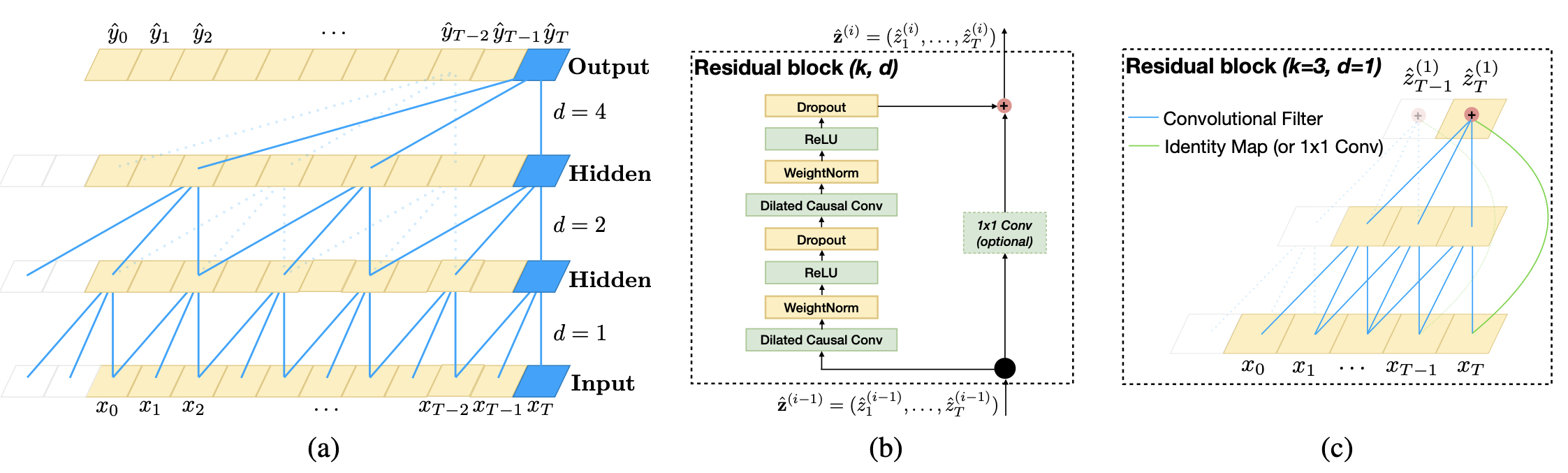
刚开始的时候作者使用了一个全连接网络做因果卷积,对输入的时序做1D的卷积操作。这里要介绍一下什么是因果卷积(Causal)。
因果卷积(Causal)
如下图1-1就是一个典型的因果卷积形式,当前的输出依赖中间几层的隐层输入, 看起来是一个层层归纳的过程。
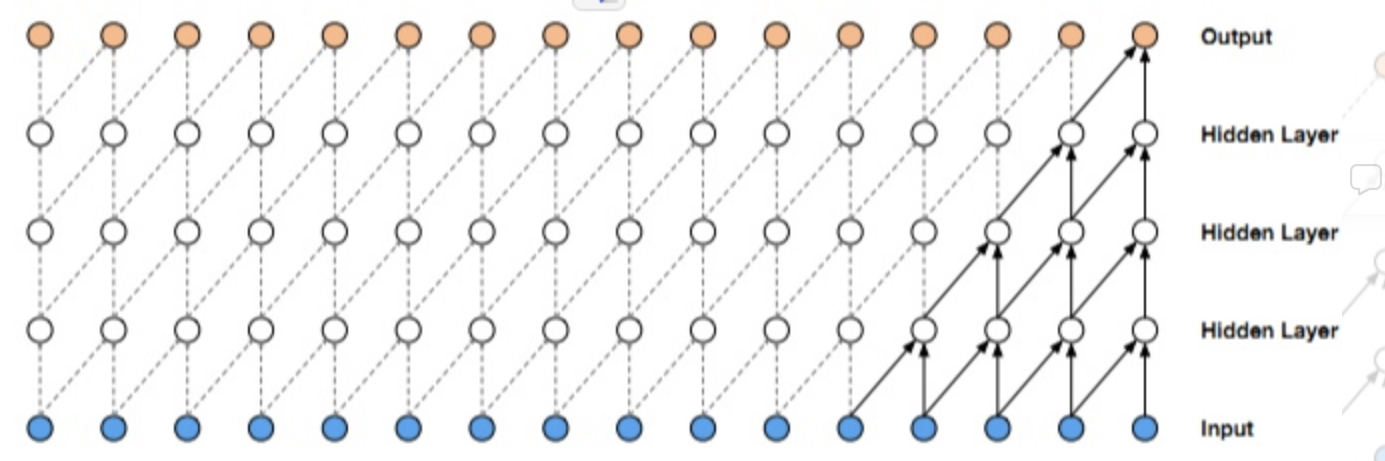
使用这种卷积能够将信息充分利用起来,不遗漏任何低阶以及高阶特征。TCN的表达方式也比较简单TCN = 1D FCN + causal convolutions.a 1D fully-convolutional network (FCN)。
之所以使用这种类型的CNN,原因是原始的CNN是不能学习序列特征的,使用因果卷积,其作用就是对与序列问题的学习。将一个预测值通过几个输入层层归纳总结并给出结果,适合序列数据的学习。
扩展卷积(Dilated)
但是单纯使用上面的结构也是存在一部分问题的,特别是当前的数据依赖更长时间的历史,这种结构就难以刻画。这个时候就引进了扩展卷积,也称为空洞卷积。如图1-2

上图是在图像数据中的使用,能够有效的降低计算量的情况下不会丢失准确性。是时序模型中,会有一点不同,就如上图1-0中的(a)图,在一个维度上进行层层的间隔采样达到空洞卷积的作用,当然在TCN中不是为了性能,而是观测增大感受野,获取更长时间历史的特征。
残差网络结构
在TCN网络中也是用残差的网络结果,也是为了保证长期的历史数据不丢失的问题。如图1-0中的(b)图, 在使用了几个扩展卷积的过程中,提供一个直接链接结果的通路(这个是残差的结构),最后合并成最终结果。 这里看到一个1×1的卷积核。在TCN中只是为了保证维度对齐的作用,而本文想介绍一下1×1的卷积核的作用。
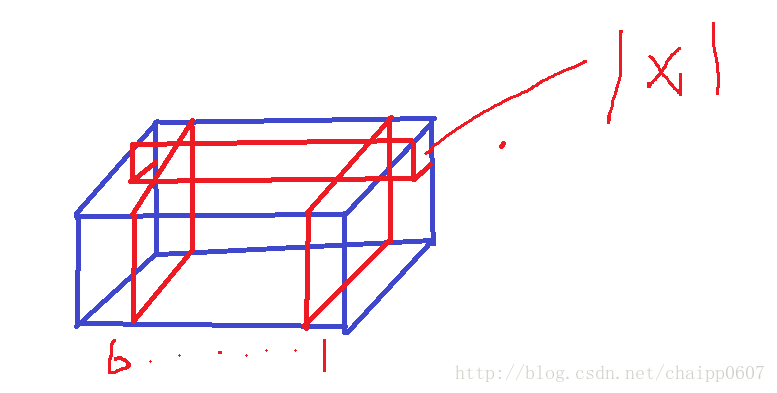
这里咱们再盗个图,对于下面这个立方体,假如是一个M×M×Q的结构,如果我希望构造一个M×N×(Q−1)的结构如何构建呢? 方法是如图,我通过一个1×1×Q, 然后每卷积一次就产生一个M×N×1的结构,然后想链接几个就能把这个M×M×Q的结构降维到多少。 这里说一下1×1的卷积核除了有降低维度的作用,其实也有一个意图是想学习通道之间的关系。这一点也是十分重要的,类似的我也能够通过1×1的就卷积核做升维。
如图0-1中的©就是整个网路网络的结构,通过这么多网络的学习,发现大家还是对时序问题下了功夫的,一行时序问题,使用这么多的参数和算力,具体使用的场景就要看看工作了。
论文地址: TCN