时间序列预测(一)--DeepAR模型

今天咱们就来看看第一个时序模型，可能有些同学都没有听说过这个模型，这个模型还是相对复杂的，接下来咱们来看看这个模型。对于一般的时序任务，大家一般会想到NLP中的一些序列模型，LSTM、GRU等模型，这类方法都是给出一个确定的预测值，接下来咱们要介绍这个模型有一点不一样，DeepAR模型并不是直接简单地输出一个确定的预测值，而是输出预测值的一个概率分布，这样做其实有点好处，咱们给出的预测值其实很难让你感知到这个预测值的置信度，而给出一个概率分布很多场景用处会更大一些。

DeepAR

现在咱们来看看这个模型的细节。首先咱们来看下模型的一些符号表示。

$z_{i,t}$ 表示第i个时间序列的第t个值， $t_{0}$ 表示预测的开始时刻，所以这个问题就可以描述成已知 $z_{i,0:t_{0}}$ ,求后续的时间序列 $z_{i,t_{0}:T}$ 的问题啦。
咱们把这个问题描述成一个似然问题是怎么样的呢？

P(z_{i,t_{0}:T}|z_{i,1:t_{0}-1},x_{i,1:T}) \tag{1.1}

就是咱们已知了1到 $t_{0}$ 时刻的数据，和 $t_{0}$ 到T时刻的协变量(包括节假日、活动日等)信息，最大概率的 $z_{i,t_{0}:T}$ 分布是什么的问题？然后转化成一系列的似然因子的乘积的形式如下。

Q_{\Theta}(z_{i,t_{0}:T}|z_{i,1:t_{0}-1},x_{i,1:T})\\ =\prod_{t=t_{0}}^{T} Q_{\Theta}(z_{i,t}|z_{i,1:t-1},x_{i,1:T}) \\ =\prod_{t=t_{0}}^{T} \iota(z_{i,t}|\theta(h_{i,t}, \Theta))

其中 $h_{i,t}=H(h_{i,t-1},z_{i,t-1},x_{i,t},\Theta)$ 其中的H是一个多层自循环网络的学习结果，而h是上层学习产生的中间变量，然后咱们再按照概率的思想分析这个模型，观测序列是 $z_{i,t-1}$ 是模型的输入，之前的隐状态是 $h_{i,t-1}$ ,然后似然估计是 $\iota(z_{i,t}|\theta(h_{i,t}))$ ,且是一个固定的分布，当学习使用循环网络学习到的 $\theta(h_{i,t},\Theta)$ 学习收敛以后，这个一部分后面详细介绍。整个的模型如下

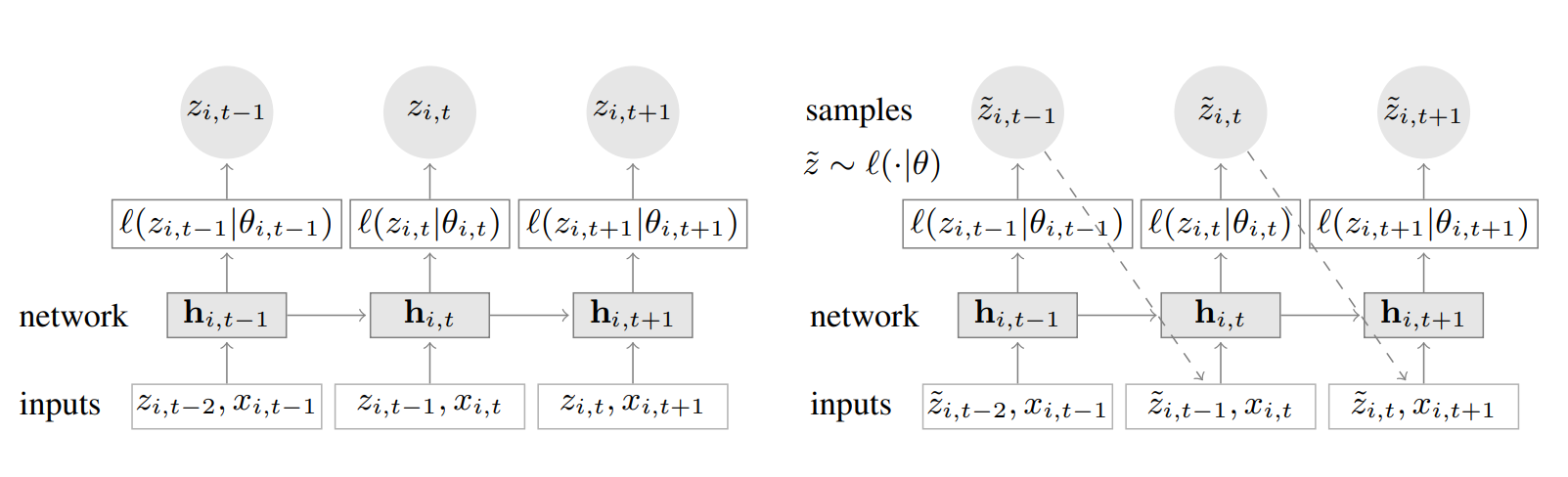
左边的是训练的过程，右边的是预测过程，可以发现多了一条虚线，这个虚线就是说当你前一个结果预测出来以后，要放到后面的网络中继续学习。

似然函数

对于上文面模型的结构中有一个结构是 $\iota(z_{i,t}|\theta)$ ，这个函数是一个似然估计，某种意义上应该符合原始的数据分布。对于真值的预测，假设原时间序列是一个高斯分布。那么会有如下的预测表达形式。

\iota(z|\mu,\sigma)=(2 \pi \sigma^{2})^{-\frac{1}{2}} exp(-(z-\mu)^{2}/2 \sigma^{2}) \tag{2.1}

然后这个分布中的 $\mu, 、\sigma$ 通过模型的参数进行拟合。

\mu(h_{i,t})=W_{\mu}^{T} h_{i,t}+b_{\mu} \\ \sigma(h_{i,t})=\log(1+exp(W_{\sigma}^{T}+b_{\sigma}))

对于计数预测就是默认负二项式分布，这里就不过多介绍啦。可以看出这里还是和咱们以前了解的模型还是不一样的，通过描述一个分布来描述一个预测任务，这个还是比较新颖的。

训练

对于训练的损失也有一点特殊，最后实际上需要优化如下的损失函数。

Loss= \sum_{i=1}^{T} \sum_{t=t_{0}}^{T} \log \iota(z_{i,t}|\theta(h_{i,t}))

最后需要学习一个参数集合，最大化以上损失函数的最大似然估计。这个对应下面的代码咱们可以看看这个点。

代码

接下来咱们来看看经典的实现过程，这里有很多的开源工具，以下代码只是为了让大家看清楚它的实现过程。

import tensorflow as tf
import tensorflow_probability as tfp

class DeepAR(tf.keras.models.Model):
  """
  DeepAR 模型
  """
  def __init__(self, lstm_units):
      super().__init__()
      # 注意，文章中使用了多层的 LSTM 网络，为了简单起见，本 demo 只使用一层
      self.lstm = tf.keras.layers.LSTM(lstm_units, return_sequences=True, return_state=True)
      self.dense_mu = tf.keras.layers.Dense(1)
      self.dense_sigma = tf.keras.layers.Dense(1, activation='softplus')

  def call(self, inputs, initial_state=None):
      outputs, state_h, state_c = self.lstm(inputs, initial_state=initial_state)

      mu = self.dense_mu(outputs)
      sigma = self.dense_sigma(outputs)
      state = [state_h, state_c]

      return [mu, sigma, state]

def log_gaussian_loss(mu, sigma, y_true):
  """
  Gaussian 损失函数
  """
  return -tf.reduce_sum(tfp.distributions.Normal(loc=mu, scale=sigma).log_prob(y_true))

上文log_gaussian_loss定义损失函数的时候，通过训练好的参数构造一个高斯分布，然后通过y_true访问在这个分布中的概率，这行代码的意思是，我构造一个分布让当前的真值取值概率最大，那么我就知道当前这个预测值的分布，从而能够给出一个完整的估计。下面是这个函数的调用方法。log_prob 得到从正态分布中选择一个值的概率。

LSTM_UNITS = 16
EPOCHS = 5
# 实例化模型
model = DeepAR(LSTM_UNITS)
# 指定优化器
optimizer = tf.keras.optimizers.Adam()
# 使用 RMSE 衡量误差
rmse = tf.keras.metrics.RootMeanSquaredError()
# 定义训练步
def train_step(x, y):
  with tf.GradientTape() as tape:
      mu, sigma, _ = model(x)
      loss = log_gaussian_loss(mu, sigma, y)
  grads = tape.gradient(loss, model.trainable_variables)
  optimizer.apply_gradients(zip(grads, model.trainable_variables))
  rmse(y, mu)

这里需要注意一下，rmse是衡量损失的，但并不是损失函数，如论文所讲。

原文地址: DeepAR

支付宝捐赠

微信捐赠

时间序列预测(一)--DeepAR模型

DeepAR

似然函数

训练

代码

喜欢这篇文章？打赏一下作者吧

相关推荐

Your browser is out-of-date!