时间序列预测(二)--N-BEATS模型

今天咱们来介绍一个纯时序模型，N-BEATS模型，直接开门见山看看模型的机构，然后对着模型解读。

N-BEATS模型结构

图1.1
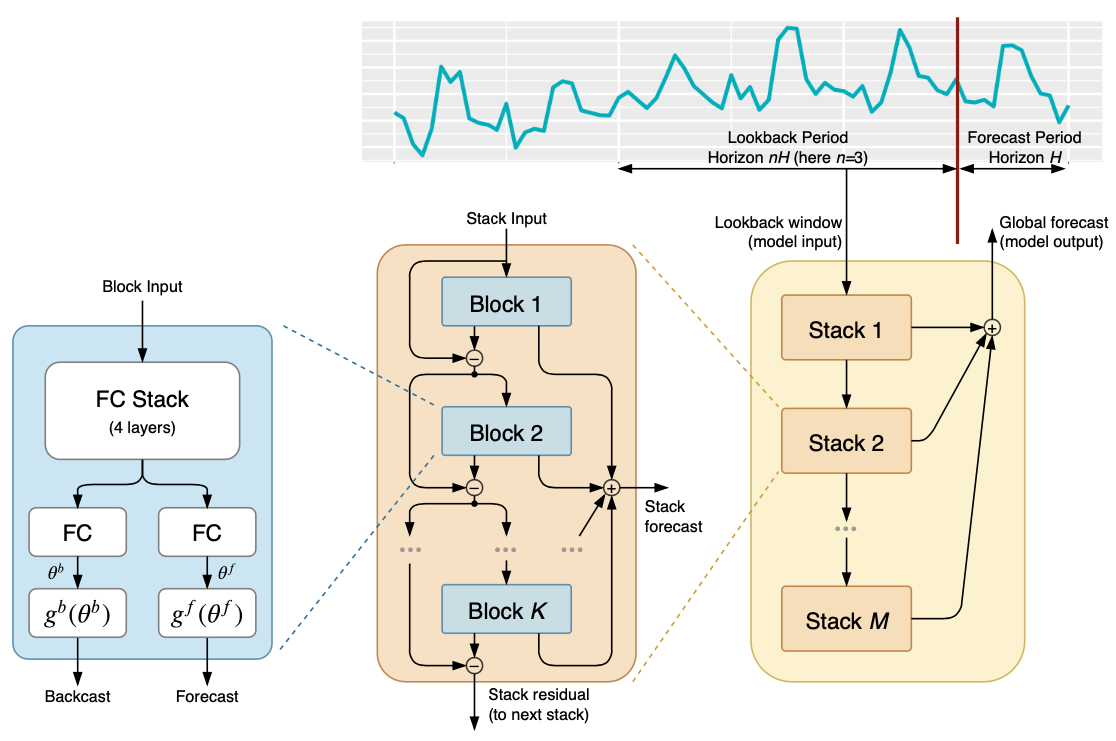
图1.1就是N-BEATS模型的结构，看起来比较复杂，咱们拆开来看。首先来看模型的输入，输入的是观测序列 $[y_{1},...,y_{T}]$ , 输出是预测数据 $[y_{T},...,y_{T+H}]$ , 这里在原文中描述T=nH, n一般取2到7。

看上图的模型主要有几个结构，分别是stack、block。多个block组成1个stack。输入的数就是之前一段时间的观测数据。

图1.2

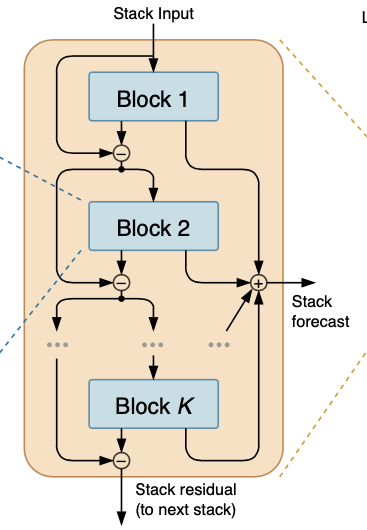
上图是一个stack结构，第一个block的输入是观测序列x，然后经过一个block会输出两个向量，分别是backcast $\vec{x}$ ,和长度为H的预测向量 $\vec{y}$ ，后面block的输入是前面block的输出。

一个Block里面由两部分构成，如下图。

图1.3
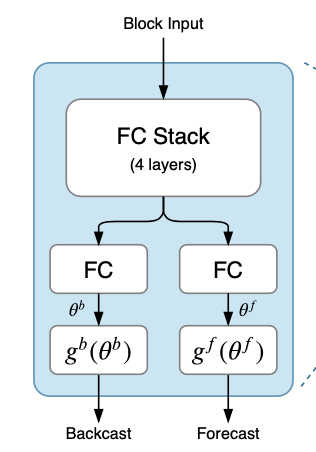
第一部分是全连接层生成 $\theta_{b}$ 和 $\theta_{f}$ ，这里的线性层是一个简单的投影。其中FC Stack如下

h_{1}=FC_{1}(x) \\ h_{2}=FC_{2}(h_{1}) \\ h_{3}=FC_{3}(h_{2}) \\ h_{4}=FC_{4}(h_{3}) \\ \theta_{f}=w h_{4}

其中FC是一个标准的全连接层，激活函数RELU。w是需要学习的权重。
第二部分是由 $g^{b}(\theta_{b})$ 和 $g^{f}(\theta_{f})$ 组成，接受上文的 $\theta_{f}、\theta_{b}$ ，用于预测前向序列y，和后向序列x。

y=g^{f}(\theta_{f}) \\ x=g^{b}(\theta_{b}) \\

通过预测 $\theta_{f}$ 来优化预测y的准确性，而预测x的作用是移除输入中对预测结果没有帮助的成分，帮助下游模块更好的预测。然后使用双残差的结构。这里需要注意一下，前4个全连接层是共享的，只有到最后产生前后向参数的时候才引入独立的FC，从而能够通过历史的残差提升对预测的数据预测精度

x=x_{t-1}-x_{t} \\ y= \sum y_{i}

输出的x不断求残差，然后每次输出的y在最后聚合以后变成实际的预测值。那么就搞定了预测任务。

可以发现N-BEATS模型有一个比较好的思路是不仅预测后续的n个值，同时将过去的可观测值也当成一个输入，这样其实是更能让模型的准确率提升的，也是一个比较有意思的思路。希望在后续的工作中借鉴。

原文地址: N-BEATS