对于梯度相信大家都不陌生，咱们经常把它翻译成导数。那么咱们就先来看看在梯度下降中导数是怎么起到作用的。

导数

一阶导数十分好理解，一阶导数是表示原函数的一个斜率信息，而二阶导数是告诉我们一阶导数随着输入是如何变化的，可以认为二阶导数是对曲率的衡量。如果这样的函数具有零二阶导数，那就没有曲率，也就是一条完全平坦的线，仅用梯度就可以预测它的值。也就是是当学习率是$\alpha$的时候，每次沿着梯度负方向移动$\alpha$的时候，代价函数也移动$\alpha$。但是如果二阶导数是负数的时候，函数曲线向下凹陷(向上凸出)，因此代价函数将下降得比$\alpha$下降的多，如果二阶导数是正的，函数 曲线是向上凹陷(向下凸出)，因此代价函数将下降得比$\alpha$移动的少。

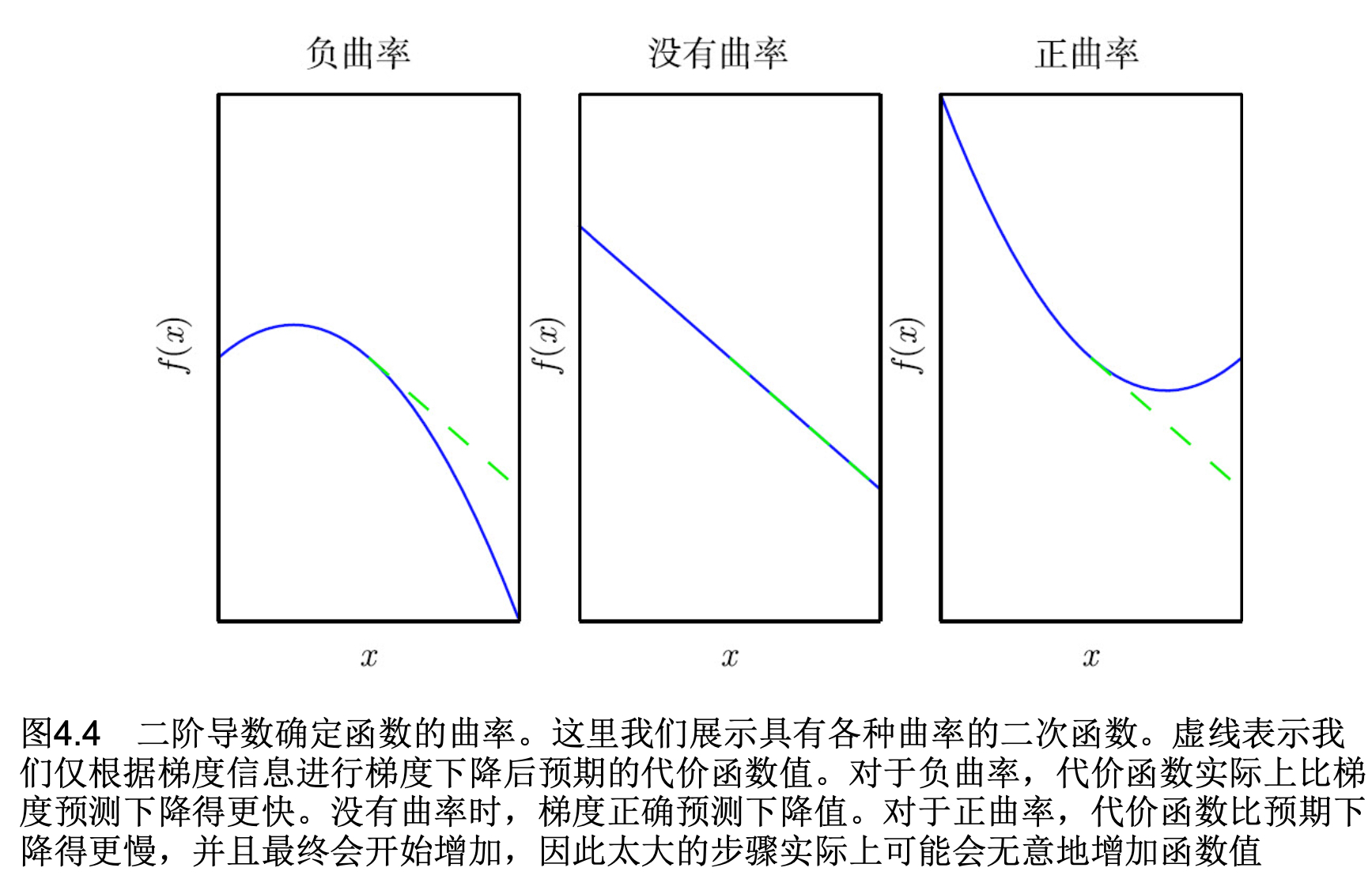
通过上面这个图能够看的十分清楚，梯度与曲率的关系。其实二阶导数表达的是每次梯度下降对损失函数变化的预期。

Hessian 矩阵

当我们的函数具有多维输入时，二阶导数也有很多。我们可以将这些导数合并成一个矩阵，称为Hessian矩阵。

$$H(f)(x)_{i,j}=\frac{\partial^{2}}{\partial x_{i} \partial x_{j}} f(x)$$

微分算子在任何二阶偏导连续的点处可交换，也就是它们的顺序可以互换.也就是说Hessian矩阵是一个对称矩阵。因为Hessian矩阵是实对称的，我们可以将其分解成一组实特征值和一组特征矢量的正交基。在特定方向d上的二阶导数可以写成$d^{T}Hd$.用到下面的泰勒展开中。
我们可以通过(方向)二阶导数预期一个梯度下降步骤能表现得多好。看下面这个推导过程。当前点$x_{0}$处的函数f(x)的二阶泰勒展开如下

$$f(x)=f(x_{0})+(x-x_{0})^{T}g+\frac{1}{2}(x-x_{0})^{T}H(x-x_{0})$$

其中g是梯度，H是$x_{0}$点的Hessian。如果使用学习率$\alpha$,那么新的点x将会是$x_{0}-\alpha g$。

$$f(x_{0}-\alpha g)=f(x_{0})-\alpha g^{T}g+\frac{1}{2} \alpha g^{T}H g$$

其中上面的三项分别是，函数原始值，函数斜率导致的预期改善和函数曲率导致的矫正。这里有个比较有意思的事情，当最后一项太大的的时候，梯度下降是可能向上移动的。当$g^{T}H g$为0或者为负数的时候，使用$\alpha$将会永远让f下降。在实际中，泰勒级数不会在$\alpha$大的时候也保持准确，因此这种情况下就要采用启发式的选择（蒙）。当$g^{T}H g$为正的时候，最优步长为

$$\alpha=\frac{g^{T}g}{g^{T}Hg}$$

最坏的情况下,g和H的最大特征值$\lambda_{max}$对应的特征矢量对齐，则最优步长是$\frac{1}{\lambda_{max}}$,当我们要最小化的函数能用二次函数很好地近似的情况下，Hessian的特征值决定了学习率的量级。

进阶

二阶导数还可以用于确定一个临界点是否是局部极大点、全局极小点或鞍点。回想一下当f’(x)=0, f’‘(x)>0的时候，意味着f’(x)会随着我们移向右边而增加，移向左边而减小。也就是$f'(x-\alpha)<0,f'(x+\alpha)>0$。换句话说，当我们移向右边，斜率开始指向右边的上坡;当我们移向左边，斜率开始指向左边的上坡。那么咱们能够得出如下的结论，当f’(x)=0, f’‘(x)>0的时候，x是一个全局 极小点。当f’(x)=0, f’‘(x)<0的时候，x是一个局部极大点。这就是所谓的二阶导数测试 (second derivative test)，但是当 f’'(x)=0的时候，测试是不确定的，这种情况下x可以是一个鞍点或平坦区域的一部分。

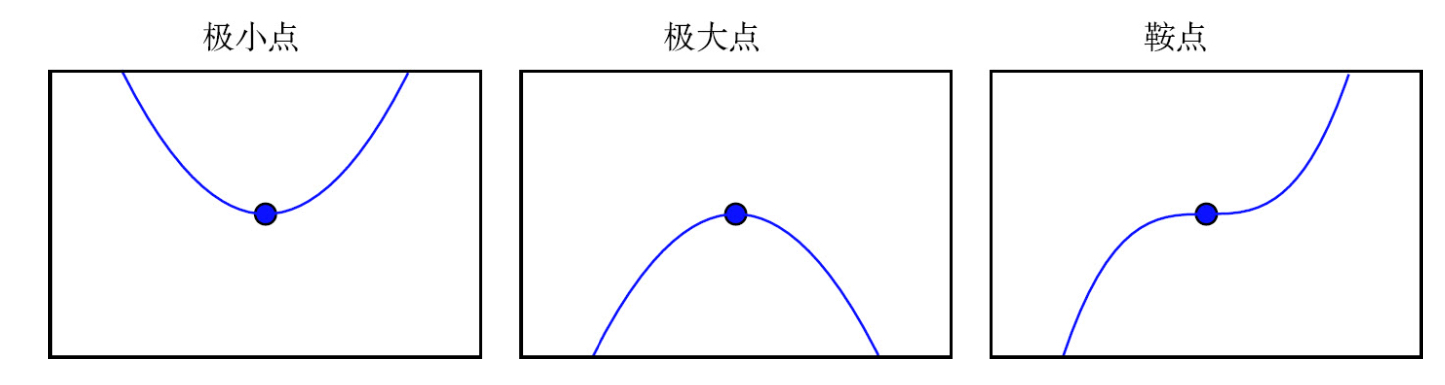
当Hessian是正 定的(所有特征值都是正的)，则该临界点是全局极小点。因为方 向二阶导数在任意方向都是正的。同样的，当Hessian是负定的(所有特征值都是负的)，这个点就是局部极大点。在多维情况下，实际上我们可以找到确定该点是否为鞍点的积极迹象(某些情况下)。如果Hessian的特征值中至少一个是正的且至少一个是负的，那么 x 是f某个横截面的局部极大点，却是另一个横截面的全局极小点，如下图表达是函数$f(x)=x_{1}^{2}-x_{2}^{2}$。

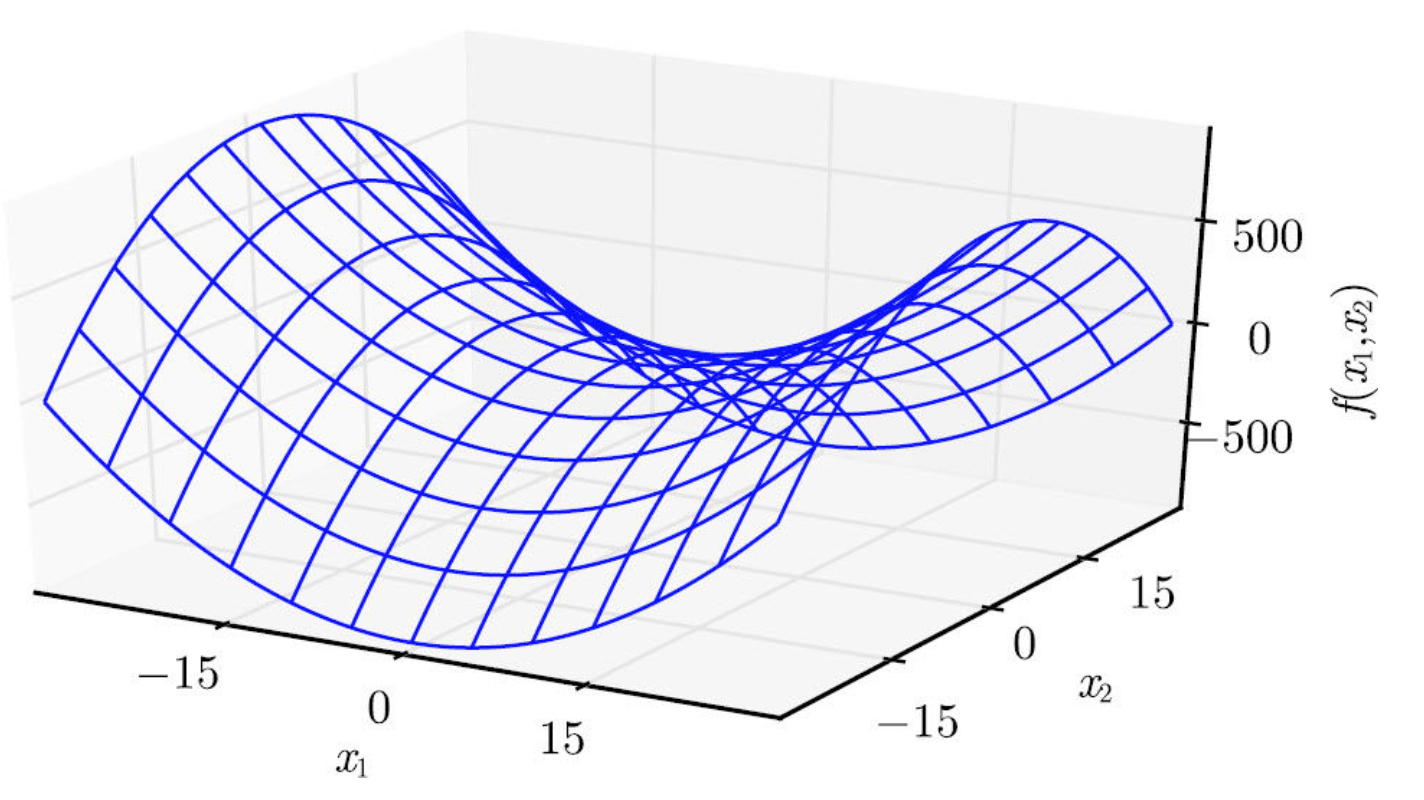
仅使用梯度信息的优化算法称为 (first-order optimization algorithms)，如梯度下降。使用Hessian矩阵的优化 算法称为 (second-order optimization algo- rithms)(Nocedal and Wright，2006)，如牛顿法。