Google 的两位创始人都是斯坦福大学的博士生,他们提出的 PageRank 算法受到了论文影响力因子的评价启发。当一篇论文被引用的次数越多,证明这篇论文的影响力越大。正是这个想法解决了当时网页检索质量不高的问题。
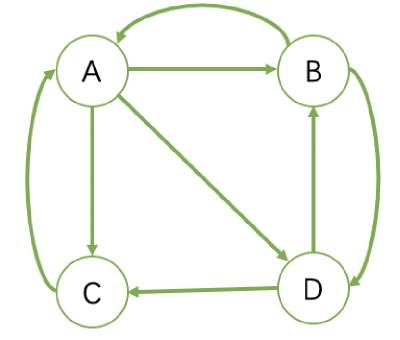
Page Rank 的计算过程
最初pagerank 算法是解决搜索引擎中的页面权重问题的,简而言之就是一个网页的权重多少是取决于这个网页的入链接和出链接的。
PR(u)=v∈Bu∑L(v)PR(v)(1.1)
u 为待评估的页面, Bu 为页面u 的入链集合。针对入链集合中的任意页面 v,它能给 u 带来的影响力是其自身的影响力 PR(v) 除以 v 页面的出链数量,即页面 v 把影响力 PR(v) 平均分配给了它的出链,这样统计所有能给u 带来链接的页面 v,得到的总和就是网页 u 的影响力,即为 PR(u)。
B 有两个出链,链接到了 A 和 D 上,跳转概率为 1/2。
我们能够根据图的拓扑结构获取整个图的转义矩阵M
M=⎝⎜⎜⎜⎛03131312100211000021210⎠⎟⎟⎟⎞
初始影响力我们就用一个平均分布就可以。
w0=[41,41,41,41]
w1=Mw0=[259,255,255,255]
依次类推,我们用M去乘以w1,w2,直到w收敛。
import numpy as np
transfer_mat = [[0.0, 1.0 / 2, 1, 0.0],
[1.0 / 3, 0, 0, 1.0 / 2],
[1.0 / 3, 0, 0, 1.0/2],
[1.0 / 3, 1.0 / 2, 0, 0]]
transfer_mat = np.array(transfer_mat)
prob = np.array([[0.25, 0.25, 0.25, 0.25]])
prob = prob.T
n = 100
while n > 0:
prob = np.matmul(transfer_mat, prob)
print prob
n -= 1
print prob
等级泄露(Rank Leak)
不知道有没有发现,如果当图中的有一个节点没有出度,最后将吸收吸收所有的入链的权重,最后导致整个网络为0。
等级沉没(Rank Sink)
如果一个网页只有出链,没有入链,计算的过程迭代下来,会导致这个网页的 PR 值为 0(也就是不存在公式中的 V)。
为了解决简化模型中存在的等级泄露和等级沉没的问题,拉里·佩奇提出了 PageRank 的随机浏览模型。他假设了这样一个场景:用户并不都是按照跳转链接的方式来上网,还有一种可能是不论当前处于哪个页面,都有概率访问到其他任意的页面,比如说用户就是要直接输入网址访问其他页面,虽然这个概率比较小。
所以他定义了阻尼因子 d,这个因子代表了用户按照跳转链接来上网的概率,通常可以取一个固定值 0.85,而 1−d=0.15 则代表了用户不是通过跳转链接的方式来访问网页的,比如直接输入网址。
PR(u)=N1−d+dv∈Bu∑L(v)PR(v)(1.2)
其中 N 为网页总数,这样我们又可以重新迭代网页的权重计算了,因为加入了阻尼因子 d,一定程度上解决了等级泄露和等级沉没的问题。