jpeg压缩算法
jpeg可能是理工男比较常见的图片格式,而jpeg是一种带压缩的算法,并是不原始图片,那么问题来了,jpeg的压缩算法是怎样的呢?本文将会结合实例讲解这个问题。
jpeg图片对大家来说可能是再常见不过了,我原来就比较肤浅了,认为jpeg只是一种图片格式而已,并没有深入了解每种图片格式之间的存储策略和侧重点。最近用到一个CNN的算法,恰好是自编码图片,所以理所应当的选择了jpeg的保存方式,好吧入坑了。因为不了解这种格式的存储协议,以为都是一样的点矩阵而已,殊不知jpeg里面是有压缩算法支撑的,导致训练是一种数据,预测的时候我想用点矩阵效果奇差无比,然后就。。。。背景交代一下,其实也是给大家交代一个问题,就是你使用一个东西的时候一定要有相应的考虑,要不前期越无脑后期越伤脑。好,咱们就废话不多说,来看看jpeg是如何压缩的图片。
jpeg压缩
JPEG能够获得如此高的压缩比是因为使用了有损压缩技术,所谓有损压缩就是丢弃一些不重要的信息,然后存储的空间会相应的减少。例如我们想存储一个数字2.00000001,这个时候我们其实仅仅存储一个2就够了,至于后面的信息不容易被用户感知直接丢弃就好了。
图像分割
上面这个图片大家一定看过,其实这个图片是有自己的历史的,这个哥们叫Lenna,这个图片是世界上第一个jpeg图片,所以后面做jpeg图片的处理的时候,这个图片就起到demo的作用。
从上图能够看出来,左边的图片是原始图片,而右边是分割以后的图片,分割的过程就是将图像被分割成大小为8X8的小块,好的 第一步已经结束了。
颜色空间转换
所谓的颜色空间转换就是指我们将RGB类别的图片转化为YCbCr类型的图,所谓RGB的图片就是我们认知图片,有三个通道(RED GREEN BLUE),通过不同颜色的混合来呈现不同的颜色.而所谓的颜色空间就是一种颜色的表达方式,例如刚刚说的RGB就是一种颜色空间。
到这里咱们来放大一个小块,看看如何压缩的。
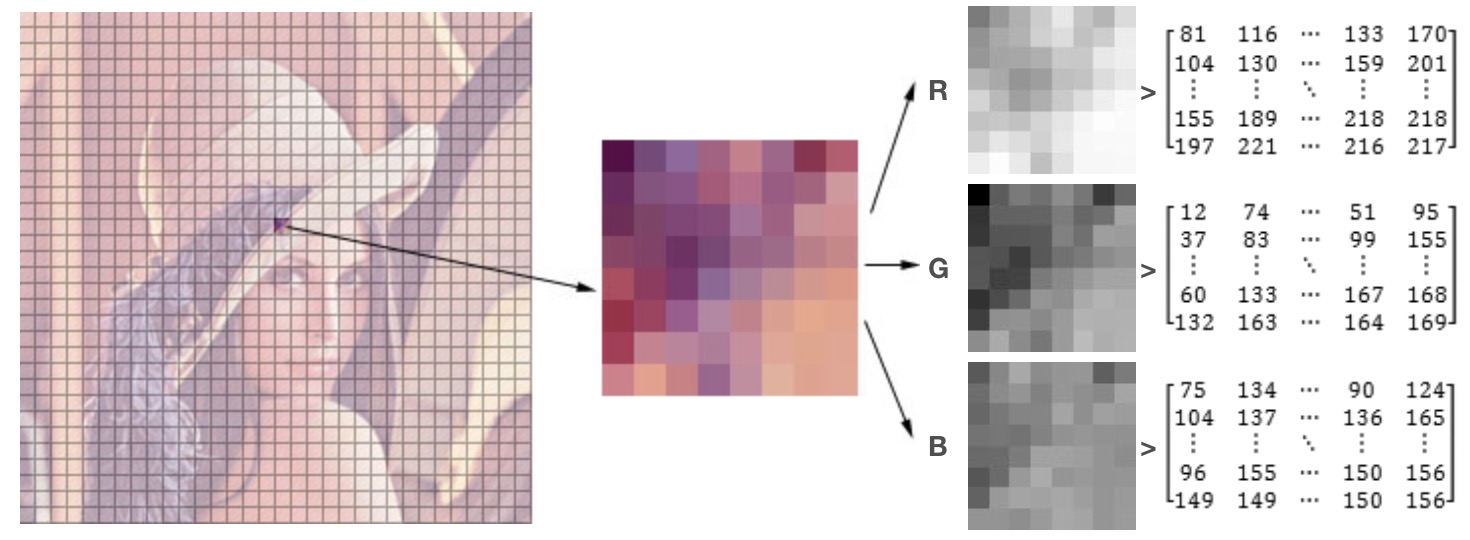
上图看起来就是比较轻松了,其中一个小块分成RGB三个通道,然后再放大就是一个矩阵,且矩阵的取值范围为[0,255].
不同的颜色模型各有不同的应用场景,例如RGB模型适合于像显示器这样的自发光图案,而在印刷行业,使用油墨打印,图案的颜色是通过在反射光线时产生的,通常使用CMYK模型,而在JPEG压缩算法中,需要把图案转换成为YCbCr模型,这里的Y表示亮度(Luminance),Cb和Cr分别表示绿色和红色的“色差值”。
上面提到色差的名词,你可能会觉得这个又是什么东西呢?其实我们知道最早的电视是黑白电视,也就是不同的东西通过亮度来表示,记得那个时候一到黑头的场景就是啥也看不到了,后来彩色电视机出现以后,需要通过添加两个通道来表示颜色,所以人们在Y信号之外增加了两条色差信号以传输颜色信息,这么做的目的是为了兼容黑白电视机,因为黑白电视只需要处理信号中的Y信号即可。
根据三基色原理,人们发现红绿蓝三种颜色所贡献的亮度是不同的,绿色的“亮度”最大,蓝色最暗,设红色所贡献的亮度的份额为KR,蓝色贡献的份额为KB,那么亮度用以下公式计算,至于KR和KB就应该算是超参数了。
Y=KR∗R+(1−KR−KB)∗G+KBB
其中KR=0.299 和KB=0.114
而蓝色和红色的色差的定义如下
Cb=2∗(1−KB)B−Y
Cr=2∗(1−KR)R−Y
这样我们就知道通过Y来计算Cb和Cr了。
下面我们来张图让你回忆一下电视机的输出

这是有道理的,还记得我们在文章开始时提到的有损压缩的基本原理吗?有损压缩首先要做的事情就是“把重要的信息和不重要的信息分开”,YCbCr恰好能做到这一点。对于人眼来说,图像中明暗的变化更容易被感知到,这是由于人眼的构造引起的。视网膜上有两种感光细胞,能够感知亮度变化的视杆细胞,以及能够感知颜色的视锥细胞,由于视杆细胞在数量上远大于视锥细胞,所以我们更容易感知到明暗细节
离散余弦变换
这里我们到了其中一个算法部分,任何周期性的函数,都可以分解为为一系列的三角函数的组合,这是傅立叶提出来的,虽然但是没有被立即发表,后来被大家广泛用到信号处理中。我们来看下面这个图。
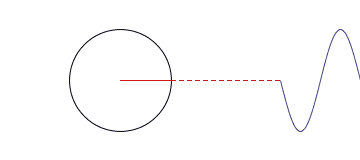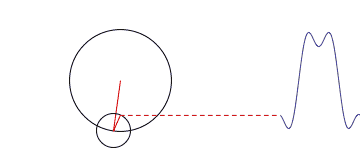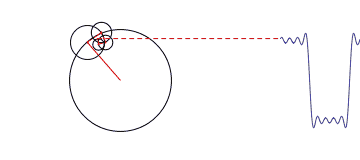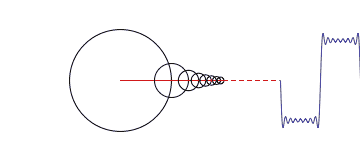
当我们要处理的不再是函数,而是一堆离散的数据时,并且这些数据是对称的话,那么傅里叶变化出来的函数只含有余弦项,这种变换称为离散余弦变换。假设我们有个序列[x0,x1,,,xn],那么可以通过DCT变换得到n个变换级数Fi
Fm=∑xkcos[nπm(21+k)]
而这个变换的逆变换为还原原始数据,所以这一步不是一个有损压缩。
我们有一个长度为8的数字,内容为50,55,67,80,-10,-5,20,30,经过DCT转换压缩过程就如下图。
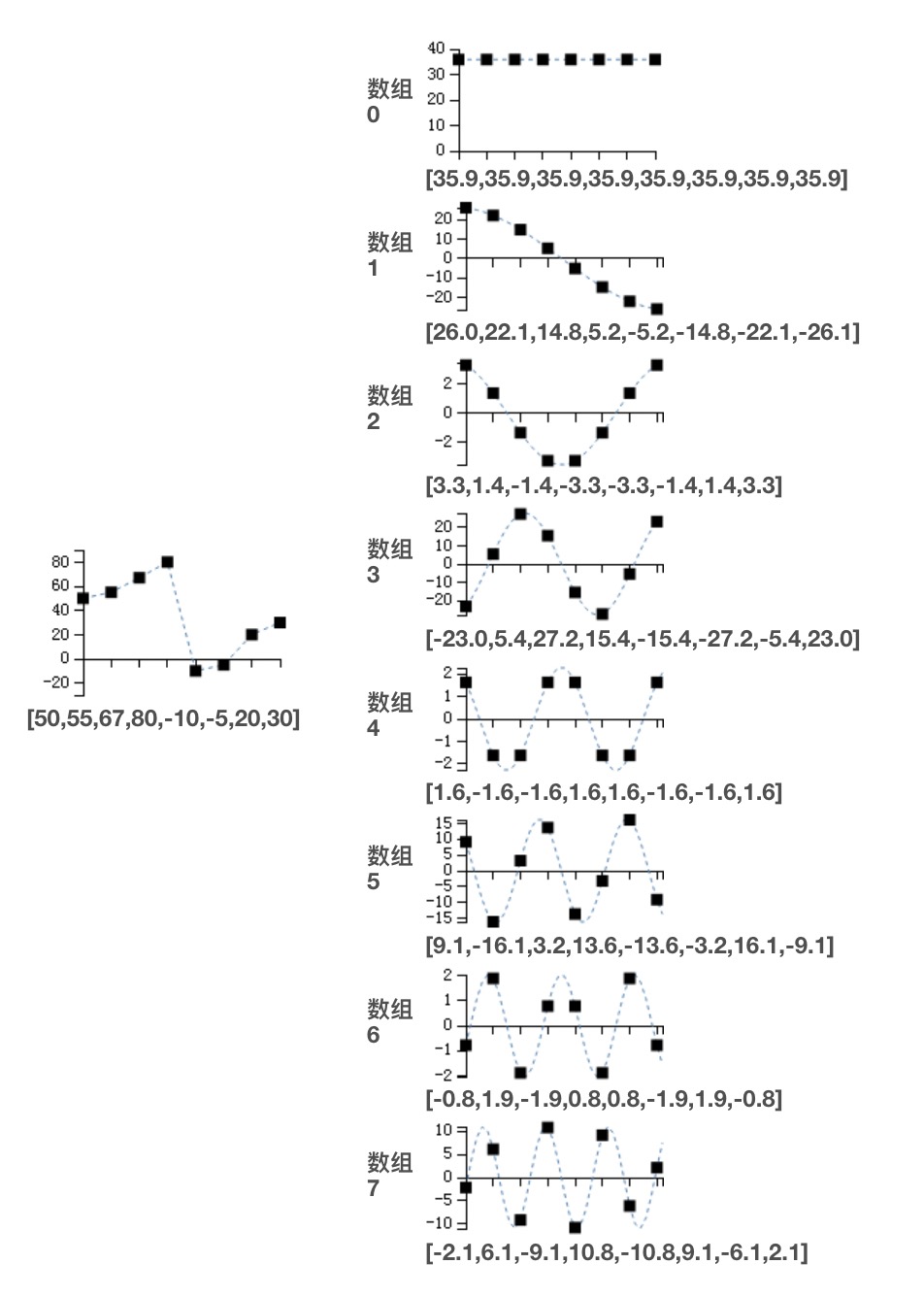
奥妙之处在于,经过DCT,数据中隐藏的规律被发掘了出来,杂乱的数据被转换成几个工整变化的数据。DCT转换后的数组中第一个是一个直线数据,因此又被称为“直流数据”,简称DC,后面的数据被称为“交流数据”,简称AC,这个称呼起源于信号分析中的术语。
在JPEG压缩过程中,经过颜色空间的转换,每一个8X8的图像块,在数据上表现为3个8X8的矩阵,紧接着我们对这三个矩阵做一个二维的DCT转换,二维的DCT转换公式为
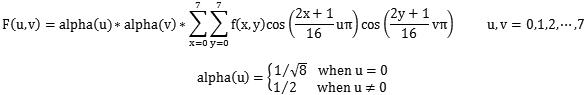
DCT对于一个实际例子,到底能起到什么样的作用呢?
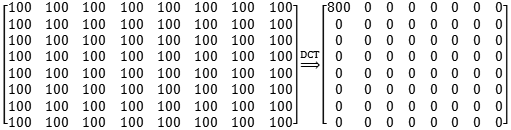
可以看出将一个数字一样的矩阵转变成除了第一个元素有值,但是其他都为0的一个矩阵,其实相当于图片中你看到一个增强的点就够了,其他的都不需要了。也就是我们压缩的对象。
在实际的JPEG压缩过程中,由于图像本身的连贯性,一个8X8的图像中的数值一般不会出现大的跳跃,经过DCT转换会有类似的效果,左上角的直流分量保存了一个大的数值,其他分量都接近于0,我们以Lenna左上角第一块图像的Y分量为例,经过变换的矩阵为

可以看到,数据经过DCT变化后,被明显分成了直流分量和交流分量两部分,为后面的进一步压缩起到了充分的铺垫作用,可以说是整个JPEG中最重要的一步。
数据量化
我们还是从一个例子说起,假如我们有以下一个亮度数据矩阵。
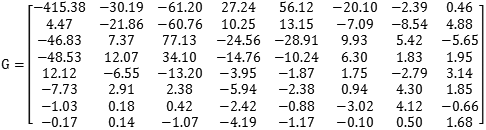
G是我们需要处理的图像矩阵,Q称作量化系数矩阵(Quantization matrices),JPEG算法提供了两张标准的量化系数矩阵,分别用于处理亮度数据Y和色差数据Cr以及Cb。
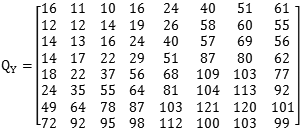
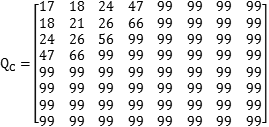
上面两个表是固定的,那么下面我们来看看如何来计算新的亮度矩阵,

round(16−415.38)=−26
这个就是经过第一个量化的过程-26的计算方式,其他以此类推就好。
可以看到,一大部分数据变成了0,这非常有利于后面的压缩存储。这两张神奇的量化表也是有讲究的,还记得我们在第一节中所讲的有损压缩的基本原理吗,有损压缩就是把数据中重要的数据和不重要的数据分开,然后分别处理。DCT系数矩阵中的不同位置的值代表了图像数据中不同频率的分量,这两张表中的数据时人们根据人眼对不不同频率的敏感程度的差别所积累下的经验制定的,一般来说人眼对于低频的分量必高频分量更加敏感,所以两张量化系数矩阵左上角的数值明显小于右下角区域。在实际的压缩过程中,还可以根据需要在这些系数的基础上再乘以一个系数,以使更多或更少的数据变成0,我们平时使用的图像处理软件在生成jpg文件时,在控制压缩质量的时候,就是控制的这个系数,就是我前问提到的,压缩质量默认是75。
矩阵的量化还有最后一步要做,就是把量化后的二维矩阵转变成一个一维数组,以方便后面的霍夫曼压缩,但在做这个顺序转换时,需要按照一个特定的取值顺序。那就看看下面这个图就知道了,非常简单。
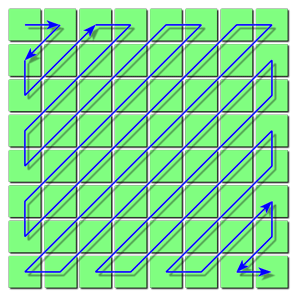
这么做的目的只有一个,就是尽可能把0放在一起,由于0大部分集中在右下角,所以才去这种由左上角到右下角的顺序,经过这种顺序变换,最终矩阵变成一个整数数组
霍夫曼压缩
这个已经是jpeg压缩的最后一步了,其实不管提到什么样样子的压缩算法,我们都是将相同元素出现的连续出现的频次压缩成val->freq的样式,例如000000000->09,表示0出现了9次。
下面我们来看看这样的压缩过程,其中(0,35)表示35前面出现0的次数是0,然后是35,可以看出来压缩的程度还是比较明显的。