决策树算法是一个比较简单的树模型算法,使用熵的概念构建一颗可以做决策的树,比较有意思
决策树是一个贪心算法,在特征空间内进行递归的二分分割。决策树由节点和边组成,内部节点是一个特征,叶子节点表示一个分类。
实际上决策树表示的是在给定特征空间中,类别的一个条件概率。
决策树的3个步骤
1.特征选择
2.决策树生成
3.决策树剪枝
假定训练集D={(x1,y1),(x2,y2)...(xn,yn)} 其中xi=(x1,x2,x3,x4) 为输入实例,n为特征个数,y∈[1,2,3,..,K]为类标签。
构建决策树的损失目标函数通常是正则化的极大似然函数。
熵
提到决策树就不得不说到熵的概念,对于离散变量X的概率分布表示为
P(X=x)=pi
那么随机变量X的熵表示为:
H(X)=−∑pilogpi
并且定义0log0=0
当随机变量X只取两个值时,X的分布为:
P(X=1)=p
P(X=0)=1−p
此时的熵为:
H(p)=−plogp−(1−p)log(1−p)
从上面的公式能够看出:
p=1或是p=0的时候,熵最小,也就是不确定性最小
当p=0.5的时候不确定性最大。
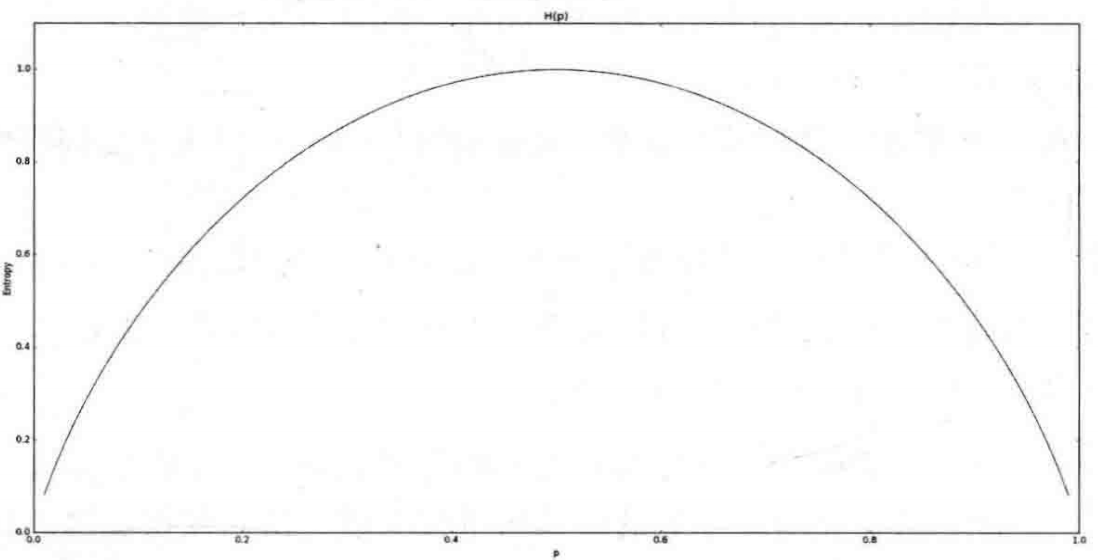
上图表示就是熵的分布。
对于数据D,我们用H(Y)来刻画数据D的不确定程度,当数据D中所有的样本都数据同一类别的时候,则H(Y)=0,那么H(Y)=H(D).给定特征A和训练集D,定义信息增益为g(D, A)=H(D)-H(D|A).
信息增益就是刻画样本由D特征转移A特征的不确定性的减少程度。
ID3树
ID3树的生成过程如下
输入:训练集D、特征集A、特征信息增益阈值α
- 若是训练集合均属于统一分类,则T为单点树,且分类就是样本D的类别。
- 如果A是空集合,则T是空树
- 否则计算g(D,Ai),其中Ai∈A,选择信息增益最大的特征Ag
- 判断Ag的信息增益,如果g(D, Ag)<α,则T为单点树,如果g(D, Ag)>α,则对Ag=ai将D划分为若干个子集Di,且将Di数量最大的作为节点的标记。
- 对第i个子节点,以Di为训练集,以A-{Ag}为特征集合,递归的执行前面的步骤。
CS4.5
CS4.5的树的构建方法和ID3的构建方法几乎相同,唯一的不同就是使用信息增益比来作为关键衡量。
CS4.5的优点如下:
-
使用信息增益率来选择属性,克服信息增益选择属性时候偏向选取值多的不足。
-
树构建的过程中进行剪枝
-
能够完成离散属性离散化的操作。
-
对不完整数据进行处理。
CS4.5仅仅适合数据量在内存级别的计算。
剪枝
不管是cs4.5还是ID3都是数的生成算法而已,但是需要对现实预测更加准确,更需要其他的策略辅助。和大部分数据挖掘算法一样,决策树算法也存在过拟合的问题,而决策树算法解决过拟合的为就是剪枝。决策数剪枝的目的就是提高算法的泛华能力
剪枝流程
假设我们有树T,且T的叶子节点个数为Tf,为树的叶子节点,且每个节点有Nt个样本点,其中属于ck类样本点有Ntk,则有∑Ntk=Nt
令H(t)为叶子节点上t上的经验熵,α>0为参数,则决策树T的损失函数定义为:
C(T)=−∑NtNtklogNtNtk
令
C(T)=∑NtH(t)=−∑∑NtNtklogNtNtk
则C(T)′=C(T)+α∣Tf∣,其中α∣Tf∣为正则项,C(T)
- C(T)=0就意味着Ntk=Nt,即每个节点都是纯的。
- 决策树划分的越细致,则叶子节点T就越多,Tf就越大
- 参数α是控制模型误差和模型复杂度的一个参数。α越大就是选择简单的模型,α=0只是考虑训练数据与模型的拟合程度,不考虑复杂度。
算法描述
- 计算每个叶子节点的经验熵
- 递归的从叶子节点向上回退
- 递归执行以上步骤。
CART树
假设有K个分类,样本点属于第k个分类的概率为pk=P(Y=ck),定义概率分布的基尼指数为:
Gini(p)=∑pk(1−pk)=1−∑pk2
对于样本集合D,属于类别ck样本子集Ck,则基尼指数为:
Gini(D)=1−∑∣DCk∣2
给定特征A,根据是否取某一个值a,样本集合被分为两个集合D1和D2,其中定义基尼指数Gini(D, A):
Gini(D,A)=DD1Gini(D1)+DD2Gini(D2)
以上就表示在特征A的条件下,集合D的基尼指数。
对于简单的二项式分布而言,基尼指数和熵的效果一样,也是度量事件的不确定性。
算法描述
- 对于样本中每个特征A,以及它的每个可能值a, 计算Gini(D, A)
- 选取最优的特征和切分点。
- 递归的切分数据集
CART树的停止条件:
- 样本中节点小于指定值
- 样本中基尼指数小于指定值
- 没有更多特征
CART 连续值和缺失值
连续值处理
假设给定数据集合D和连续特征A,按照从小到大排序,选取M-1个分割点。依次是
2a1+a2,然后按照离散的方式处理。
缺失数据
这个各种学习方式比较头疼的地方。下面来看看缺失值得处理方式。
给定训练集D和特征A,令D~表示D中的特征中没有缺失的样本子集。假定特征A中有M个可能值a1,a2,...am,令D~i表示D~中特征A上取值ai的样本子集,D~k表示D~中属于第k类的样本子集,则有:
D~=⋃Dk~=⋃D~i
假设我们为每个x设定一个权重wx,则
ρ=∑x∈Dwx∑x∈D~wxρk~=∑x∈D~wx∑x∈Dk~wxri~=∑x∈D~wx∑x∈Di~wx
其物理意义为:
ρ:无缺失值占总体的比例
ρ~k:无缺失值样本中,第k类所占比例
r~i:无缺失样本中,在特征A上取值ai样本所占比例。
于是我们可以将信息熵的公式修正为:
g(D,A)=ρ∗g(D~,A)=ρ∗[H(D~)−i=1∑Mri~H(Di~)]
其中H(D~i)=∑ρ~klogρ~k
从而通过划分特征A,让它以不同的概率分散到不同的节点中。
决策树总结
读到这里我们需要明白一个问题,对于决策树算法来说,他是一个分段线性划分,归根结底是具有一定的非线性问题的解决能力的,但是如果特征向量纬度过高会造成纬度灾难(特别是高维度稀疏).所以在决策树算法中,特征选择是非常重要的.
这里还有一个小知识点,树模型适合处理线性问题吗?其实很好理解,树模型这种在空间内画段的算法,不太适合解决线性问题的。典型的问题就如下问题。