贝叶斯分类器

贝叶斯分类器的特点

1. 属性可以离散可以连续
2. 数学基础扎实，分类效率稳定
3. 对缺失值和噪声不敏感
4. 属性如果不相关（独立），效果很好，如果相关效果不低于决策树。

原理

设样本$\vec{x}=x_1,x_2...x_n$， 标记$y \in Y={ c_1, c_2,...,c_k}$,P(X, Y)是X，Y的组合概率分布。训练集合$T={(\vec{x_1},y_1),(\vec{x_2},y_2),..,(\vec{x_n},y_n)} \}$，朴素贝叶斯就是学习联合概率分布P(X, Y),也就是学习如下概率：

先验概率分布:

$$P(Y=c_k), k= 1,2,3,4..K$$

条件概率分布:

$$P(X=\vec{x}|Y=c_k)$$

根据贝叶斯法则，如果分类是确定的，那么用于分类的特征就是独立的。

$$P(x=\vec{x}|Y)=P(X^1=x^1....X^n=x^n|Y=c_k)=\prod P(X^j=x^j|Y=c_k)$$

根据贝叶斯定理：

$$P(Y=c_k|X=\vec{x})=\frac{P(X=\vec{x}|Y=c_k)P(Y=c_k)}{\sum P(X=\vec{x}|y=c_j)P(Y=c_j)}$$

将上面两个公式进行融合：

$$P(Y=c_k|X=\vec{x})=\frac{\prod P(X^{i}=x^{i}|Y=c_k)P(Y=c_k)}{\sum P(X=\vec{x}|y=c_j)P(Y=c_j)}$$

于是贝叶斯分类器可以表示为；

$$y=f(\vec{x})=arg\ max \frac{\prod P(X^{i}=x^{i}|Y=c_k)P(Y=c_k)}{\sum P(X=\vec{x}|y=c_j)P(Y=c_j)}$$

对于同一个分类问题而言，每个分类的计算方式上，分母都是一致的：

$$y=f(\vec{x})=arg\ max \prod P(X^{i}=x^{i}|Y=c_k)P(Y=c_k)$$

现在我们可以抛一个问题出来，对于特征是离散属性，我们可以通过统计获得其概率，如果是连续属性我们应该怎么办呢？

这个时候我们假设在第c类样本中的连续属性符合正态分布，这样带入正态分布方程就能得到取这个连续特征的期望。其中 正态分布的均值和方差都是c类样本中的均值方差的统计值。

还有一个关键点就是如果预测的时候出现一个类别没有和某个类同时出现过,就会出现其中一个先验概率为0,这个时候需要使用拉普拉斯修正

算法描述

看完贝叶斯算法的原理，就很好做算法的实现，对于一个分类问题，需要计算先验概率，再计算条件概率。

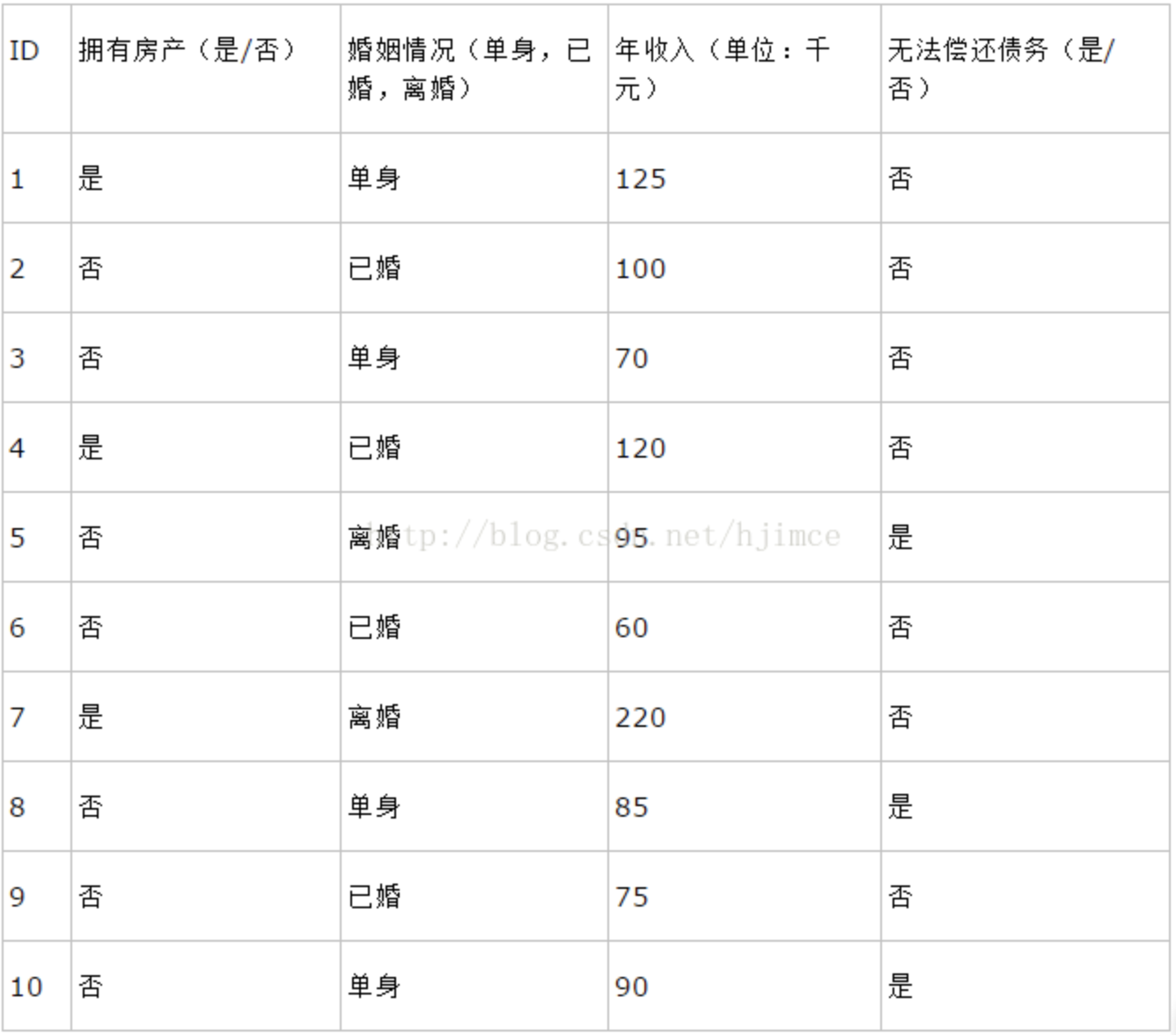
用上表作为原始数据计算
未偿还债务的概率$P(C0)=7/10 $ ，偿还债务的概率为$P(C1)=3/10$。
在未偿还债务的情况下，拥有房产的概率为：$P(x1|C0)=3/7$。同样我们也可以计算未法偿还债务的情况下，已婚的概率为：$P(x2|C0)=4/7$。最后我们就可以求得：

$$P(X|C0)P(C0)=P(x1|C0)P(x2|C0)P(C0)=0.7(3/7)(4/7)$$

同样的我们也可以求得$P(X|C1)*P(C1)$，最后比较一下大小，得到最大的概率类，这个算法就结束了。这个算法原理简单易懂，故称为“朴素”，真是够朴素的。