分类模型的评估
错误率
错误率指的的是分类错误的样本数占总样本的比例
精度
精度指的是分类正确的样本数占总样本的比例。
查准率和查全率
错误率和精度虽然常用,但是对于某些问题来说并不能完全的评估一个模型好坏。下面来看一个混淆矩阵然后来说明我们我概念。
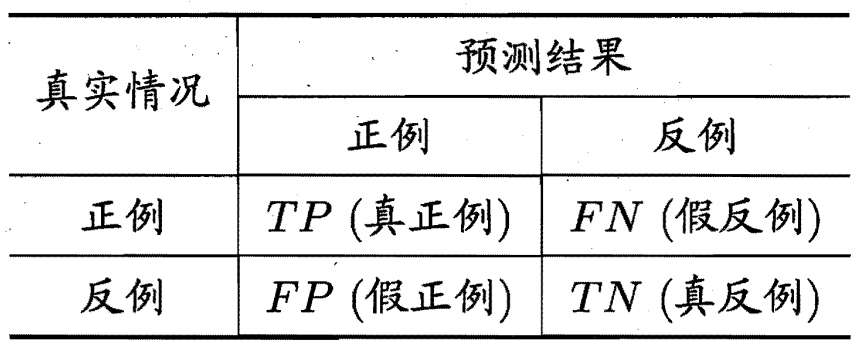
查准率的定义为:
P=TP+FPTP
查全率为:
R=TP+FNTP
当一个数据处理完成时,排在上面的是被认为是最可能的正样本,排在下面的是认为是最不可能正样本。
当我们寻找不同的阈值作为区分正样本和负样本的时候就能画出P-R曲线。
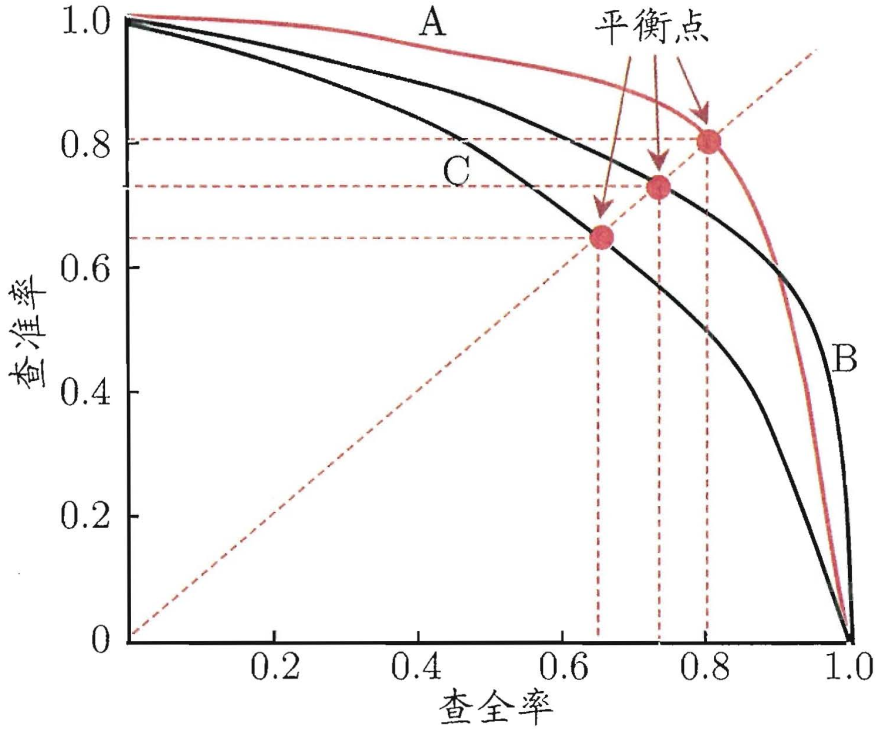
如果一个模型的P-R曲线被另一个模型的P-R曲线包住,那么就能够知道第一个模型劣与第二个模型。
上图中的平衡点,就是查全率和查准率相等是的取值。
F1度量:
样本总数:D
F1=D−TP−TN2TP
F1度量的一般形式:
F=α2P+R(1+α2)×P×R
α=1的时候退化为普通的F度量,α>1查全率影响更大,α<1查准率更重要。
ROC 和 AUC
ROC 全称是"受试者工作特征" (Receiver Operating Characteristic) 曲线,与 P-R 曲线使用查准率、查全率为纵、横轴不同, ROC 曲线的纵轴是"真正例率" (True Positive Rate,简称 TPR),横轴是"假正例率" (False PositiveRate,简称 FPR) 。
TPR=TP+FNTP
FPR=TN+FPFP
若一个学习器的 ROC 曲线被另一个学习器的曲线完全"包住", 则可断言后者的性能优于前者;若两个学习器的 ROC 曲线发生交叉,则难以-般性地断言两者孰优孰劣 . 此时如果一定要进行比较, 则较为合理的判据是 比较 ROC 曲线下 的面积,即 AUC (Area UnderROC Curve)
P-R曲线和ROC曲线有什么区别呢?
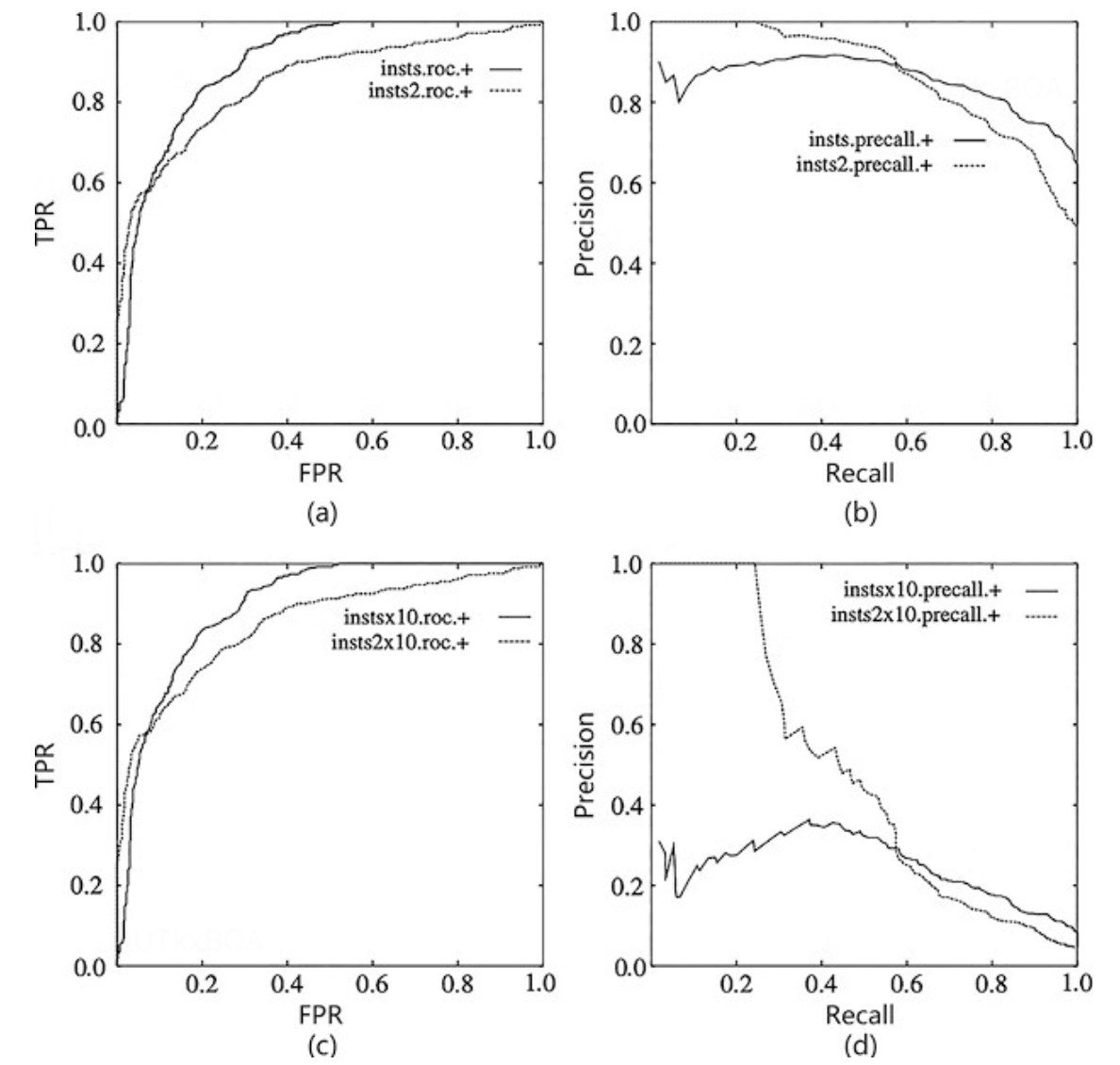
ROC曲线当正负样本分布发生变化时,ROC形状几乎不变,但是P-R曲线变化剧烈.如上图的(a)和©的ROC,当负样本增加为原来的10倍,两个数据集的ROC没有变化,因为ROC的纵坐标是TPR,横坐标是FPR,计算比值的时候,TPR几乎不会发生变化,因为正样本没有变,但是对于FPR来说,负样本增加直接导致的分母的变大,这个时候错分的正样本的负样本也会增加,但是幅度一定不会比分母大,整体来看TPR和FPR会稍微减小,但是ROC变化不大,所以ROC可以避免正负样本不均带来的干扰,能有效的评估模型本身的效果。
但是对于PR曲线就如上图的(b)和(d),可以看到当负样本增加了原来的10倍,召回率不变的情况下,模型一定会找回更多的负样本,所以精确率会下降,因为PR曲线对样本分布比较敏感,不适合作为模型的整体评估工具。这里PR曲线也不是一无是处的,在异常检测场景,一般对正样本的关注点比较高,使用PR曲线也是一个不错的选择。
当然研究者如果关心模型在特定数据集上的表现,会使用P-R曲线来评估.
从物理的角度讲,AUC是ROC曲线下的面积,这个这地球人都知道的,如果从概率的角度理解,AUC是什么样的概念呢?其实AUC考虑的是样本排序的质量,它与排序误差紧密相关。从概率角度看AUC有另一种表达。
AUC=∣P∣×∣N∣∑i∈Pranki−2∣P∣×(∣P∣+1)
rank为样本排序有关,从1开始,|P|是正样本数,|N|为负样本数。所以AUC计算主要与排序相关,对排序敏感,对预测的实际值并不敏感。
下面举一个例子,来看看上面公式如何计算?
| rank |
ture value |
score |
| 4 |
P |
0.8 |
| 3 |
N |
0.6 |
| 2 |
P |
0.5 |
| 1 |
N |
0.3 |
AUC=2∗2(4+2)−22(2+1)=0.75
就是上面的AUC。

对于分子部分的接受可以这么去思考,对于第一个正样本来讲,他与两个负样本的排序组合有两种,(1,00,01),(1,01,00),而对于第二个样本来讲正样本和负样本的组合只有一种,所以最终就是43
auc 等价于随机抽取一个正样本和一个负样本,正样本排在负样本之前的概率。
AUC的数学证明