正则化
正则化是结构风险最小化策略的实现,模型越复杂,正则化项越大(参数越多),所以正则化项可以采用参数向量的范数。正则化的目的是选择经验风险和复杂度同时最小的一个模型。正则化的核心目的是增加部分偏差的情况下减少方差。
正则化选择
我们经常使用L1范数或是L2范数进行作为正则化项,甚至你还知道引入这种范数能够减低过拟合的问题,但是引入了正则化项就能防止过拟合呢?
先看看这些范数都是怎么定义的。ω 是属性权重
L0范数: ω 的非0元素的个数。
L1范数: ω 的值得和
L2范数: ω 的值得平方和。
L1 范数和 L2 范数正则化都有助于降低过拟合风险,但前者还会带来一个额外的好处:它比后者更易于获得"稀疏" (sparse)解,即它求得的 ω 会有更的非零分量.
demo
下面我们通过一个例子来理解:
假设我们的问题有两个特征,那么就有两个权重w1, w2,我们将其作为两个坐标轴.
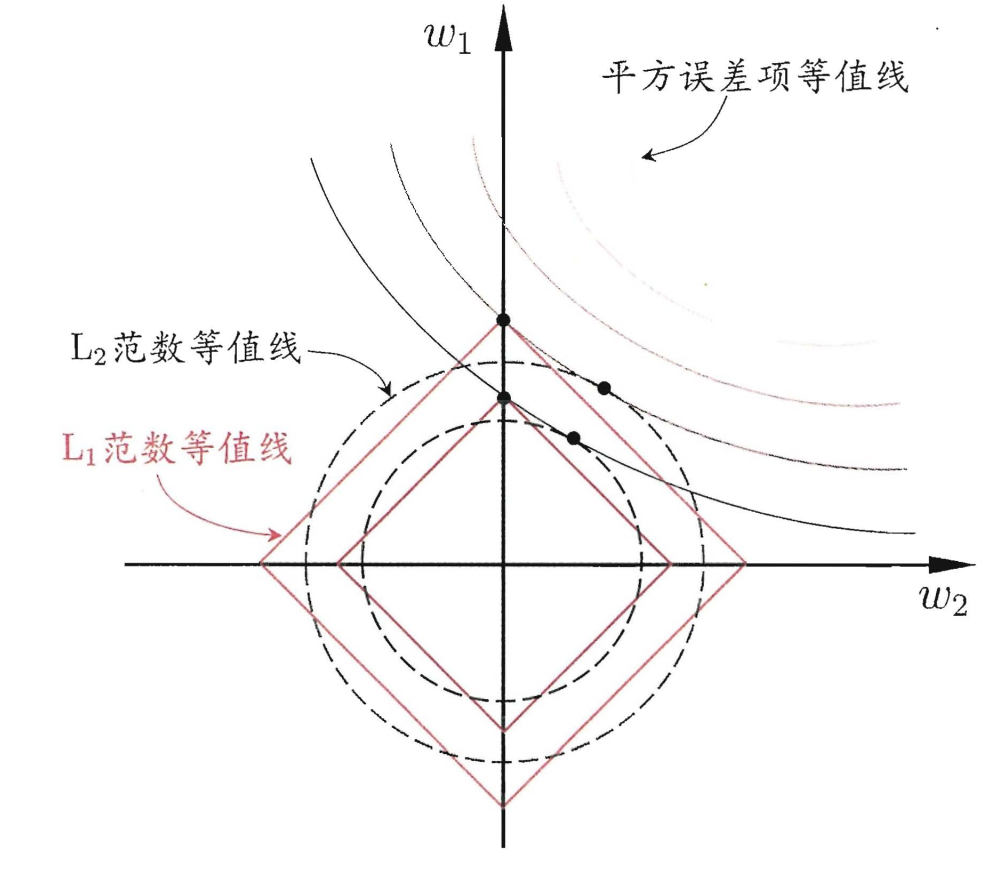
(ω1 ,ω2)空间中平方误差项取值相同的点的连线,再分别绘制出 L1 范数与 L2范数的等值线,即在(ω1 ,ω2)空间中 L1 范数取值相同的点的连线, 以及 L2 范数取值相同的点的连线.从图中能够看出,L1范数是方正的,棱角处更容易出现0值。换种说法,采用 L1 范数时平方误差项等值线与正则化项等值线的交点常出现在坐标轴上 ? 即 ω1 或 ω2 为 0 , 而在采用 L2 范数时,两者的交点常出现在某个象限中,即 ω1 或 ω2 均非 0; 换言之?采用 L1 范数比 L2 范数更易于得到稀疏解.
注意到 ω 取得稀疏解意味着初始的 d 个特征中仅有对应着 ω 的非零分量的特征才会出现在最终模型中 7 于是,求解 L1 范数正则化的结果是得到了仅采用一部分初始特征的模型;换言之,基于 L1 正则化的学习 方法就是一种嵌入式特征选择方法?其特征选择过程与学习器训练过程融为一体, 同时完成.
温馨提示
这里需要说明一下,在神经网络中,所谓的正则化表示的是对每一层的权重做惩罚,而不是对偏置做惩罚。