集成学习

在数据疯狂增长的今天，单个学习器似乎不能满足我们对于数据挖掘的要求，这个时候我们需要讲多个学习器集成使用，从而提高整个学习器的泛华能力。

目前的集成学习方法大致可分为两大类?即个体学习器问存在强依赖关系、必须串行生成的序列化方法?以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是 Boosting，后者的代表是Bagging 和"随机森林" (Random Forest).

Boosting

Boosting 是一族可将弱学习器提升为强学习器的算法.这族算法的工作机制类似:先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器;如此重复进行，直至基学习器数目达到事先指定的值 T ， 最终将这 T 个基学习器进行加权结合.Boosting 族算法最著名的代表是 AdaBoost。

Boosting算法要涉及到两个部分，加法模型和前向分步算法。加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下：

$$F(x;p)=\sum\beta h(x;a)$$

h(x;a)代表一个弱分类器，a是分类器的参数，$\beta$是这个分类器在全部分类器的占比。

AdaBoost

现在通过一个demo来说明算法:

原始数据:

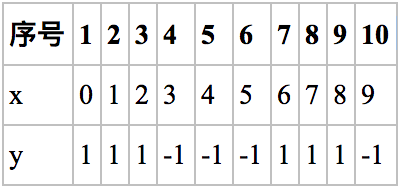
对于上面一组数据，我们需要构建强分类器对其进行分类。x是特征，y是标签。

令权值分布 $D={w_1, w_2,...,w_n}$

并假设一开始的权值分布是均匀分布，则w=0.1

我们发现阈值取2.5时分类误差率最低，得到弱分类器为：

1. 根据第一个弱分类器发现"6,7,8"被错分，错误率e=0.3
2. 计算H1权重，$\alpha=\frac{1}{2}log\frac{1-e}{e}=0.4236$
3. 更新训练样本数据的权值分布，用于下一轮迭代，对于正确分类的训练样本“1 2 3 4 5 9 10”（共7个）的权值更新为：然后计算G(x)在分类器中的系数，然后更新新的权重分布，

$$w=\frac{w_1}{z_1} exp(-\alpha y G(x))$$

其中z是归一化常数$z=2\sqrt{e(1-e)}$

得到新的权值分布，从各0.1变成了:

$$D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)$$

可以看出，被分类正确的样本权值减小了，被错误分类的样本权值提高了。

的到的强分类器为:

$$sign(F(x))=sign(0.4236 G(x))$$

4.进行第二轮迭代。H2(x)把样本“3 4 5”分错了，根据D2可知它们的权值为D2(3)=1/14，D2(4)=1/14， D2(5)=1/14，所以H2(x)在训练数据集上的误差率：

$$e_2=\frac{3}{14}$$

根据$e_2$计算$H2$的权重:

$$\alpha=0.6496$$

然后更新权重；

…

$$f2(x)=0.4236H1(x) + 0.6496H2(x)$$

…依次类推就叠加一个集成模型。

原理

现在了解算法的基本流程，那么开始深入了解其中细节问题:

为什么计算$\alpha$的方式是这样的？

我们已经知道AdaBoost是采用指数损失，由此可以得到损失函数：

$$Loss=\sum exp(-y (F_{m-1} + \alpha G(x))$$

因为$F_{m-1}$已知，化简公式；

$$Loss= exp(-y\alpha G(x))w$$

其中 $w=exp(−y(F_{m−1}))$,这个就是每轮迭代的样本权重！依赖于前一轮的迭代重分配。

Bagging

随机森林

随机森林的生成方法：

1.从样本集中通过重采样的方式产生n个样本

2.假设样本特征数目为a，对n个样本选择a中的k个特征，用建立决策树的方式获得最佳分割点

3.重复m次，产生m棵决策树

4.多数投票机制来进行预测

（需要注意的一点是，这里m是指循环的次数，n是指样本的数目，n个样本构成训练的样本集，而m次循环中又会产生m个这样的样本集）

bagging算法比较简单的是每个弱分类器都是一个单独的个体，通过投票、平均法等方法获得最后的分类。