样本不均有很多方式能够解决，那么我们来总结一下都有哪些可以做。

• 从样本侧解决
• 从标签做手脚
• 从损失函数侧向办法

这个文章就是从损失函数的视角解决这个问题，并且会顺便介绍几个好用的损失函数。

样本不均下的损失函数

首先我们还是要从交叉熵的损失函数说起，如公式1.1

$$L=-y log(p)-(1-y)log(1-p) \tag{1.1}$$

p为预测概率，y是真实标签。

\begin{equation} L_{CE} =\left\{ \begin{array}{ll} -log(p) \ \ y=1\\ -log(1-p) \ y=0 \\ \end{array}\right. \end{equation}

样本不平衡

最终的损失函数为

$$L=\frac{1}{N}(\sum^{m}_{y_{i}=1} -log(p) + \sum^{n}_{y_{i}=0} -log(1-p))$$

其中$y_{i}$表示标签， m位正样本数，n表示负样本数。当样本分布失衡时，在损失函数L的分布也会发生倾斜，如m<<n时，负样本就会在损失函数占据主导地位。由于损失函数的倾斜，模型训练过程中会倾向于样本多的类别，造成模型对少样本类别的性能较差。
面对这样的问题，可以使用平衡交叉熵函数的方式， 这个在本站搜索机器学习之采样介绍了这种方法。 今天主要介绍focal loss损失函数。

focal loss

focal loss也是针对样本不均衡问题，从loss角度提供的另外一种解决方法。

\begin{equation} L_{jl} =\left\{ \begin{array}{ll} -(1-p)^{\gamma}log(p) \ \ y=1\\ -p^{\gamma}log(1-p) \ y=0 \\ \end{array}\right. \end{equation}

p反映了与ground truth即类别y的接近程度, focal loss相比交叉熵多了一个modulating factor （调节因子）， $(1-p)^{\gamma}$,对于分类准确的样本p=1, modulating factor就趋近于0，对于分类不准确的样本
$1-p$趋近于1， modulating factor趋近于1，即相比交叉熵损失，focal loss对于分类不准确的样本，损失没有改变，对于分类准确的样本，损失会变小。 整体而言，相当于增加了分类不准确样本在损失函数中的权重。而在样本不均的任务重，小样本经常被当成不容易分类成功的样本进行加权惩罚。

focal loss vs balanced cross entropy

focal loss相比balanced cross entropy而言，二者都是试图解决样本不平衡带来的模型训练问题，后者从样本分布角度对损失函数添加权重因子，前者从样本分类难易程度出发，使loss聚焦于难分样本。所以这两种方式对于解决样本不均的视角是相差很大。 focal loss解决问题的范围应该包含balanced cross entropy解决的问题集合的。

梯度对比

要想使模型训练过程中聚焦难分类样本，仅仅使得Loss倾向于难分类样本还不够，因为训练过程中模型参数更新取决于Loss的梯度。
如果Loss中难分类样本权重较高，但是难分类样本的Loss的梯度为0，难分类样本不会影响模型学习过程。
所以我们来看看 focal loss的梯度示意图。

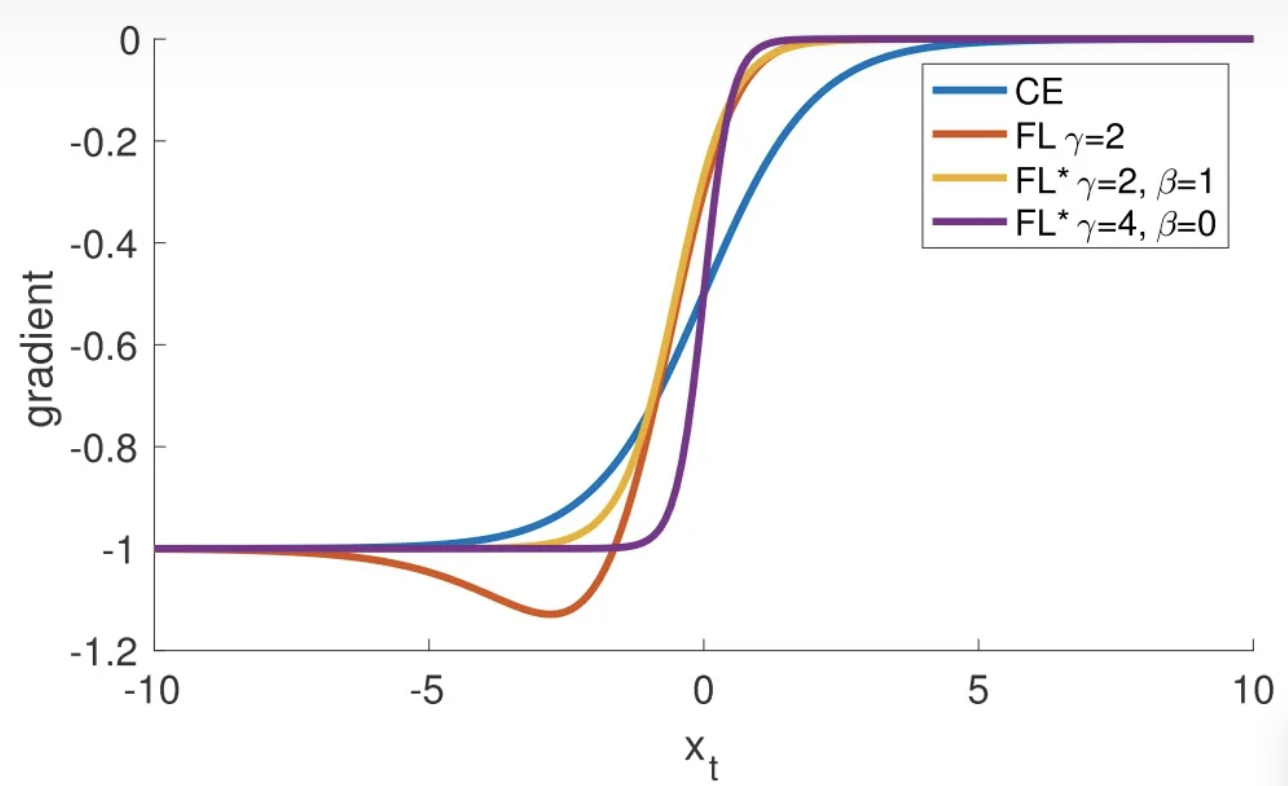
其中$y_{t} \in [-1,1], x_{t}=y *x$。也就是说$x_{t}>0$的部分是预测值为正例子，同样是p>0.5这部分case， 我们可以发现，当预测为正例并且实际是正例的时候，$x_{t}$接近于0， 预测负实际负也是类似。 也就是说当模型预测正确的样本中， 梯度是接近于0的。

$x_{t}>0$表示的预测争取的样本， 正例只是举一个例子。通过上面的图形可以发现，模型目前对正确的样本开始减少关注（容易分对的样本），梯度中占主导的是错误样本(难分样本)。

GHM Loss

Focal Loss 损失函数注重了对 hard example 的学习，但不是所有的 hard example 都值得关注，有一些 hard example 很可能是离群点，这种离群点当然是不应该让模型关注的。
GHM (gradient harmonizing mechanism) 是一种梯度调和机制，GHM Loss 的改进思想有两点：
1）就是在使模型继续保持对 hard example 关注的基础上，使模型不去关注这些离群样本；
2）另外 Focal Loss 中， 的值分别由实验经验得出，而一般情况下超参 是互相影响的，应当共同进行实验得到。
那么咱们就来看看这个GHM 损失函数是怎么来的？
首先定义了一个变量g，叫做梯度模长（gradient norm）：

$$g=|p-p^{*}|$$

其中$p^{*}$是真值，p是预测值。g正比于检测的难易程度，g越大则检测难度越大。
GHM对易分类样本和难分类样本都衰减，那么真正被关注的样本，就是那些不难不易的样本。而抑制的程度，可以根据样本的数量来决定。使用梯度密度GD来定义

$$GD(g)=\frac{1}{l(g)} \sum_{i=1}^{N}\delta(g_k,g)$$

其中

• $GD(g)$是计算在梯度g位置的梯度密度；
• $\delta(g_k,g)$就是样本k的梯度$g_k$是否在$[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]$这个区间内。
• $l(g)$就是$[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]$这个区间的长度，也就是$\epsilon$

因此梯度密度GD(g)的物理含义是：单位梯度模长g部分的样本个数。
接下来就简单了，对于每个样本，把交叉熵CE×该样本梯度密度的倒数即可！

$$L_{CHM}=\sum_{i=1}^{N} \frac{L_{CE(p_{i},p_{i}^{*})}}{GD(g_{i})}$$

$L_{CE}(p_i,p_{i}^{*})$表示第i个样本的交叉熵损失；
$GD(g_i)$表示第i个样本的梯度密度；

反思

上面讲到，由于Loss梯度中，难训练样本起主导作用，即参数的变化主要是朝着优化难训练样本的方向改变。当参数变化后，可能会使原先易训练的样本 发生变化，即可能变为难训练样本。当这种情况发生时，可能会造成模型收敛速度慢，正如文章中提到的那样。为了防止难易样本的频繁变化，应当选取小的学习率。防止学习率过大，造成 变化较大从而引起 的巨大变化，造成难易样本的改变。