排序

讲解使用什么语言作为demo？其实很多人讲解算法都使用的是java或者是C++，因为他们认为算法本身就是性能的质变，所以语言也要用尽可能快的语言（和我原来的思想很像），对于这个问题现在我是这样理解的，算法的核心是思想，你需要明白的也是思想，至于什么语言将来你使用的时候针对你的编程环境使用就好了，学习贵在学会，不要太纠结细节。

这一章节主要讲排序算法，那么我们就先了解各种常用的排序算法的使用场景有哪些？下面这个图片应该是记录比较全面的。

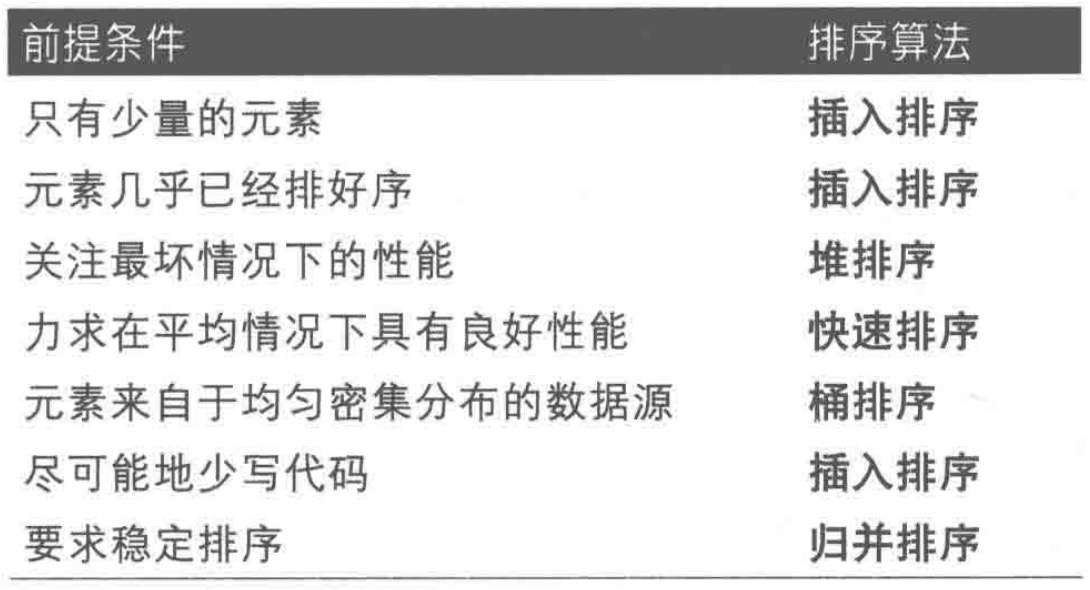
首先我们要定义的标准然后实现的方式来继承。

class Sort(object):
    @abc.abstractmethod
    def sort(self, array_list):
        raise NotImplementedError

插入排序

代码展示

class InsertSort(Sort):

    def insert_sort(self, arr):
        for i in range(1, len(arr)):
            key = arr[i]
            j = i - 1
            while j >= 0 and key < arr[j]:
                arr[j + 1] = arr[j]
                j -= 1
            arr[j + 1] = key
        return arr

    def sort(self, array_list):
        arr = self.insert_sort(array_list)
        return arr

以上是插入排序的python代码，他的大致的思想是不断的往arr这个数组里插入数据，插入的数据也就是代码中的key变量，从后往前插入，如果比当前的元素大，就把当前元素后移，知道找到比key小的就停下来，将元素放到这里。

复杂度分析

然后我们来分下下这个算法的上下限制，最快的时候就是$`$O(n)$`$了，原数组基本有序，遍历一遍不需要做元素的移动，最差的当然就是倒序的了，每次都要移动所有的元素，所以整体的复杂度为$`$O(n^2)$`$,

选择排序

代码展示

class SelectSort(Sort):
    def __select_min_idx(self, arr):
        min = sys.maxint
        min_idx = 0
        for idx in range(len(arr)):
            if arr[idx] < min:
                min = arr[idx]
                min_idx = idx
        return min_idx

    def sort(self, array_list):
        for i in range(len(array_list)):
            idx = self.__select_min_idx(array_list[i:])
            swap(array_list, i, idx + i)
        return array_list

选择排序的思路更加粗暴和简单，我就是每次都转转变成找极值的问题，例如上面的代码，我每次都找最小的元素和当前的遍历元素进行交换，这样我能保证遍历完数组的时候就是整体数组有序的时候。

复杂度分析

选择排序是性能比较差的排序，每次找极值的时候都需要遍历整个元素，所以算法复杂度很好分析，就是$O(n^2)$,并且没得商量，和原始数据是否有效无关。

堆排序

堆

堆是一种非线性结构，（本篇随笔主要分析堆的数组实现）可以把堆看作一个数组，也可以被看作一个完全二叉树，通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组

按照堆的特点可以把堆分为大顶堆和小顶堆

大顶堆：每个结点的值都大于或等于其左右孩子结点的值

小顶堆：每个结点的值都小于或等于其左右孩子结点的值

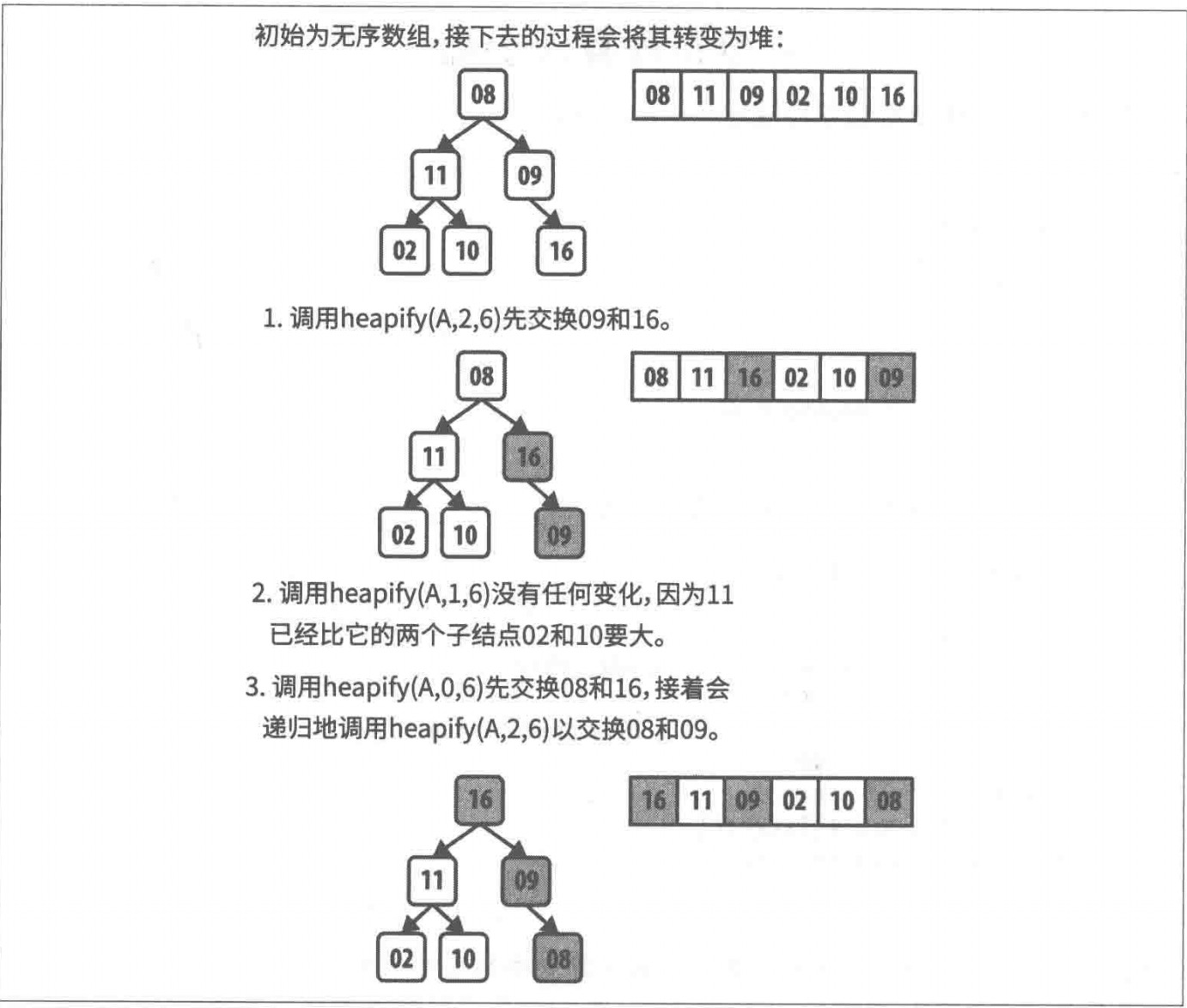
先来看看上面的图片，是堆排序的过程。

class HeapSort(Sort):
    def heapify(self, arr, n, i):
        largest = i
        l = 2 * i + 1
        r = 2 * i + 2
        if l < n and arr[i] < arr[l]:
            largest = l
        else:
            largest = i
        if r < n and arr[largest] < arr[r]:
            largest = r
        if largest != i:
            swap(arr, largest, i)
            self.heapify(arr, n, largest)

    def __build_heap(self, arr):
        n = len(arr)/2 - 1
        for i in range(n, -1, -1):
            self.heapify(arr, n, i)

    def sort(self, array_list):
        self.__build_heap(array_list)
        n = len(array_list)
        for i in range(n - 1, 0, -1):
            swap(array_list, i, 0)
            self.heapify(array_list, i, 0)
        return array_list

以上是堆排序算法的过程，我来看看算法的流程，首先对array_list进行建堆，所谓建立堆就是不允许一个父节点小于他的子节点而已，进行self.heapify操作，对于构建好的堆一直取堆顶的元素也就是sort方法，就称为堆排序，这里涉及到一个递归，就是每次有一个节点调整以后，相应的会不断移动和这个元素相关的元素。这里的核心方法是** heapify**方法，这个方法主要起到的作用是调整堆的机构，大家和把这段代码拿到自己机器上调试，看看每次的运行结果。

复杂度分析

堆排序的核心操作是heapify，在__build_heap的过程中，这个函数会被调用$`$\frac{n}{2}-1$`$次，而实际的排序中，这个方法会被调用n-1次，总共被调用$`$\frac{3n}{2}-2$`$次，堆本质是一个树，树的高度是$`$logn$`$，然后还有一个递归的操作，每次校正从堆底到堆等最多也就是$`$logn$`$，整个过程比较次数不会操作$$2n$$次，所以整体算法的复杂度就是$$O(nlogn)$$

快速排序

class QuickSort(Sort):
    def qsort(self, arr, left, right):
        if left >= right:
            return
        i = left
        j = right
        key = arr[left]
        while i < j:
            while i < j and key <= arr[j]:
                j -= 1
            arr[i] = arr[j]
            while i < j and key > arr[i]:
                i += 1
            arr[j] = arr[i]
        arr[i] = key
        self.qsort(arr, left, i - 1)
        self.qsort(arr, i + 1, right)

    def sort(self, array_list):
        self.qsort(array_list, 0, len(array_list) - 1)
        return array_list

还有一种写法，可能更好理解一些。

def quickSort(arr):
    if len(arr) <= 1:
        return arr
    else:
        smaller = []
        equal = []
        greater = []
        pivot = arr[random.randint(0, len(arr) - 1)]
        for elem in arr:
            if elem < pivot:
                smaller.append(elem)
            elif elem == pivot:
                equal.append(elem)
            else:
                greater.append(elem)
    return quickSort(smaller) + equal + quickSort(greater)

快速排序的思想也比较简单，主要是找到一个基准，让基准左边的元素比基准小，右边的元素比基准大，qsort这个方法就是移动元素来找到咱们说的基准，第一个while循环里想要找到的是比基准小的元素，所以一旦发现比基准大的就直接左移，找到以后就记下这个元素，保存到arr[i]这里， 然后就是从左边找比基准大的元素的了，同理也是按照上文说的方法找，找到以后，就要交换这两个元素(arr[i],arr[j]),然后找到相应的key的位置，就递归的对左边和右边的元素都做这样的操作。

复杂度分析

这是个比较有趣的算法，因为如果数据是逆序的时候，这个算法的复杂度会退化到$`$O(n^2)$`$,当然平均状况下会是$`$O(nlogn)$`$

桶排序

这算法是比较少见的不基于比较的排序算法

class BucketSort(Sort):

    def sort(self, array_list):
        n = max(array_list) + 1
        arr = [0 for i in range(n)]
        for item in array_list:
            arr[item] += 1
        array_list = list()
        for i in range(n):
            while arr[i] != 0:
                array_list.append(i)
                arr[i] -= 1
        return array_list

堆排序算法要求你的数据是范围是确定的，然后申请一个这么大的数组，将元素的下标元素打上标记，虽然这个算法不基于比较，但是是构建到一个有序数组的基础上的。

复杂度分析

能够看出这个算法的最坏复杂度和平均复杂度都是$`$O(n)$`$

归并排序

上文介绍的的基本上都不需要借助于外部存储空间，但是归并算法是需要借助外部空间的。

class MergeSort(Sort):
    def merge(self, arr1, arr2):
        arr = []
        h = j = 0
        while j < len(arr1) and h < len(arr2):
            if arr1[j] < arr2[h]:
                arr.append(arr1[j])
                j += 1
            else:
                arr.append(arr2[h])
                h += 1
        if j == len(arr1):
            for i in arr2[h:]:
                arr.append(i)
        else:
            for i in arr1[j:]:
                arr.append(i)
        return arr

    def sort(self, array_list):
        if len(array_list) <= 1:
            return array_list
        middle = len(array_list) / 2
        left = self.sort(array_list[:middle])
        right = self.sort(array_list[middle:])
        return self.merge(left, right)

上面的代码就是一个完整的归并排序，其中merge方法就是合并两个有序list的操作，在sort方法里，递归的排序数组的一部分，上文说的占用额外的空间就是merge中的数组arr，最后合并最后两个left和right数组就是我们要的有序数组。

算法复杂度

首先确空间复杂度是$`$O(n)$`$,归并排序的归并算法也就是merge算法复杂度是$`$O(n)$`$,然后递归执行这一过程，最后的算法复杂度是$`$O(nlogn)$`$.

不知道大家注意到没有，一个序列中多个归并是完全独立的，这个也就是是说这个算法是比较好完成并行化的，以下可以看下博主这篇文章。