搜索算法
本文会介绍一些常用的搜索算法,搜索在我们实际应用中十分普遍,例如数组查找元素,记事本搜索关键词等等。
查找父类构建
class Search(object):
@abc.abstractmethod
def search(self, arr, key):
raise NotImplementedError
def __init__(self, val ,left, right):
self.val = val
self.left = left
self.right = right
顺序搜索
最简单的搜索但是顺序搜索,给你一个数组,判断一个数字是否存在,怎么做呢?第一想法当然是一个一个看是否是和我要找的数字一样。
class OrderSearch(Search):
def __init__(self):
pass
def search(self, arr, key):
for item in arr:
if item == key:
return item
return -1
简单到令人发指是不是,好的不说了,一切尽在不言中。
复杂度分析
理论上我们最差的复杂度就是重头遍历到最后,如果查找到的复杂度一定是小于等于n的,所以算法的整体复杂度是O(n)
二分查找
二分查找是一种比较好的查找算法,将原始数据利用充分的算法,下面来看代码
class BinSearch(Search):
def search(self, arr, key):
left = 0
right = len(arr)
while left < right:
middle = (left + right) / 2
if key == arr[middle]:
return arr[middle]
elif key > arr[middle]:
left = middle + 1
else:
right = middle -1
return -1
看到上面的代码十分清晰,假设你在有序数据查找,那么你每查找一个元素,你都能过滤掉一部分数据,减少搜索的范围,一定是比顺序搜索好用了,就是排序这个条件是比较苛刻。
复杂度分析
从上面的搜索过程能够看出。算法过程类似于树的搜索。每次判断都减少一半判断的数据,所以这个算法的复杂度是O(logn)
散列搜索
我们通过上面的学习知道,二分查找虽然性能较好,但是前置条件比较苛刻,本节说的搜索方法是比其他的算法性能要好。
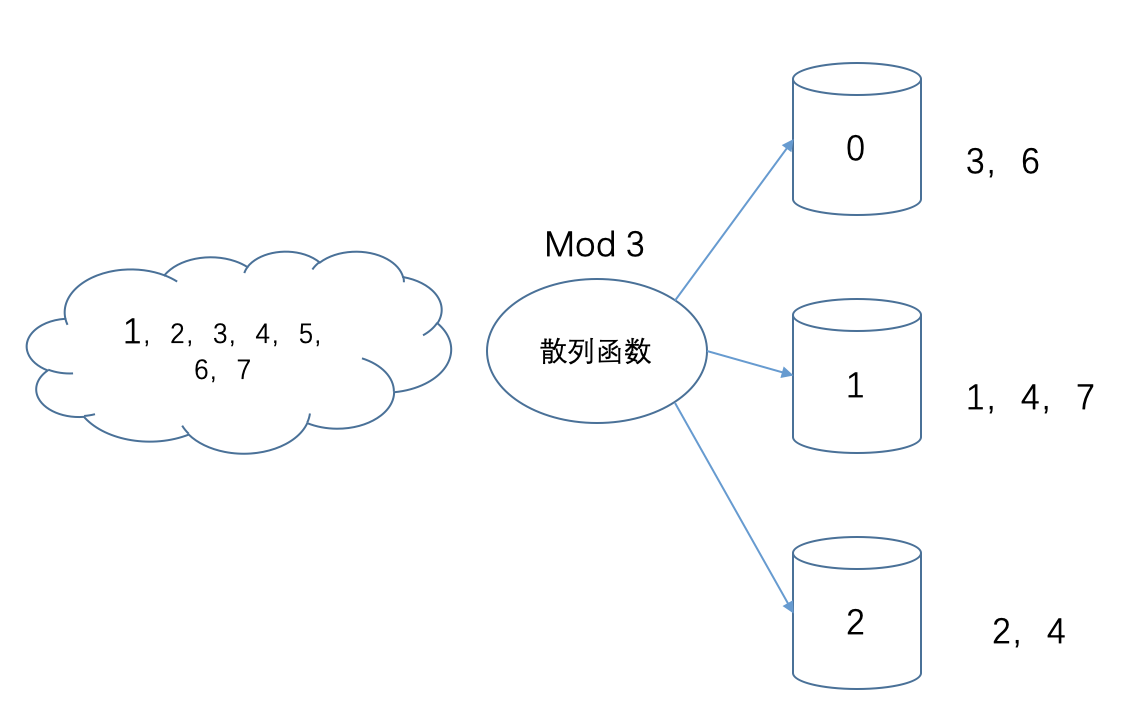
散列搜索的关键点是散列函数,例如我可以取mod以后将mod相同的值放到一个散列表中,然后搜索的时候也进行同样的操作,找到相应的桶,然后在桶内进行顺序搜索。
散列搜索的步骤
- 根据hash函数散列原数据
- 将待查找数据进行同样的hash函数去找相应的桶元素
- 对桶元素进行遍历搜索
从上面的描述我们能够知道,如果hash函数选择的不好,会导致全部元素全部散列到一个桶中,其性能就是扫描所有元素。
class HashSearch(Search):
def __init__(self):
self.mod = 6
def __load_hash_table(self, arr):
hash_dict = dict()
for a in arr:
if hash_dict.get(a % self.mod) is None:
hash_dict[a % self.mod] = [a]
else:
hash_dict[a % self.mod].append(a)
return hash_dict
def search(self, arr, key):
hash_dict = self.__load_hash_table(arr)
m = key % self.mod
if hash_dict.get(m) is None:
return -1
else:
for item in hash_dict.get(m):
if item == key:
return item
return -1
整体代码的散列方式就是从6取模,然后到相应的桶内查找元素即可。需要注意的是,咱们加载散列表这一步如果是工程实现上,仅仅加载一次就可以,放到内存从搜索即可。
复杂度分析
如果散列函数选的好的话,散列表搜索能够完成O(1)的复杂度。
布隆过滤器
对于上面介绍的散列表查找是比较好的算法,但是它也有一个问题就是内存,如果内存空间一定,不断增加元素就势必会造成查找性能下降,本节介绍的算法能够从一定程度上解决这个问题。但是这个算法也有自己的问题,就是它不能保证100%正确。
本质上布隆过滤器是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。
class BloomSearch(Search):
def __init__(self):
self.size = 50
self.bit = 0
self.hash_funs = [lambda e, size: hash(e) % size]
def __add(self, value):
for hf in self.hash_funs:
self.bit |= 1 << hf(value, self.size)
def search(self, arr, key):
for a in arr:
self.__add(a)
for hf in self.hash_funs:
if self.bit & 1 << hf(key, self.size) == 0:
return -1
return key
将原数组进行hash编码然后映射到到bit数组中,bloom之所以不准就是因为如果bit数组不够大,那么很多不同元素会hash出相同的bit编码,所以是可能存在。
还有一个点不知道你能不能观察到,bloom搜索能够进行删除操作吗,当然是不能的,因为这个编码仅仅是位移,单纯删除某一位是没有删除效果的,而且还有可能很多元素编码相同,造成误删除。
复杂度分析
可以看到搜索的效率仅仅和bit的位数有关。所以即是‘O(k)‘,可就是bit的位数,是一个常数时间的算法
二叉搜索树
先看构建的代码
class TreeSearch(Search):
def __build_tree(self, arr):
root = TreeNode(val=arr[0])
for idx, a in enumerate(arr):
head = root
if idx == 0:
continue
node = TreeNode(val=a)
while head is not None:
if head.val > node.val:
if head.left is None:
head.left = node
break
else:
head = head.left
else:
if head.right is None:
head.right = node
break
else:
head = head.right
return root
def search(self, arr, key):
root = self.__build_tree(arr)
while root is not None:
if root.val == key:
return root.val
elif root.val > key:
root = root.left
else:
root = root.right
return -1
上面这个方法写的非常透彻,没有用递归,就是用最朴素的方法构建一个二叉搜索树,思路就是比当前节点小的放到左边节点中,比当前节点大的放到右边节点中。
复杂度分析
对于树的搜索的复杂度就是‘O(logn)‘,也就是树高,但是你实现的时候有没有发现,如果你使用一个有序数组构建这样一棵树的时候就会发现,节点全在一边,并且搜索的复杂度是‘O(n)‘,这个也是搜索树的问题,后面我们会介绍一个种优化这样情况的方法。
局部有序数组搜索
顾名思义,就是数组中局部是有序的,这样的情况能不能使用复杂度更低的算法搜索。例如这样的数组,nums = [4,5,6,7,0,1,2]
class Solution(object):
def search(self, nums, target):
start = 0
end = len(nums) - 1
while start <= end:
middle = (start + end) // 2
start_val = nums[start]
end_val = nums[end]
mid_val = nums[middle]
if mid_val == target:
return middle
if mid_val < end_val:
if mid_val < target <= end_val:
start = middle + 1
else:
end = middle - 1
else:
if start_val <= target < mid_val:
end = middle - 1
else:
start = middle +1
return -1
这是一道经典问题,借助了二分查找的思想,充分利用上下文的输入,复杂度是‘O(n longn)‘. 看似无序的搜索问题,其实在二分搜索的时候可以在搜索空间内进行剪纸,从而最大的减少复杂度。