图
本章节主要介绍图相关的算法,例如图的深度搜索和广度搜索,这个在我们的生活中是十分常见的一个场景,例如迷宫,如何找到走出迷宫的路径等等。
本文操作的基础图如下
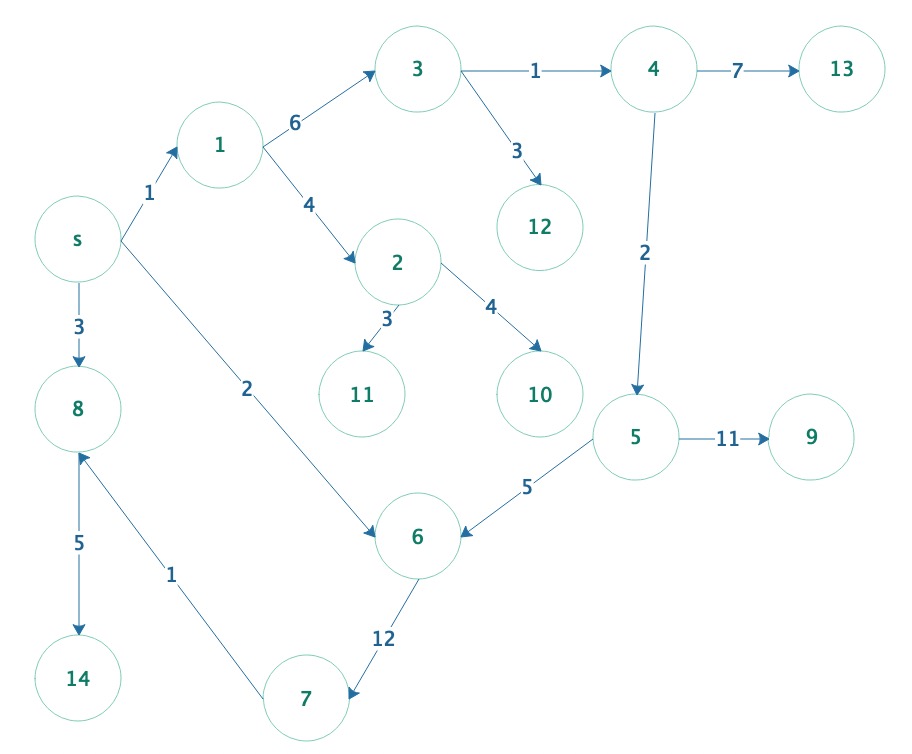
深度搜索
class Graph(object):
def __init__(self, graph={}, start="s"):
self.graph = graph
self.start = start
def deep_traverse(self):
stack = list()
deep_list = list()
stack.append(self.start)
while len(stack) > 0:
top = stack.pop()
if top in deep_list:
continue
else:
deep_list.append(top)
if self.graph.get(top) is not None:
stack.extend(self.graph.get(top))
return deep_list
提到深度优先搜索不管是图还是树如果不使用递归一般都是使用堆栈来模拟这个过程,这里说一下,如果能不使用递归尽量不要使用递归,代码执行逻辑比较难懂。
deep_list用来保存遍历后的序列,stack用来一层一层的存储遍历以后的结果,深度搜索都是优先访问当前节点的孩子节点,所以正好符合堆栈的性质,后进来的可以先出去将孩子节点放入stack中。
图的广度搜索
def breadth_traverse(self):
q = Queue()
breads_list = list()
q.put(self.start)
while not q.empty():
queue_head = q.get()
if queue_head in breads_list:
continue
else:
breads_list.append(queue_head)
if self.graph.get(queue_head) is not None:
for child in self.graph.get(queue_head):
q.put(child)
return breads_list
与深度优先相对应就是广度优先搜索,这里使用队列来模拟广度优先搜索,如果你对数据数据的样式有疑问可以看下面的代码地址。
这里是用一系列的映射关系来表示一个图的。
单源最短路径
def dijkstra(self):
q = PriorityQueue()
path_dict = {"s":0}
q.put((0, self.start))
while not q.empty():
head = q.get()[1]
children = self.graph.get(head)
if children is None:
continue
for idx, child in enumerate(children):
w = self.weight.get(head)[idx]
q.put((w, child))
if path_dict.get(child) is None:
path_dict[child] = w + path_dict[head]
else:
tmp = w + path_dict[head]
if tmp < path_dict[child]:
path_dict[child] = tmp
print path_dict
单源最短路径算法,这个算法有一个禁忌就是权重不能为负值,否则出现的结果可能会不准或是出现死循环。
这里借用一个优先队列的概念,我们q里的数据都会选择权重较小的值开始遍历,path_dict是存储最短路径的字典,C++中一般会使用数组来做,然后不断的遍历当前节点的孩子节点和权重,如果出现新的路径权重小于原有的权重就进行一次更新。
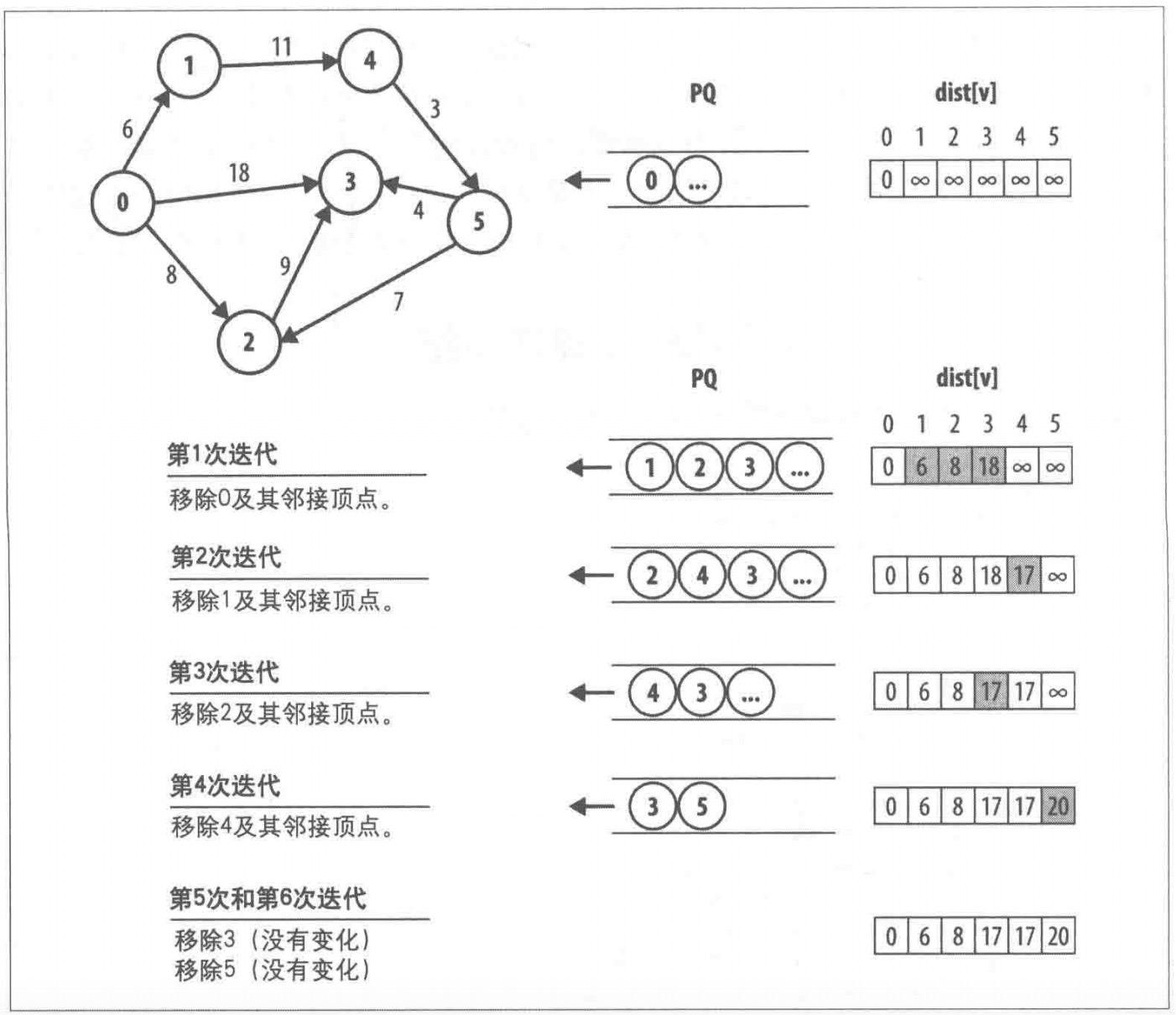
上面这个图片很清楚的讲述了遍历的序列,大家可以看看。
复杂度分析
算法复杂度是$O(V^2+E)$,其中V是点数,E是边的数量
##改进的单源最短路径
通过上面的描述我们知道,普通的单源最短路径算法是有一个弊端的,就是不能出现负的权重,这在我们的生活中是不现实的,例如我们选择一条路径对于到达目的地是负收益的。
算法复杂度
改进后的算法复杂度为$O(VE)$
代码地址