GRAPH ATTENTION NETWORKS
图注意力神经网络是既GCN神经网络后,有一个图结构深度学习的网络,本节我们来学习。原文地址可以点击GRAPH ATTENTION NETWORKS下载。
在原来的GCN神经网络中,我们能够理解到GCN是存在一定的局限性的,在如下的场景下。
- GCN无法完成处理动态图的任务,既训练和测试在不同的图网络中。
- 处理有向图是有瓶颈的,不容易实现分配不同的学习权重给不同的neighbor。
针对这样的问题,本文提出了一种新的网络机构就是基于注意力的图网络。
graph attentional layer
首先我们需要看一层graph attentional layer 是如何计算的。
对于单个的graph attentional layer的输入是一个节点特征向量集合。
h={h1,h2,h3,..,hn}(1.1)
其中hi∈RF,N表示节点邻居节点的个数,F表示相应的特征向量的维度,就是每个节点的特征。每一层的输出是一个新的节点特征向量集。
h′={h1′,h2′,h3′,..,hn′}(1.2)
其中,F′表示新的节点特征向量的维度。
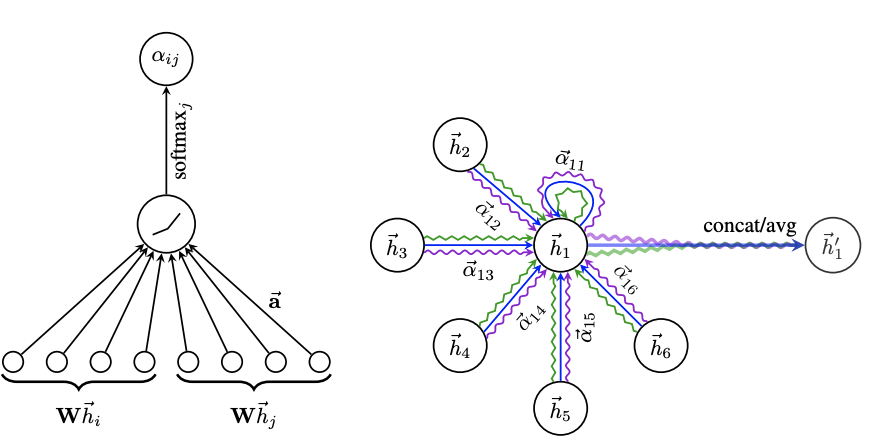
具体的graph attentional layer首先根据输入节点的特征,进行self-attention处理
eij=a(Whi,Whj)(1.3)
其中a表示一个RF′×RF′→R 的映射。W∈RF′×F是一个权值矩阵,一般来讲self-attention将注意力分配到图中所有节点,这种做法是会丢掉信息的。本身使用了masked attention的方式将注意力分配到邻居节点上。j∈Ni.
aij=softmax(eij)=∑k∈Niexp(eik)exp(eij)(1.4)
本文中,a是单层前馈神经网络,总共的计算过程是
aij=∑k inNiexp(LeakyRelu(aT[whi∣∣Whk]))exp(LeakyRelu(aT[Whi∣∣Whj]))(1.5)
其中aT∈R2F′为前馈神经网络的a的参数。
hi′=σ(j∈Ni∑aijkWkhj)(1.6)
为了提高模型的拟合能力,在本文中还引入了多抽头的self-attention。
hi′=∣∣σ(j∈Ni∑aijkWkhj)(1.7)
其中∣∣表示连接,aijk和WK表示k个抽头的计算结果。由于Wk∈RF′×F,因此这里的hi′∈RKF′。同样可以采取求和的方式得到hi′
hi′=σ(K1k=1∑Kj∈Ni∑aijkWkhj)(1.8)
总结
- 与GCN的联系与区别?
GCN与GAT都是将邻居顶点的特征聚合到中心顶点上(一种aggregate运算),利用graph上的local stationary学习新的顶点特征表达。不同的是GCN利用了拉普拉斯矩阵,GAT利用attention系数。一定程度上而言,GAT会更强,因为 顶点特征之间的相关性被更好地融入到模型中。
2.为什么GAT适用于有向图?
我认为最根本的原因是GAT的运算方式是逐顶点的运算(node-wise),这一点可从公式(1.3)—公式(1.6)中很明显地看出。每一次运算都需要循环遍历图上的所有顶点来完成。逐顶点运算意味着,摆脱了拉普利矩阵的束缚,使得有向图问题迎刃而解。
其核心问题就是,GCN使用拉普拉斯矩阵的缘故,将图的结构合并成一个度矩阵然后计算,所以对每个节点不会特殊学习。