基于值的深度强化算法
今天要介绍的Dueling DQN网络是对于网络架构而非算法的改进,之前的章节中提到过,通过优化动作-优势函数(A(s,a))利用状态值函数V(s)和动作值函数Q(s,a)之间的联系优化学习过程。
Dueling DQN
Dueling DQN(竞争强化网络)的思路是将原始的Q值,拆成两个部分,一部分是动作无关的值函数V(s),另一个是在这个状态下各个动作的优势函数A(s,a)。
Q(s,a)=V(s)+A(s,a)
其中V(s)可以理解为在该状态s下,所有可能得动作说对应的动作值函数乘以采取该动作的概率之和。通俗地说,值函数V(s)是该状态下所有动作值函数关于动作概率的期望。而动作值函数Q(s,a)是单个动作所对应的值函数,Q(s,a)-V(s)表示当前动作值函数相对于平均值的大小。所以,优势表示的是动作值函数相比于当前状态值函数的优势。如果优势函数大于0,则说明当前动作比平均动作好,如果优势函数小于0,则说明当前动作不如平均动作好。优势函数表明的是在这个状态下各个动作的相对好坏程度。如图1-1
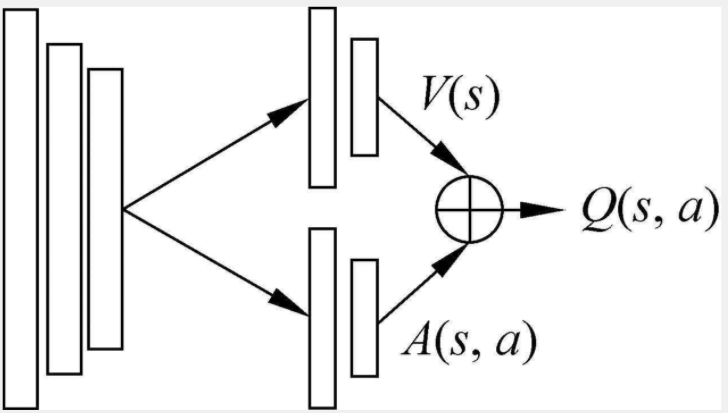
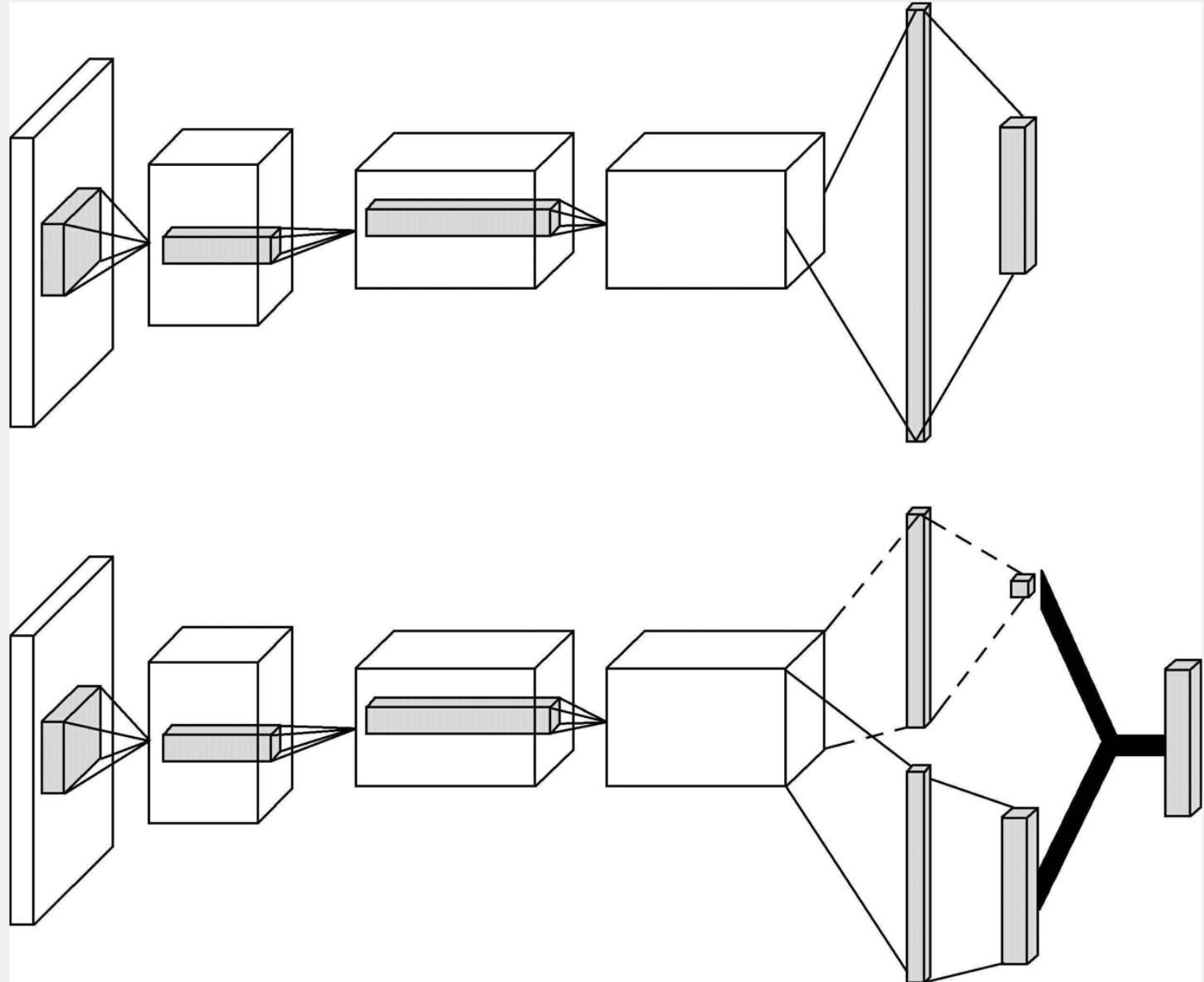
下图让我们看下一个Dueling DQN和传统DQN网络的区别,这个也是唯一的区别。主要的区别是在末尾出的特征拆解,上路用于预测值函数V,表示静态状态空间的本身具有的价值,一部分用于预测a,表示选择动作以后获得的额外价值。然后汇聚到一起预测A的分布。其实我们发现实际的值函数是两部分的组合,而这两部分都是未知数,又有无数种组合,如果你按照这样做会发现很少能够符合情理。所以在实际的工作中,所以要对A进行限定,强制令所有选择贪婪动作的优势函数为0.
Q(s,a,θ;α,β)=V(s;θ,β)+(A(s,a;θ,α)−maxAa′∈A(s,a′,θ,α))
这样我们就能固定值函数,
a∗=argmaxQ(s,a′,θ,α,β)=argmaxA(s,a′,θ,α)Q(s,a∗,θ,α,β)=V(s,θ,β)
因为同一个状态值函数是确定的,与行动无关,不会随着行为变化而变化,这样学出来的V和A更加具有实际的意义。
在实际中,一般使用优势函数的平均值代替上述的最优值。大量实验表明,两公式实验结果非常接近,但是很明显平均值公式比最大值公式更加简洁。
Q(s,a,θ;α,β)=V(s;θ,β)+(A(s,a;θ,α)−A1a∈actions∑A(s,a′;θ,a)
然平均值公式最终改变了优势函数的值,但是它可以保证该状态下在各优势函数相对排序不变的情况下,缩小Q值的范围,去除多余的自由度,提高算法的稳定性。
同时,需要注意的是平均值公式是网络的一部分,不是一个单独的算法步骤。与标准的DQN算法一样,Dueling DQN也是端对端的训练网络,不用单独训练值函数V和优势函数A。通过反向传播方法,V(s;θ,β)和A(s,a;θ,α)被自动计算出来,无须任何额外的算法修改。由于Dueling DQN与标准DQN具有相同的输入和输出,因此可以使用任何训练DQN的方法(如DDQN和Sarsa)来训练决Dueling DQN。
标签
状态值函数(V值)的标签:
V值表示在当前状态 s 下,采取任意动作的期望回报。在训练过程中,我们使用目标Q网络来估计V值,即使用目标Q网络的输出来表示状态值函数。
优势函数(Advantage值)的标签:
优势函数表示在当前状态 s 下,采取动作 a 相对于采取其他动作的优势。为了计算优势函数的标注,我们需要使用目标Q网络来估计目标Q值,并从中减去V值。
试用场景
在一般的游戏场景中,经常存在很多的状态,但是采用什么样的动作对下一步的状态转换没有什么影响,这些情况下计算动作的价值函数就没有计算状态价值函数的意义大,在频繁出现智能体采用不同的动作但是对应的值函数相等的情况下,Dueling DQN的优势会有表达的优势。
总而言之
综上所述,相对于传统的网络结构来说,Dueling DQN将Q值分解为值函数V和优势函数A这种形式,使得训练更容易,收敛速度更快。当动作的数量增加时,其优势就越明显。状态值函数V的部分只依赖于状态,和行为无关,训练起来更容易;且同一状态下,多个行为可共享一个值函数V。不同行为之间的差别只体现在优势函数A部分。这部分的收敛也可以与值函数V独立开来,使得行为之间的相对差别可以独立学习。并且优势函数的引进,避免了因为Q值的量级大,而Q值之间差异非常小,而引起的结果不稳定问题。