RankNet
RankNet是一种pairwise的排序方法,它将排序问题转换为比较<di,dj>对的排序概率问题,即比较di排在dj前面的概率。RankNet提出了一种概率损失函数来学习排序模型,并通过排序模型对文档进行排序。这里的排序模型可以是任意对参数可微的模型,如增强树、神经网络等。
模型训练完毕后模型对每个样本给出一个预测值p,然后通过计算损失函数来对模型进行调整。RankNet中定义了两个概率来分别表示预测值和标签值,分别是预测相关性概率和真实相关性概率.
一般训练数据是按查询划分的,对每个查询内部数据进行排序,RankNet通过评分函数f(x)对输入的特征向量进行评分。对于给定的查询,选择具有不同标签的文档Di和Dj,并将其特征向量xi和xj输入给模型,分别计算得分vi=f(xi)和vj=f(xj),通过sigmoid函数将两得分映射为一个学习概率,即Di比Dj更相关的预测概率为
pij=p(Di<Dj)=1+e−σ(vi−vj)1
其中Di<Dj表示Di排在Dj前面,参数σ确定sigmoid函数形状,由此便得到了预测相关性概率。
接下来看下真实相关性概率。
每个文档对中的文档Di和Dj均包含一个表征与该查询相关性的标签,如Di关于该查询的标签为非常相关,Dj为不相关,很明显Di比Dj更相关。因此,真实相关性概率定义为
pij=21(1+Vij)
如果Di比Dj更相关,则Vij=1;如果Dj比Di更相关,则Vij=−1;若其标签值相等,则Vij=0。
像其他pairwise方法一样,RankNet会评估所有文档对的相对关系,以错误的文档对最少作为优化目标。RankNet引入了概率的思想,优化目标转换为预测相关性概率与真实相关性概率的差距最小。RankNet采用交叉熵作为损失函数,公式如下:
loss=−pijlogpij−(1−pij)log(1−pij)
将预测相关性概率公式和真实相关性概率公式代入损失函数,则有
loss=21(1−Vij)σ(vi−vj)+log(1+e−σ(vi−vj))
当Vij=1的时候,
loss=log(1+e−σ(vi−vj))
当Vij=−1的时候,
loss=log(1+e−σ(vj−vi))
当Vij=0的时候,
loss=log2
由此可以看出,两个排序不同的文档即使评估分值相同,损失函数也会对其进行惩罚。并且如果分数与实际排名不符,则损失函数为类线性函数;如果相符,则损失函数为0。对vi和vj分别求导:
∂vi∂loss=−∂vj∂loss
以上梯度可以用于更新模型参数.
LambdaRank
RankNet主要针对文档对相对顺序关系的错误数量进行优化,而并不区分不同文档在优化时的权重。在重点关注头部排序的场景下,效果并不理想,如以NDCG作为评估指标,此时模型拟合应更关注于排序靠前的文档,但RankNet的优化目标与实际的优化目标是有偏差的,因此不能取得很好的效果,RankNet没办法以NDCG这些指标作为优化目标进行迭代。以图1为例,其表示一个给定查询的二分类有序文档集,圆形表示与查询相关的文档,正方形表示与查询不相关的文档。
对于RankNet而言,其损失函数cost通过文档对的错误数量来衡量。在图1-a中,cost为6(通过排序错误对数量计算得到);在图1-b(经过一轮优化后)中,将排序最靠前的相关文档下调2个位置,将底部的相关文档上调3个位置,此时cost为5。但是对于像NDCG等更注重头部排序的指标,这并不是其想要的结果。图1-b中的左边箭头代表RankNet的梯度方向和幅度,右边箭头代表真正需要的梯度方向和幅度,即更关注靠前位置的文档的提升。
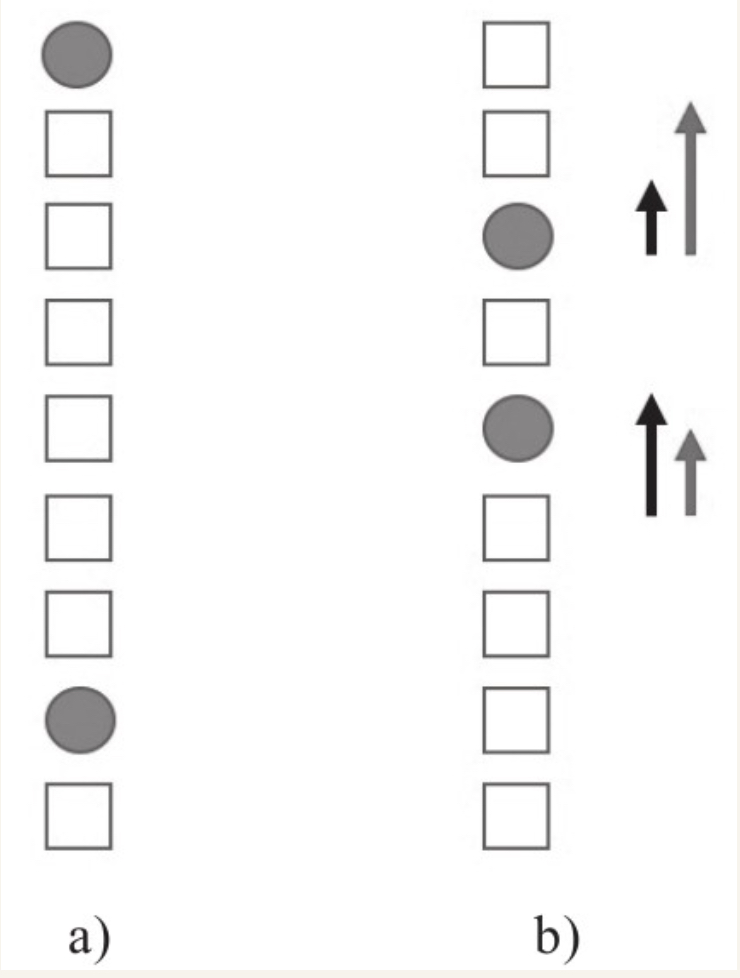
LambdaRank针对上述问题提出了一种经验算法,它不再像RankNet一样通过定义损失函数再求梯度的方式处理排序问题,而是直接定义梯度,即Lambda梯度,这样便可以解决大部分评估指标带来的问题。在训练模型时,我们不需要知道损失函数计算的代价本身,而只需要代价的梯度即可.