最近因为工作原因，需要重新回顾xgboost，原来我个人也仅仅限制于使用，没有过多总结，借着这次机会，正好回顾一下这款神器。提到xgboost就必须要提一下cart树，这个是xgboost的基本组成单元。
cart树
之前微博中提到决策树，可能包括ID3和cs4.5这些算法，其实cart树和这些算法没有什么本质的区别，都是找到一些分割点，然后构建决策树，这里我们主要介绍一下cart的细节，其实这个也是一些资料比较难以查到的。
咱们就话不多说，直接进入正题吧。
分类树生成
cart树的生成是自上而下的，从根节点开始，通过特征进行分裂。cart采用基尼指数进行特征选择的度量方式。
基尼指数的形式化表达如下
$$
Gini(D)=1-\sum_{k=1}^{k} p_{k}^{2} \tag{1.1}
$$
$D$表示样本集合，K表示类别个数，$p_{k}$表示类别k的样本占有所有样本的比值。基尼指数越小，样本分布越集中，当纯净到只有一类样本的时候，基尼指数为0，反之，样本分布越均匀，基尼指数就越大。对于二分类来讲
$$\begin{gathered}Gini(D)=1-\sum_{k=1}^{k} p_{k}^{2} \\
= 1-p_{1}^2-p_{2}^2 \\
=1-p_{1}^2-(1-p_{1})^2 \\
=2p_{1}(1-p_{1})\end{gathered}$$
基尼指数越大，标明经过A特征样本的不确定性越大。
通过最优特征和最优切分点对节点进行分裂，生成子节点，即将原样本集划分成了两个子样本集，然后对子节点递归调用上述步骤，直到满足停止条件。一般来说，停止条件是基尼指数小于阈值或者样本数小于一定阈值。
分类树的生成
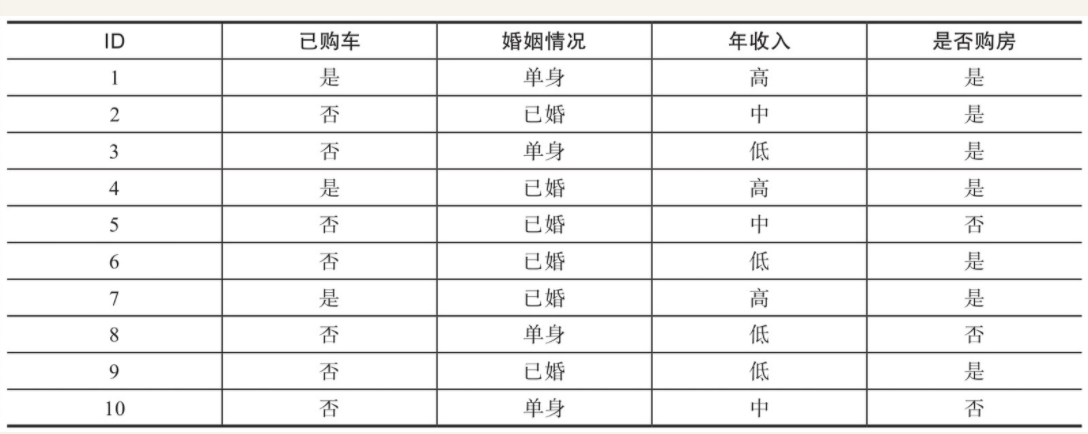
接下来我们来根据数据来看看cart树的分类过程。这是一个用户是否有意愿购房的数据。
可以看到，已购车的3个样本最终均购买了房产，而未购车的7个样本中，4个购买了房产，3个未购买房产。因此，已购车样本购买房产的概率$p_{1}=1$，
$$
Gini(1)=3 \times 1 \times(1-1)=0
$$
$$
Gini(2)=1 \times \frac{4}{7} \times (1-\frac{4}{7})=0.49
$$
以已购车特征为例，用$F_{1}$表示。1和0分别表示已购车和未购车。
$$
Gini(F_1=1)=\frac{3}{10} \times Gini(1) + \frac{7}{10} \times Gini(2)=0.343
$$
同理， 咱们求出类似的
$$
Gini(F_2=1)==0.367
$$
特征$F_{3}$有3个可能的取值，此处以1、2、3表示年收入的低、中、高，分
$$\begin{gathered}Gini(F_3=1)==0.417 \\
Gini(F_3=2)==0.305 \\
Gini(F_3=3)==0.343 \\ \end{gathered}$$
$Gini（F_{3}=2）$是特征$F_{3}$中基尼指数最小的，因此特征$F_{3}$的最优切分点为$F_{3}=2$.
综上所述，$F_{3}$是三个特征基尼指数最小的，就是最优特征。最终求得最优特征$F_{3}$以及最优切分点为2.
回归树的生成
回归树在预测值为连续值的时候又是怎样的呢？一般叶子节点所有样本的平均值作为该节点的预测值。cart树算法生成回归树的方法和生成分类树的方式不同，不再通过基尼指数进行特征选择。而是采用平方误差最小化。
回归树在进行。
- 从根节点开始分裂
- 节点分裂之前，计算所有可能的特征以及所有坑你的切分分裂后的平方误差
- 如果所有平方误差均相同或者减小到某一阈值，就停止分裂。否则选择平方误差最小的特征切分
- 对弈每个生成的新节点，递归2，3
小结
本章简单介绍了cart树的原理，接下来的章节就是我们要看看cart树在xgboost中是如何使用的。