今天我们来介绍经典的元学习方法MAML算法,首先我们需要明确MAML算法是用来做什么的呢?其实它主要是解决我们模型参数初始化的问题的,一个好的初始化是可以让我们快速达到全局最优并且训练成本也会骤降的,那么我们来看看MAML算法是怎么做的把?
算法讲解
这个算法的伪代码十分简单,咱们就对着源代码看看它的训练过程和使用方法。下面就是这个算法的伪代码啦。

这里重要的部分分别是4到7行和第8行,双重梯度的思路。
训练方法
首先我们从所有的数据集合中抽取出来N个任务,每个任务都包含训练集合(training set)和支撑集(support set)以及查询集合(query set)。这里需要说明的是,有些集合是会有重复出现,例如某些task的query set会成为某些task的support task。这个的数据集合才能让我们的元学习器有足够的能力应对更加陌生的任务。
那么,我们就要在上面这些数据上进行一次梯度训练啦,从众多task中抽取一部分(3行),进行一次梯度训练,对于每个任务都去更新我们的实际参数θ。这里需要注意的是我们仅仅进行一次梯度迭代。但是不进行参数的更新,只是记住累计误差θ′,经过这一波训练以后。就如下图一样,我们知道怎么去更新θ。
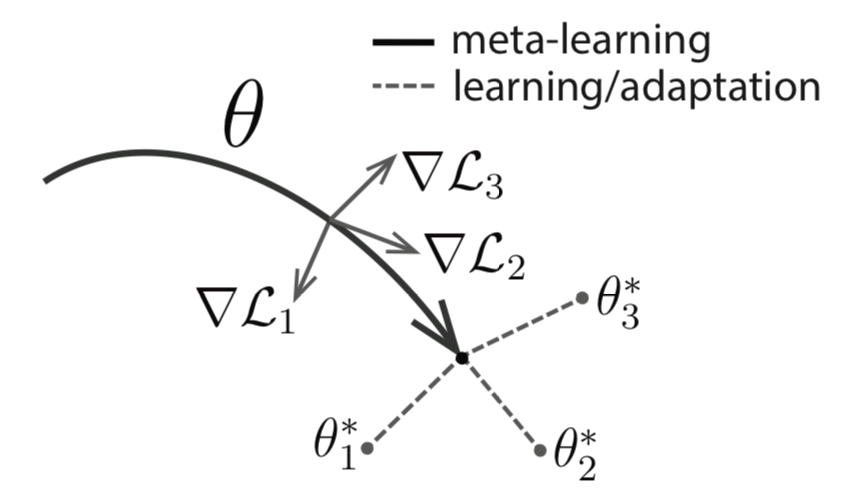
通过第8行的梯度迭代才真正的更新θ, 这个时候我们的模型实际上是结合了很多个任务以后决定梯度迭代的方向。说道这里似乎算法都都结束啦。
这里能够被大规模的推广也是因为算法足够简单且容易理解。所以MAML算法经常与其他学习方式结合变成一个新的领域方法。例如元强化学习,元模拟学习等,就是为了解决在强化学习中环境随着动作的执行,环境也在改变的情况。
模型使用
这里一肯定会问,这玩意一堆操作看着挺悬的,我咋样呀?其实使用的时候和预训练的时候十分相同,我们仍然对着上面的算法说。
步骤1中的参数θ不用随机初始化啦,使用我们的大众参数进行初始化即可。
步骤3中我们可以直接使用这样的参数使用支撑集进行训练,使用查询集合进行验证就可以啦。因为我们的初始化参数足够好,所以不用担心支撑集小的问题,能够快速模型收敛。
步骤8就没有啦,因为我们已经成为一个武林高手啦,忘记师傅是谁啦。(😄😄)
总而言之
其实MAML算法的核心是想让我通过大量的学习任务学习到一个公共的先验信息,在新的任务上我们直接做小样本的学习就能够解决我们的问题,省了很多的麻烦。