本章节中我们来介绍一个具有适应能力的神经网络学习框架CSN，接下来咱们就来看看这个网络是如何学习的。

网络整体架构

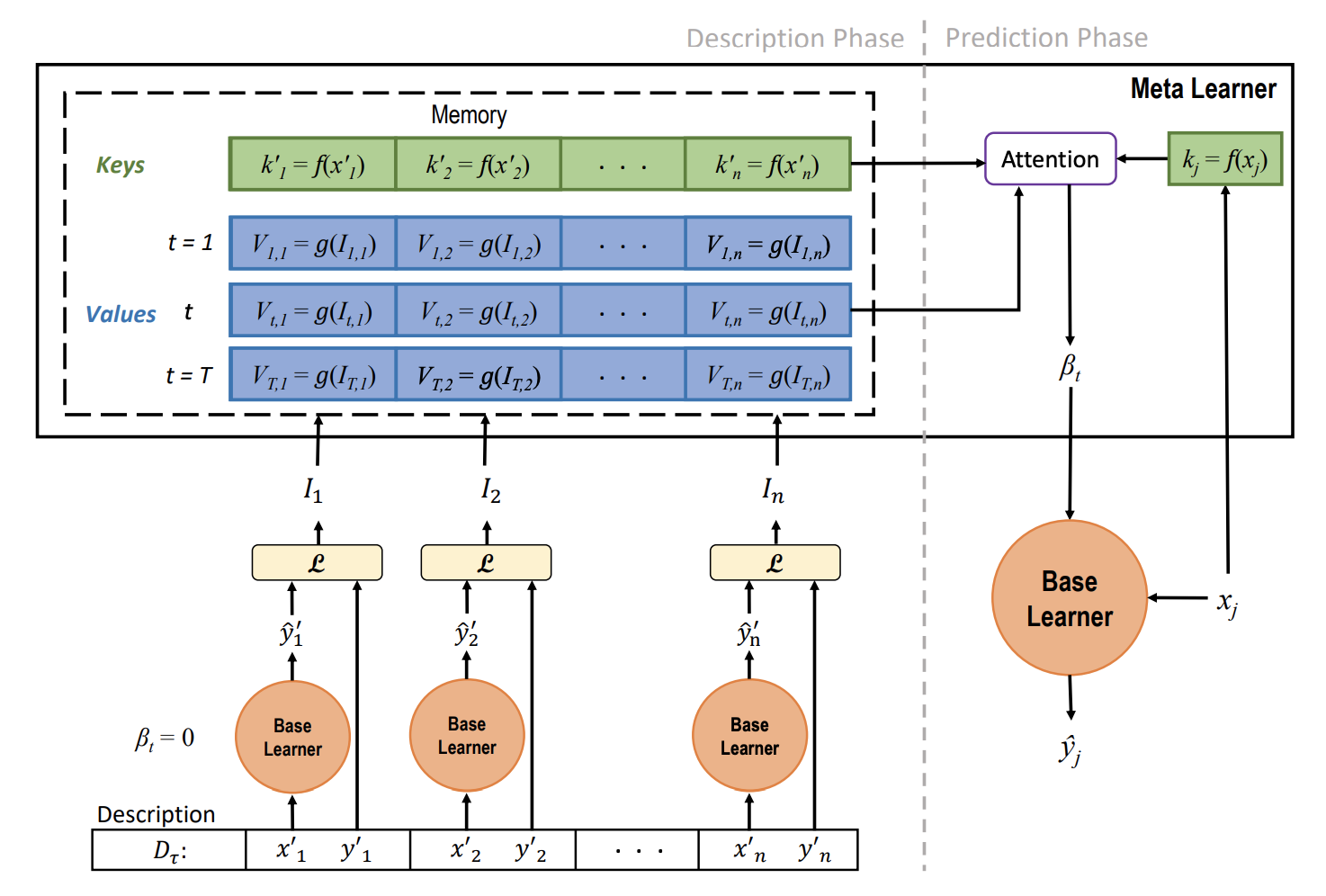
上面这个图是整个学习框架的整体架构，接下来我们来一点一点的讲解其中的细节。
假设我们一大批数据的训练任务已经训练好，突然来了一个新的任务，怎么把我们已经训练好的网络进行一定的复用快速的应用到新任务呢？这就是本文一个要解决的问题。

h_{t}= \begin{cases} \begin{align} \sigma(a_{t})+\sigma(\beta_{t})\ t≠T\\ softmax(a_{t}+\beta_{t})\ t=T\\ \end{align} \end{cases} \tag{1.0}

这里的T表示网络的最后一层，$\sigma$表示非线性转换，$a_{t}$表示的是激活层的前一程输入，$\beta_{t}$就是本章要讲解的重点，网络专属参数。也就是训练网络的时候，为每个专属的任务构建一个专属的参数，那么在应对新的任务的时候，我们只需要构建这个专属的参数就能快速的适应新的任务。从上面的概图上能够看出一个学习里包含两个阶段，一个是描述阶段，一个是预测阶段。

描述阶段

在描述阶段，我们来构建基础学习器（base learner），这个阶段就是针对每个分类任务进行常规的学习，$D_{t}$表示的是一个任务，举例就是分类一个仙人掌和一个菊花就可以称为一个任务。这个训练过程中需要产生一个信息，称为条件转换（conditional shifts），也就是上文提到的$\beta_{t}$,上图中的t表示每个任务的网络层数，对于每个网络层数提取$V_{t,i}$,表示第i个学习任务的第t层网络参数。需要说明一下的是，这里使用的是基础学习器，激活已经包含上文的示例函数的表示形式啦，只不过$\beta_{t}=0$。

$$V_{t,i}=g(I_{t,i}) \tag{1.1}$$

公式1.1中的$I_{t,i}$表示条件信息，一般计算条件信息的方式有两种形式，

损失条件信息

$$▽_{t,i}=\frac{\partial L(y_{i},y_{i}')}{\partial a_{t}}$$

t表示网络的第几层，$a_{t}$表示第t层激活层之前的输入，整个公式想要表达的是基础训练器上使用损失函数和前层输出的一阶导数作为损失条件信息。更加合适的以下的表达。

I_{t,i,l}= \begin{cases} \begin{align} (\frac{log(v_{t,i,l})}{p},sgn(▽_{t,i,l}))\ v_{t,i,l}>e^{-p} \\ (-1, e^{p}v_{t,i,l})\ otherwise \end{align} \end{cases}

这里p是超参数，一般是7，这样就起到一个平滑的作用，条件信息中只包含条件信息，如果这个值太小就放大，如果太大就取log计算，起到一个平滑的作用。

直接反馈信息

接下来我们来介绍另一种计算条件信息的方式，直接反馈信息。

$$I_{t,i,l}=\sigma'(a_{t,l})(\vec{y}'_{i}-y'_{i})$$

$\sigma'(a_{t,l})$表示非线性激活层的一阶导数，$\vec{y}'_{i}-y'_{i}$表示基础学习器的损失函数对softmax输出层的一阶导数

通过上面任何一种方式我们都获取的$I_{t,i,l}$的计算值,接下来我们来来说说这个函数g应该怎么计算。其实这里的g函数并没有参与训练，使用一个MLP进行一个记忆映射，原文也提到想让全文都使用一个g函数就可以啦。所以这个计算的关键就是直接反馈信息。

python
csn_gradients = {
“conv_1”: tf.reshape(self.cnn_train.gradients[“conv_1”][0], [-1, 27 * 27 * 32, 1]) * tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=1),
“conv_2”: tf.reshape(self.cnn_train.gradients[“conv_2”][0], [-1, 26 * 26 * 32, 1]) * tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=1),
“conv_3”: tf.reshape(self.cnn_train.gradients[“conv_3”][0], [-1, 25 * 25 * 32, 1]) * tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=1),
# “conv_4”: tf.reshape(self.cnn_train.gradients[“conv_4”][0], [-1, 24 * 24 * 32, 1]) * tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=1),
“logits”: tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=2) * tf.expand_dims(tf.gradients(self.train_loss, self.cnn_train.logits)[0], axis=1),
}

上面的代码就是计算直接反馈条件信息的流程。
那么我们在描述成以下的任务。

1. 每层的记忆构建
2. 元学习器在元训练集合的特征提取
   这里还没有说道的就是元训练集合的特征提取，也就是最上层的k的计算，这里原文使用的是一个MLP的提取器，将原始的图片进行embedded。

预测节点

我们拿到了描述节点的输入，接下来就是如何预测小数据集上的图片呢？还是看上图，我们通过元学习器将新的图片进行特征提取。

$$k_{j}=f(x_{j})$$

f就是上文提到的MLP提取器， 然后使用一个attention的方法从以往学习的任务中抽取经验$\beta_{t}$.

$$\alpha=softmax(cos(k_{j}, k_{i}))$$

这个参数$\alpha$表示从每层抽取的权重分布。

$$\beta_{t}=\alpha * V_{t}$$

这样我们通过基础学习器调整每一层的参数$\beta_{t}$就能够学习新的知识，这样我们在进行新的任务学习的时候,就使用公式1.0的形式进行快速推理，从而完成新的任务，这里新的任务就是又完成一个新的分类任务。

总而言之

我们发现这个方法实际上巧妙的获取了以往学习的经验并应用到新的学习任务上，那么也带来了一部分问题，问题1就是还是需要使用大量的学习数据且十分依赖标注。问题2就是随着记忆模块信息的膨胀，信息会极度冗余。

Rapid Adaptation with Conditionally Shifted Neurons