元学习(零)--预训练神经网络

从本章节开始我们准备进入一个新的领域进行学习，元学习（meta learning），听起来是不是屌屌的，确实是这样，这里我们不得不总结一下之前咱们介绍各种的学习方法，包括经典的学习方法和神经网络的学习方法，毫不意外的它们有一个共同且残酷的名字(Weak AI)，是的凡是针对一个特定的一个领域进行学习的，都可以称之为弱学习器。而本章节的介绍的一系列建模方法它们学习的方式和角度与之前的学习方法会有很大不同，元学习更多切入点是让模型学会学习，同时这类方法也被统一称为general AI，普世人工智能，与元学习并列的有持续学习和终身学习，也是general AI的领域。目前来讲这类人工智能因为落地较少，可能很多算法工程师都没有听说过，但是确实人工领域下一个进化的方向。我们习惯于使用大量的数据和复杂的模型堆砌一个好的模型，但是模型真的像人一样，能够通过观察总结规律然后做出决策这可能才能称为人工智能。好了，闲话不多说啦，咱们开始今天的算法吧。

数据集合

元学习一般将数据集分成两类，大型数据集的样本称为 support sets，少样本称为 query sets；将训练分成两个阶段，一次学习称为一个 epoch（整个数据集），首先在 support sets 上训练并更新一次梯度，接着用 query sets 基于 support sets 更新的模型再求一次梯度，本轮 epoch 的梯度更新与 query sets 上梯度更新方向一致。可以这么理解，support sets 的作用就是让模型有一个好的初始化，接着再用 query sets 对模型进行 fine-tune，使模型真正适用于任务场景。显然，大型数据集和拥有的少样本数据来自不同 domain，存在 distribution shift，大型数据集训练的模型在任务上只能得到次优的效果。而通过一次次 query sets 的"fine-tune"，模型就能很好地适应任务场景。

预训练神经网络

预训练神经网络主要的场景是解决分类过程中有一些样本比较少，很难通过直接学习的方式获得比较好的效果，这类问题怎么来解决呢？如果我们使用神经网络做分类器，无非就是将特征提取网络输出的特征向量a(x),将a(x)输入到分类器（全连接层+softmax）中，与全连接层中的权重参数W相乘，计算内积，再用softmax函数转化为概率值就完成了一个分类，训练的目标就是最大化 $a(x)*w_{y}$ 的值尽量大，表示x属于y的概率大。这里我们可以思考一下，对于一份数据集合例如图片分类的任务，前面各种卷积操作都是为了特征提取，这一部分一定是可以复用，如果我们想在一个模型中加入几种小样本的分类，前面特征提取的过程需要重新训练吗？这里我们可以给出一个结论，当然是不用的，也就是说添加一个新的分类的情况下，我们只要找到一个 $w_{y}$ 能够适配我们的新的类别是不是就可以使用呢？以上就是作者的一个大概的思路。通过上面的讲解也就是说需要训练出来的函数ϕ都能够稳定的表达 $s_{y}$ 和 $w_{y}$ 的映射，是不是说我们在新的类别上也能够使用这个映射函数快速的将新的类别预测好呢？其中 $s_{y}$ 表示输出层之前的一层激活后的参数， $w_{y}$ 表示输出层对于这个类别y的神经元参数。

算法整体流程

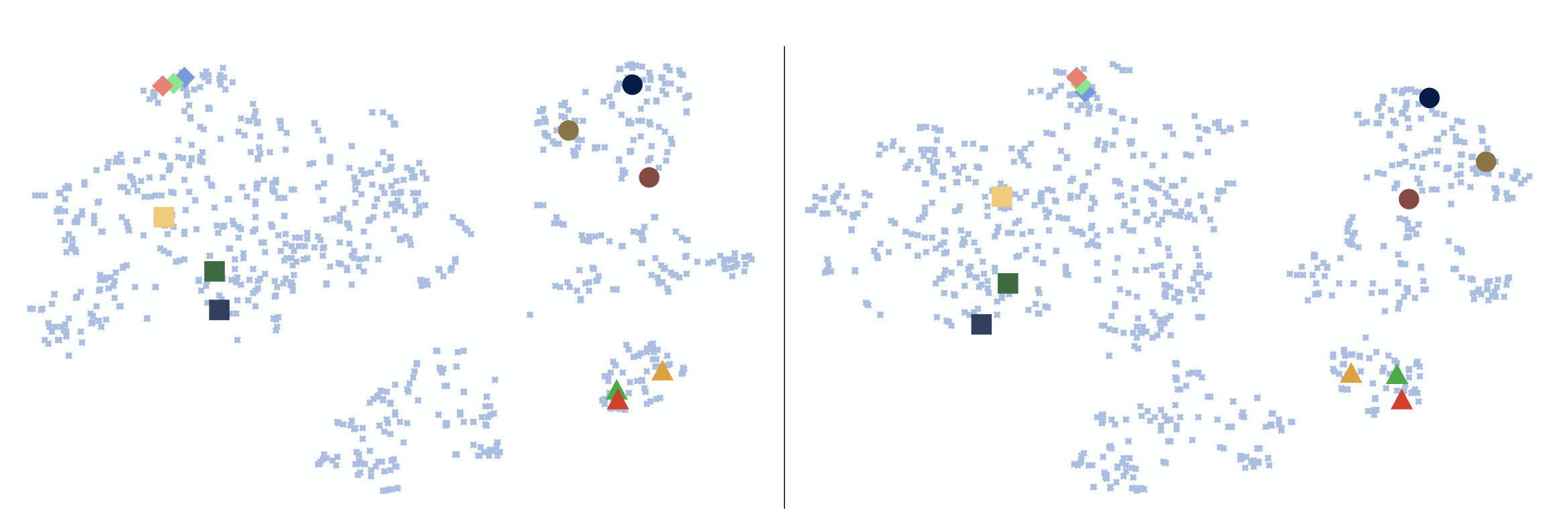
算法的整体流程比较复杂，下面我们来拆分一下训练和推理过程。首先我们训练的目标是想训练处一个映射关系ϕ，能够稳定的表达 $\bar{a_{y}} -> w_{y}$ ,这里的 $\bar{a_{y}}$ 表示属于y类别的图片embedding以后的均值向量，这里要说明一下，所里所谓的均值是将属于y类别的向量每一位去求和取均值，所以 $\bar{a_{y}}$ 是一个多维度的向量。之所以要做这样一个事情是因为想使用 $\bar{a_{y}}$ 作为分类的基准，因为同一类别的降维向量相似度也比较高，如下图所示。

训练

这个训练方法需要准备两个集合 $D_{large}$ 和 $D_{few}$ ，分别表示一个带有标注的大图片集合和一个小样本的小标注集合，这里的 $D_{few}$ 的数量可能每个类别下只有10张以内的样本。然后我们需要解决是 $D_{large}$ 下训练的模型怎么通用到 $D_{few}$ 的数集合上。

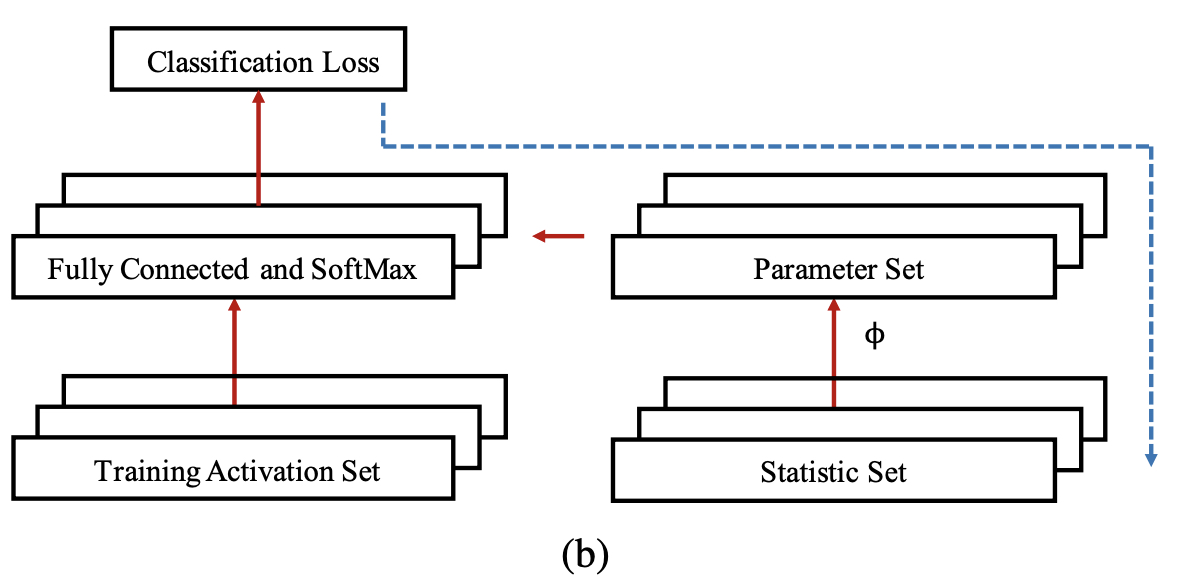
训练的第一步是在 $D_{large}$ 训练一个分类网络，原文使用的残差网络，实际应用中什么都可以的。这个网络可以把每个样本进行embedding降维。Training Activation Set通过 $D_{large}$ 数据集合进行采样，且每个类别采样1个样本，从 $A_{y} \cup \bar{a_{y}}$ 从抽取，也就是说每个类别可以抽取原始样本，也可以抽取这个分类样本的均值向量，同理Statistic Set也需要按照这样的抽样方式抽取。这样我们就有了两个集合。
Training Activation Set通过正常的训练过程，Statistic Set通过ϕ转化预测参数，然后预测好参数拷贝到左侧的全连接层然后计算分类损失，反向传播的时候更新的是ϕ预测器中的参数，是分类损失最小。所以这里的损失函数如下

L(ϕ)=\sum_{y,x \in D_{large}}=E[-ϕ(s_{y})a(x)+log \sum_{y' \in C_{large}} e^{ϕ(s_{y'}) a(x)}]+\lambda |ϕ|

其中 $s_{y}$ 表示Statistic Set的降维表示， $s_{y‘}$ 表示的是Training Activation Set的降维表示，可以发现这个损失函数是把每个分类都与其他的所有分类的和做了一次损失，也就是我们要找到一个函数ϕ使得当前的x属于y的分类概率最大，属于其他的分类的概率最小。这里对于分类y的采样可以以p的概率采样 $\bar{a_{y}}$ ，以1-p的概率采样 $A_{y}$ 中的任何一个。通过这样的操作，我们就能训练一个函数映射ϕ对于Training Activation Set的不同数据经过统一的参数预测后进行一个正确的分类。

推理

上面我们主要介绍了模型训练的过程，训练的过程中就是要训练一个函数ϕ使得预测的时候各个类别的差距最大，且具有较好的通用性。那么接下来一个问题就是我们训练一个这样函数ϕ怎么用到小的样本中呢？

我们使用如下的公式进行分类

p(y|x)=\frac{e^{E[ϕ(s_{y})a(x)]}}{\sum_{y' \in C} e^{E[ϕ(s_{y'})a(x)]}} \tag{1.1}

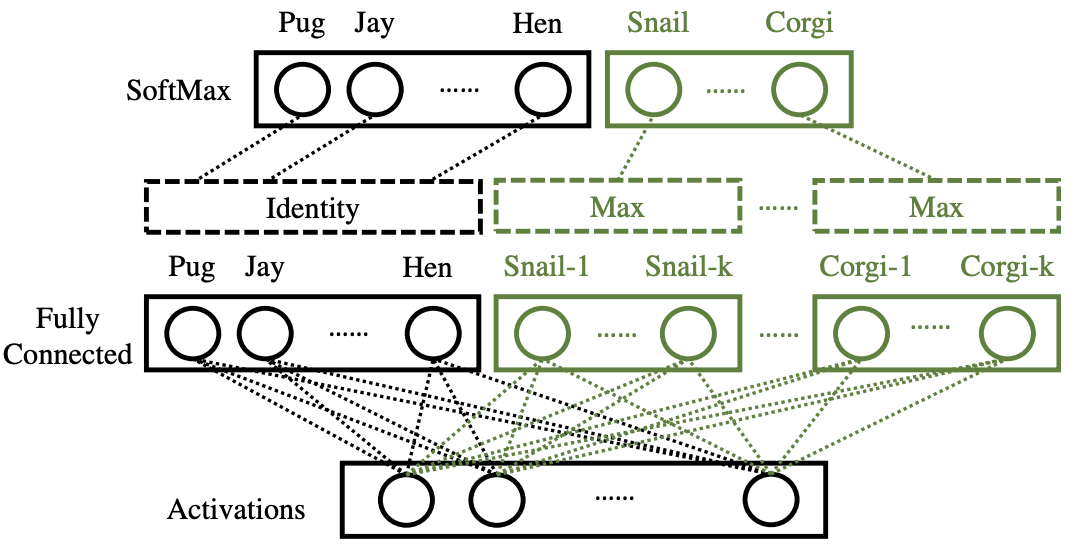
和我们训练时候的方式差不多，只不过这里因为添加了新的类别所以我们要使用当前的输入x与每个统计集合中每个类别的相似度作为一个概率输出。这里需要补充一下，统计集合中存放的是 $D_{large}$ 中的均值向量，以及 $D_{few}$ 中的均值向量，当然这里有个问题就是， $D_{large}$ 中的均值向量因为数据量巨大，所以置信度较高，但是对于few数据集来说，使用均值向量的时候 $\bar{a_{y}}$ 置信度并不高，所以当监测样本x的时候，会去比较“统计数据集合”中所有小样本集，一一对照，把相似度最大的作为最终的分类结果，如下图表示。