Fri Mar 1

人工智能因果推断定价策略

因果推断--uplift模型(二)

接下来这一章，咱们就来介绍一些基于深度学习的方法，当然这类方法理想情况下还是基于实验数据（RCT）进行训练。

反事实回归网络（CFR）

CFR其实是开启了使用深度学习的方式进行因果推断类任务的一个先河，我们知道，不同于观察模型，因果类的模型更关注与干预的影响，而非预测值的准确性，想要从理论上得到这个干预的效果，就一定要拉齐环境，或者随机数据进行对比，所以这个网络的设计上就需要满足两方面的要求。

具有拉齐函数的模块设计
还需要对目标值具有一定的拟合能力。
那么根据这两块的需求，就可以看看反事实回归网络的框架设计啦。

CFR结构解读

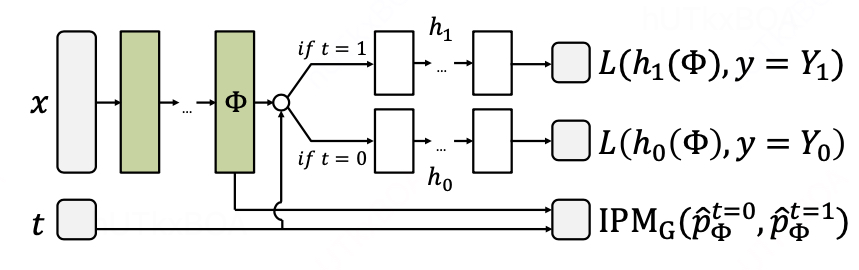
x是对于个体ITE的描述，经过一个Embedding的处理以后，就形成了共有的表示层 $\phi$ . 这个 $\phi$ 的物理意义更多是拉齐各种x的输入下的一个表示，用于拉齐环境。这个时候连接上t，也就是干预的动作，重新拟合Y的真值，当然这个过程引入了IPM进行分布的评估，需要确定在拉齐环境的基础上，进一步预测Y的真值。这样就有两个头预测不同场景下的真值，并且拉齐了环境。为了进一步学习干预t的影响，会拆分成两个隐层进行学习 $h_{1},h_{0}$ .
这里的IPM其实并不是唯一的使用刻画分布一致性的方式，只要能产生梯度都是可以的。

试用类型

在单treatment的情况下，CFR能够比较好的解决相关的问题。但是多treatment的情况下，需要一些修改。

伪代码解读

算法中第三行是先计算宏观数据的分布情况。6行计算IPM的梯度， 7行计算拟合梯度， 9行进行融合后进行反向传播。这里最后进行反向传播的时候会考虑权重的比例。
Estimating individual treatment effect: generalization bounds and algorithms

深度全空间交叉网络(DESCN)

DESCN是阿里同学的一个杰作，咱们就来分开看看这个DESCN的结构设计。首先给出来因果类的任务中经常面对的问题如下，这个DESCN模型能够某种意义上解决这类的问题，提升ATE的预估精度。
干预偏差：即存在倾向性分数，实验组和对照组的分布存在差异
数据不平衡：即实验组和对照组的样本量存在显著差异.

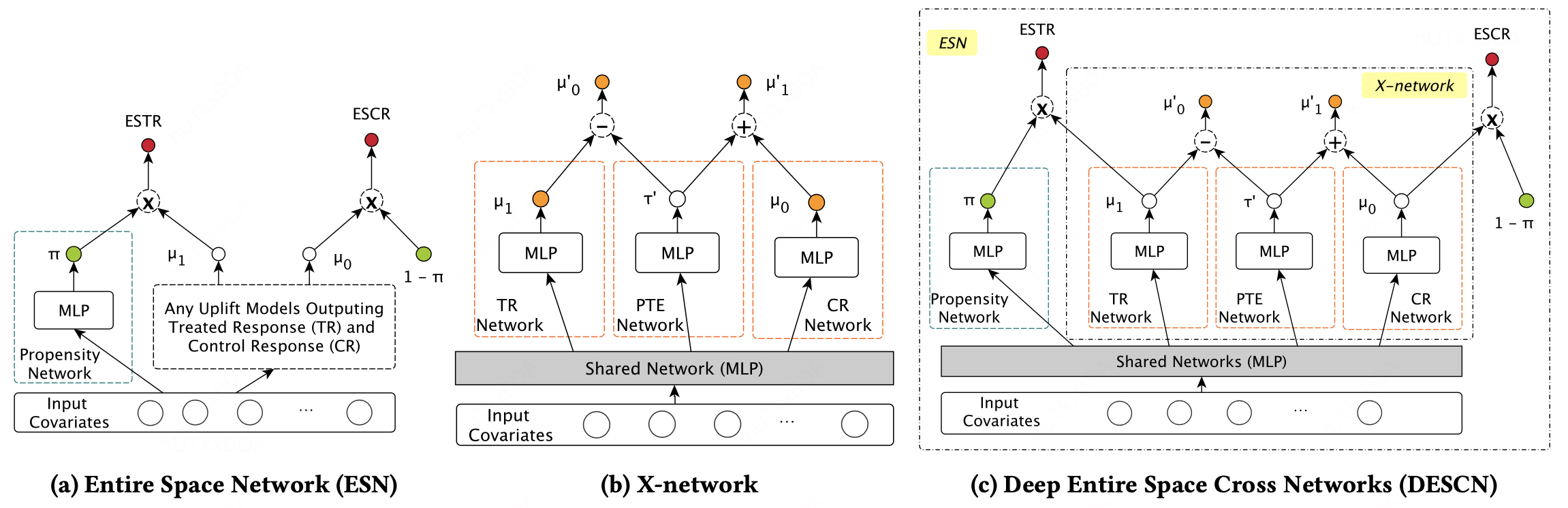
DESCN
上图是DESCN的整体的模型结构的。

ESN

ESN是将倾向性分数，实验组，对照组的建模放在一个模型中，通过共享层对不同的数据提取embedding。然后，对于每个数据计算倾向性得分π，对实验组数据进入干预分支得到ESTR(EntireSpace Treated Response)，对于对照组数据进入对照分支得到ESCR(Entire Space ControlResponse)。
然后我们来看看在因果的体系下， ESTR和ESCR分别表示什么。

\underbrace{P(Y|W=1,X)}_{ESTR}=\underbrace{P(Y|W=1,X)}_{TR} \underbrace{P(W=1,X)}_{π} =\mu_{1} π \\ \underbrace{P(Y|W=0,X)}_{ESCR}=\underbrace{P(Y|W=0,X)}_{CR} \underbrace{P(W=0,X)}_{1-π}=\mu_{0} (1-π) \tag{1.1}

损失函数也是分为如下的几部分。

L_{π}=\frac{1}{n} \sum_{i} l(w_{i},\hat{π}(x_{i})) \\ L_{ESTR}= \frac{1}{n} \sum_{i} l(y_{i} \& w_{i}, \hat{\mu_{1}}(x_{i}) \cdot \hat{π}(x_{i})) \\ L_{ESCR}= \frac{1}{n} \sum_{i} l(y_{i} \& (1-w_{i}), \hat{\mu_{0}}(x_{i}) \cdot (1-\hat{π}(x_{i}))) \tag{1.2}

l表示损失函数，一般是交叉熵损失函数， $\mu_{1}，\mu_{0}$ 表示模型输出。1或者是0表示实验组还是对照组。
最终的损失函数是公式1.2的三项的加权和。

X-network

现在我们来看X-network的具体动作，这里需要介绍的是图中PTE网络的作用，这里 $\tau$ ‘指的X-Learner中的填充疗效的作用。这里可以看X-learner相关的内容。这样我们通过 $\tau$ ‘就把TR和TC建立了联系和一个表达的形式。从而也解决实验组和对照组隔离的问题
这个 $\tau$ ‘会以加减的方式合并到 $\mu'$ 中。最终整个损失函数如下

L_{TR}=\frac{1}{|T|} \sum_{i \in T} l(y_{i},\hat{\mu_{1}}(x_{i})) \\ L_{CR}=\frac{1}{|C|} \sum_{i \in C} l(y_{i},\hat{\mu_{0}}(x_{i})) \\ L_{CrossTR}=\frac{1}{|T|} \sum_{i \in T} l(y_{i},\hat{\mu_{1}'}(x_{i})) \\ =\frac{1}{|T|} \sum_{i \in T} l(y_{i}, \sigma(\sigma^{-1}(\hat{\mu}_{0}(x_{i}))+\sigma^{-1}(\hat{\tau'}(x_{i})))) \\ L_{CrossCR}=\frac{1}{|C|} \sum_{i \in C} l(y_{i},\hat{\mu_{0}'}(x_{i})) \\ =\frac{1}{|C|} \sum_{i \in C}l(y_{i}, \sigma(\sigma^{-1}(\hat{\mu}_{1}(x_{i}))-\sigma^{-1}(\hat{\tau'}(x_{i})))) \tag{1.3}

结合上面所有的损失损失，给出 $L_{DESCN}$

L_{DESCN}=L_{ESN}+\gamma_{1} \cdot L_{CrossTR}+\gamma_{0} \cdot L_{CrossCR} \\ =\alpha \cdot L_{π}+\beta_{1} \cdot L_{ESTR} + \beta_{0} \cdot L_{ESCR} + \gamma_{1} \cdot L_{CrossTR}+\gamma_{0} \cdot L_{CrossCR}

到现在，整个网络都已经介绍完了，还是一个很巧妙的设计。

DragonNet

DragonNet也同样增加了了一个对干预变量T的预测头，这样做能够去除掉X中与T无关的一些变量，进而起到信息过滤的作用。

网络结构

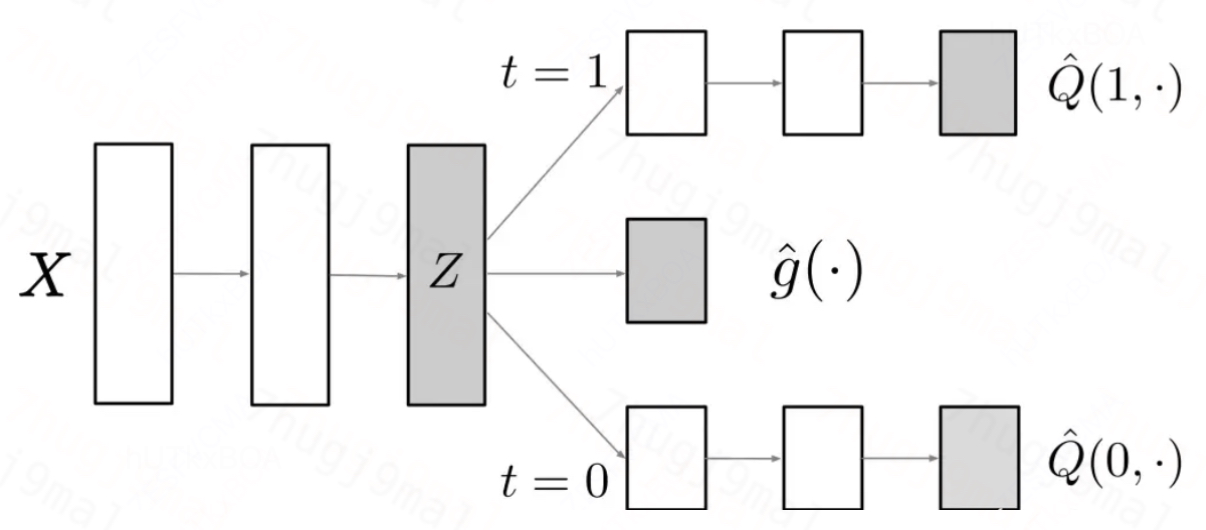
损失函数

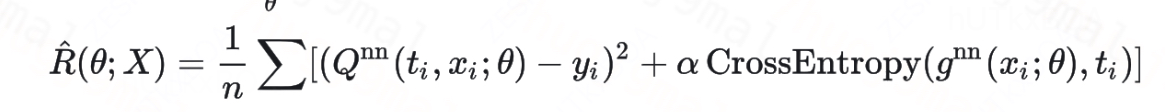
可以看到对于T的预估也通过交叉熵的方式进入了最终的损失函数，这个项能够对公用变量X起到矫正的作用。其实通过模型结构也能够看出来，相比与TarNet增加了一个对干预动作T的预估，因为引进了一个拟合头，所以相比与TarNet的仅仅拟合 $Y(0),Y(1)$ 的拟合成本是更大，所以预测精度会变差，另一方面相比于TarNet的设计，DragonNet明确了T的预测，并通过T的预测头矫正Z的表达，能够增强干预效果的学习，此外DragonNet 能够通过对干预状态的预测更好地捕捉不同特征下的异质性效应，提供更精确的 treatment effect 估计。

代码实现

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
from torch.utils.data import DataLoader, TensorDataset
import pandas as pd
import numpy as np

# 加载数据
df = pd.read_csv('./raw_avg_3day_reward_10day_data_20230630_20240301_label.txt', sep='\t', header=None, encoding='utf8',
                 converters={'0': str})
df = df[df[1].astype(str).str.contains('^(?!300).*$')]
idx = -1
X = df.iloc[:idx, 2:-1].values
Y = df.iloc[:idx, -1].values
T = np.random.binomial(1, 0.5, size=(len(Y),))  # 模拟干预变量，随机0或1

# 数据拆分
X_train, X_test, Y_train, Y_test, T_train, T_test = train_test_split(X, Y, T, random_state=42)

# 数据转换为Tensor
X_train = torch.tensor(X_train, dtype=torch.float32)
Y_train = torch.tensor(Y_train, dtype=torch.float32)
T_train = torch.tensor(T_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
Y_test = torch.tensor(Y_test, dtype=torch.float32)
T_test = torch.tensor(T_test, dtype=torch.float32)

# 数据加载
train_dataset = TensorDataset(X_train, Y_train, T_train)
test_dataset = TensorDataset(X_test, Y_test, T_test)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False)

# 定义DragonNet模型
class DragonNet(nn.Module):
    def __init__(self):
        super(DragonNet, self).__init__()
        self.shared = nn.Sequential(
            nn.Linear(183, 128),
            nn.ReLU(),
            nn.Linear(128, 64),
            nn.ReLU()
        )
        self.t_head = nn.Linear(64, 1)
        self.y0_head = nn.Linear(64, 1)
        self.y1_head = nn.Linear(64, 1)

    def forward(self, x):
        shared_rep = self.shared(x)
        t_pred = torch.sigmoid(self.t_head(shared_rep))
        y0_pred = self.y0_head(shared_rep)
        y1_pred = self.y1_head(shared_rep)
        return t_pred, y0_pred, y1_pred

# 训练函数
def train_model(model, train_loader, criterion_t, criterion_y, optimizer, num_epochs=50):
    model.train()
    for epoch in range(num_epochs):
        running_loss = 0.0
        for i, (inputs, y_true, t_true) in enumerate(train_loader):
            optimizer.zero_grad()
            t_pred, y0_pred, y1_pred = model(inputs)

            # 根据干预状态选择相应的头
            y_pred = t_true * y1_pred + (1 - t_true) * y0_pred

            # 计算损失
            loss_t = criterion_t(t_pred.view(-1), t_true)
            loss_y = criterion_y(y_pred.view(-1), y_true)
            loss = loss_t + loss_y

            # 反向传播和优化
            loss.backward()
            optimizer.step()
            running_loss += loss.item()

        print(f'Epoch {epoch + 1}/{num_epochs}, Loss: {running_loss / len(train_loader):.4f}')

# 损失函数和优化器
model = DragonNet()
criterion_t = nn.BCELoss()  # 用于处理二元分类任务的二进制交叉熵损失
criterion_y = nn.MSELoss()  # 用于处理回归任务的均方误差损失
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 训练模型
train_model(model, train_loader, criterion_t, criterion_y, optimizer, num_epochs=50)

# 评估模型
model.eval()
with torch.no_grad():
    running_loss = 0.0
    for inputs, y_true, t_true in test_loader:
        t_pred, y0_pred, y1_pred = model(inputs)
        y_pred = t_true * y1_pred + (1 - t_true) * y0_pred
        loss_t = criterion_t(t_pred.view(-1), t_true)
        loss_y = criterion_y(y_pred.view(-1), y_true)
        loss = loss_t + loss_y
        running_loss += loss.item()
    print(f'Test Loss: {running_loss / len(test_loader):.4f}')

# 使用模型进行预测
model.eval()
with torch.no_grad():
    for inputs in test_loader:
        inputs = inputs[0]  # 只需要输入特征
        t_pred, y0_pred, y1_pred = model(inputs)
        print(f'Predicted T: {t_pred}, Predicted Y0: {y0_pred}, Predicted Y1: {y1_pred}')

支付宝捐赠

微信捐赠