匹配方法的思路十分简单，它的基本原理就是找到可观测变量相同的情况下接受处置的个体和未被接受处置的个体，通过对比他们之间的差异从而计算处置效应。描述起来十分通俗易懂，但是实际操作的时候，它会有一些方法，接下来我们来看看这一章的内容。
匹配方法的理解
如果处置组和控制组的个体是随机分配的，那么它的估计应该是不存在差异的。换言之就是处置状态不受到可观测变量和不可观测变量的混淆影响。这里我们简单举例一个场景，假设个体的健康结果可以表示为年龄$Age$和情绪$e$以及服药效果$r$的线性关系。
$$
Y_{i}=D_{i} \times Y_{i}(1)-(1-D_{i}) \times Y_{i}(0)=\alpha+r_{i}D_{i}-bAge_{i}+e_{i}
$$
这个时候如果我们是随机的从全部数据中抽取实验组和控制组，通过观测处置和不处置的效果是可以很容易得到一个平均处置效果的估计。
在实际的应用中，面对的大多数情况往往的不到随机分配的数据，仅仅只有观测结果。观测结果又是个体选择的结果，与观测特征往往相关。例如上面的例子中，我们有30岁组合50岁组，50岁组的服药概率往往是大于30岁组。那么这样的例子求出来的处置效果是会存在一定的偏差的。
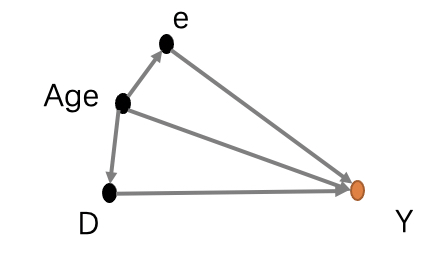
如上图，咱们将这个归因的路线图画出来，发现有一个混淆路径age，之前咱们讲过如何截断混淆路径呢？当然是将控制age这个变量，将归因路径图变成如下的形式。
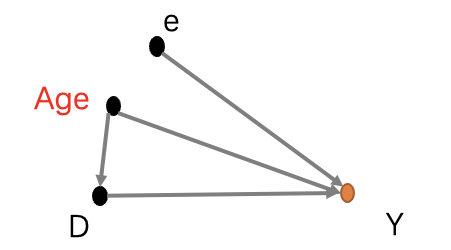
也就是说我们要将30岁的接受处置和为接受处置的一起分析，将50岁的接受处置和未接受处置一起分析就好啦。这样我们就能分别得出对于30岁组和50岁组不同的ATT等处置效应啦。说起来十分简单，但是实际工作中，如果我们想要估计这样的数据也是不容易的，所以应该将事情讲清楚以后构造可以构造这样的实验环境。
匹配方法的假设条件
老规矩，我们还是要讨论下匹配方法需要满足什么假设呢？
$$
Y_{i}(0),Y_{i}(1) \perp D_{i} | X_{i}
$$
也就是说当观测变量$X=x$的时候，接受处置与否是随机分配的，不会因为潜在的结果好坏决定是否接受处置。
共同支撑域条件
共同支撑域条件的意思是当给定可观测变量的时候，个体接受处置的概率大于0小于1，也就是不能一边倒的只有处置或者非处置的数据。
直接匹配法
本节我们来介绍匹配的一些方法，最简单的就是根据可观测数据直接进行特征的直接匹配，例如上面我们讲到的例子，将30岁和50组直接分组进行分析。这种方法比较直接我们就不做过多的讲解。
倾向性评分
直接匹配在我们的实际应用中并不常见，如果你有幸遇到，那么就只能恭喜你了啊。我们经常面对的可观测变量都是好几维甚至是好几十维度，这样就不能直接用直接匹配方法，所以这就引入了倾向性评分方法。倾向性评分的原理是通过函数关系将多维度的观测特征变成一维度的倾向性得分，再根据得分进行匹配。倾向性评分的可观测特征$X=x_{i}$的个体接受处置概率如下
$$
Ps(X=x_{i})=P(D_{i}=1|X_{i}=x)
$$
那么独立假设就成了
$$
Y_{i}(0),Y_{i}(1) \perp D_{i} | Ps(x)
$$
这是Rosenbaum and Rubin证明的。也就是说当处置组和控制组如果倾向性得分相同，他们的可观测特征分布没有差异。
倾向性得分的步骤
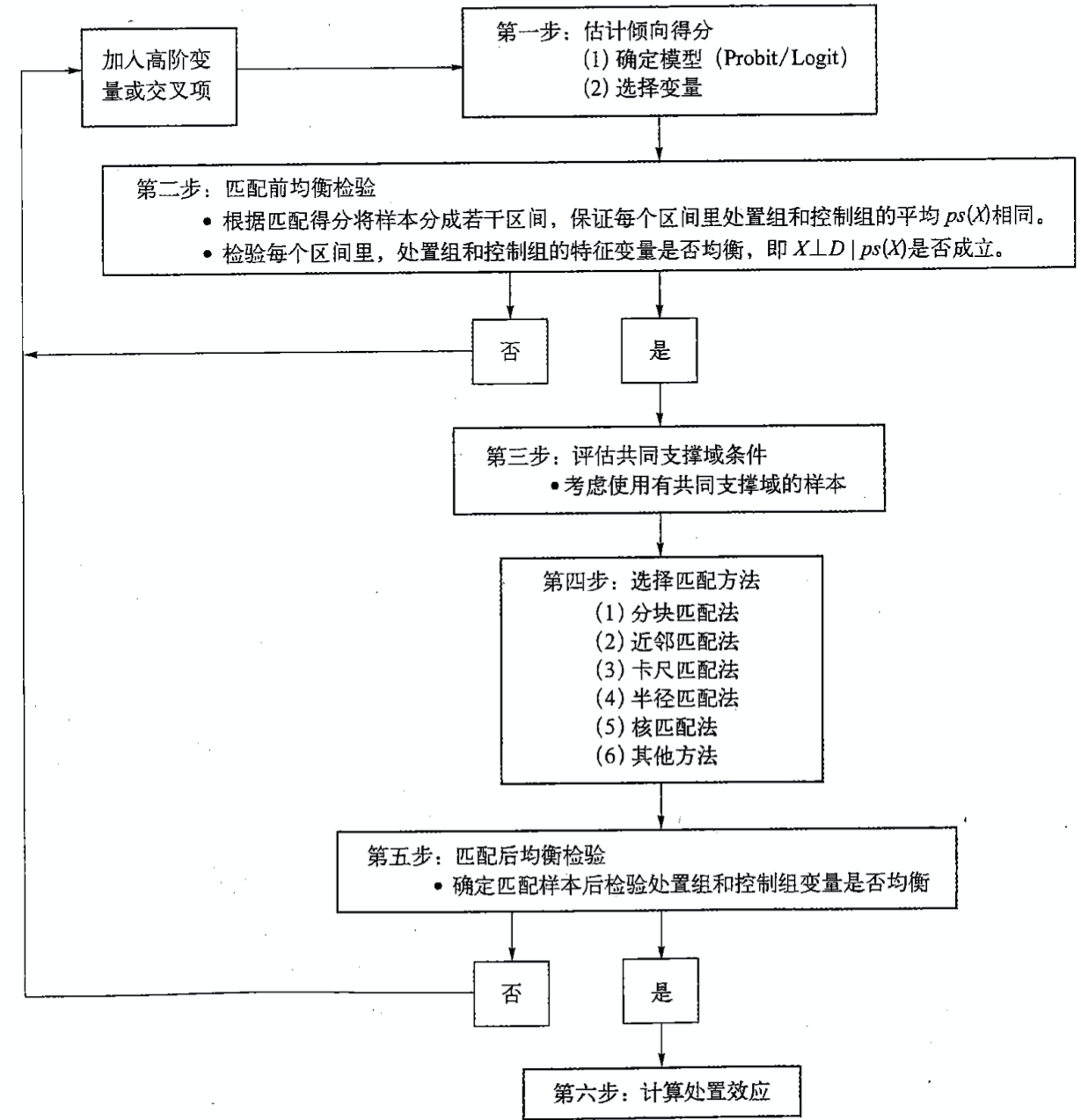
上面的步骤描述比较清楚，那么我们主要来说说选择匹配的方法
第一步的构建倾向性得分的模型的标签是是否被干预。
分块匹配法
分块匹配法是将倾向性区间切分为Q份，让每个区间的处置组和控制组的平均倾向性得分和可观测特征都达到均衡，然后通过每个区间的处置组和控制组结果的差异计算处置效果。
$$
ATT(q)=Y_{1}^{treatment}-Y_{0}^{control}
$$
最后总的ATT
$$
ATT=\sum_{q=1}^{Q} ATT(q) \frac{N_{q}^{treatment}}{N^{treatment}}
$$
$N_{q}^{treatment}$表示当前区间q的样本的数量。
近邻匹配法
这个比较好理解，就是对处置组中的样本选择控制组中倾向性得分比较近的作为其匹配样本。
近邻匹配法的缺点是存在处置组中的样本的倾向性得分和最近控制的倾向性得分相差较大
卡尺匹配法
卡尺匹配法只是在近邻匹配法的基础上加上一个阈值并称为卡尺而已。
匹配后均衡检测
我们匹配完以后需要检验匹配后的处置组和控制组的特征是否均衡，如果仍然存在较大差异就没有达到我们的预期。一般会使用如下的方法。
标准化偏差
匹配之前
$$
SB^{before}_{i}=100 \frac{\overline{X_{i,treatment}^{before}}-\overline{X_{i,control}^{before}}}{\sqrt{0.5Var(X_{i,treatment}^{before})}+Var(X_{i,control}^{before})}
$$
$\overline{X_{i,treatment}^{before}}$表示处置组的特征$X_{i}$在匹配前的均值，这里的匹配前的含义是没有经历匹配方法的情况下， 只通过观察T的值区分的实验组和对照组。其他变量可以通过符号能够推断其物理含义。
$$
SB^{after}_{i}=100 \frac{\overline{X_{i,treatment}^{after}}-\overline{X_{i,control}^{after}}}{\sqrt{0.5Var(X_{i,treatment}^{after})}+Var(X_{i,control}^{after})}
$$
上公式指的是处置后的标准化偏差。
偏差下降度的定义为
$$
BR_{i}=1-\frac{SB^{after}_{i}}{SB^{before}_{i}}
$$
当$SB^{after}_{i}<20$可以认为标准化偏差是可以接受的。
这里介绍一下这个检测， 因果推断的核心假设是处置动作独立于样本选择，这里通过PSM选取的样本也期望这两个分布尽可能的近，来印证处置动作是独立触发的，从而模拟RCT的结果。
t值检验
这个方法就是使用t统计值直接检验处置组和控制组的每个特征X在匹配后的均值是否存在显著差异。
F值检验
仅仅将t统计值改成F值而已。
已干预条件下的因果推断
我们知道实际的工作中，我们经常需要对已经实施的策略就行效果评估，这种已经干预下的因果效应叫做ETT(effect of treatment on the treated)
原始的计算处置效应的公式
$$
ETT = E[Y_{1}-Y_{0}|X=1] = E[Y_{1}|X=1] -E[Y_{0}|X=1] \tag{3.1}
$$
这里X=1以后，$Y_{0}$就是一个反事实的事件，其含义是说不处置的情况下Y的取值。这个时候如果我们能够找到变量集合Z相对于X和Y满足后门准则，则有以下的公式成立
$$\begin{gather}P(Y_{x}=y|X=x')=\sum_{z} P(Y_{x}=y|X=x',Z=z)P(Z=z|X=x')\\
=\sum_{z} P(Y_{x}=y|X=x,Z=z)P(Y_{x}=y|X=x',Z=z)P(Z=z|X=x') \\
=\sum_{z} P(Y=y|X=x,Z=z)P(Y_{x}=y|X=x',Z=z)P(Z=z|X=x') \tag{3.2}\end{gather}$$
第二个等号因果序列Z满足(X,Y)的后门路径，此时的X和反事实$Y_{x}$是关于Z条件独立的，所以可以将X=x'替换成X=x。第三个等号后面的含义是利用反事实的一致性法则，在X=x的时候可以将$Y_{x}$替换成Y。
对于公式1.1可以完整改写
$$\begin{gather}ETT= E[Y_{1}-Y_{0}|X=1] \\
=P[Y_{1}=1|X=1]-P[Y_{0}=1|X=1] \\
=P[Y|X=1]-]-\sum_{z}P(Y=1|X=0,Z=z)P(Z=z|X=1) \tag{3.2}\end{gather}$$
这个时候如果你找到一个后门变量z，也可以通过如下的方式进行计算反事实。
$$\begin{gathered}P(Y_{x}=y)=P(Y_{x}=y|X=x)P(X=x)+P(Y_{x}=y|X=x')P(X=x')\\
=P(Y=y|X=x)P(X=x)+P(Y_{x}=y|X=x')P(X=x')\\
=P(Y=y,X=x)+P(Y_{x}=y|X=x')P(X=x')\end{gathered}$$
进而可以推知
$$\begin{gathered}P(Y_{x}=y|X=x')=\frac{P(Y_{x}=y)-P(Y=y,X=x)}{P(X=x')} \\
=\frac{P(Y=y|do(X=x))-P(Y=y,X=x)}{P(X=x')}\end{gathered}$$
这样就可以不用找到后面变量z就可以计算反事实数据。
一个简单的理解
原始的因果推断需要满足的条件是
$$
Y(1),Y(0) \perp D \tag{1.1}
$$
D是处置动作，Y(1)表示处置动作为1下的结果，Y(0)表示处置动作为0下的结果.
这里存在反事实的问题，所以希望通过倾向性得分的方式获得以下的条件成立
$$
Y(1),Y(0) \perp D |PS(X) \tag{1.2}
$$
PS表示计算倾向性得分的模型，X表示影响结果的协变量，也就是在对齐倾向性得分的情况下，达成公式1.1的条件。
这样通过PS(X)就能对现有的实验组和对照组进行一个打分（倾向性得分）， 这里PS(X)打分的目的是找到实验组和对照组环境变量基本一致的样本。【PS(X)实际上是一致性的的一个打分，进一步的例子就是我们有负载=0.5的时候调控过，也有负载实际没有到0.5，背景变量很相近，但是没调控的例子，支撑逻辑上是可以挖掘出来的】
给每一个实验组和对照组的样本打上的倾向性得分以后，会有一个匹配策略。 主要干的事情就是在实验组里样本的倾向性得分0.8的，在对照组里也希望能找到离0.8很近的样本作为对照组，从而构建一个新的实验组和对照组。
最后在新的实验组和对照组进行 影响面的计算