接着上文说假如 $Y=\alpha + \beta X+e$ 以及$E[e|X]=0$是可以满足的，而且我们有全集的数据，那么我们使用最小二乘法得到的系数$\alpha \beta$是不存在方差的。但是如果我们只有样本数据，那么得到的估计系数$(\vec{\alpha},\vec{\beta})$ 是$(\alpha,\beta)$无偏估计。真实的环境中我们只是使用样本数据，得到的估计值和真实值有一定的差异，因此我们需要对估计的系数可能的误差范围进行估计。估计的系数的标准差称为系数标准差。造成样本估计值存在的误差的原因是干扰项e的存在。实际环境中我们经常遇到的4种干扰项分别是。

1. 同方差
2. 异方差
3. 自相关
4. 集群相关

同方差

在带干扰项的最小二乘法的推导中，回归系数的协方差矩阵$Var(\beta)$的表达式为

$$Var(\beta)=(X'X)^{-1}X'E[ee']X(X'X)^{-1} \tag{1.1}$$

上篇博客中回归系数假设4是如下描述的。

E(ee')=\begin{equation} \left( \begin{array}{ccc} \sigma_{1}^{2} & \sigma_{12} & \sigma_{1n}\\ \sigma_{21} & \sigma_{2}^{2} & \sigma_{2n}\\ \sigma_{n1} & \sigma_{n2} & \sigma_{n}^{2}\\ \end{array} \right) \end{equation}

对于E(ee’)主对角线的项$\sigma_{i}^{2}$表示第i个观测点干扰项的方差，对角线外的$\sigma_{ij}$表示第i个观测点和第j个观测点干扰项的协方差。
综上所述，干扰项的协方差矩阵是决定估计系数的方差的关键因素。
同方差指的是，每个观测点方差大小相同。在实际应用中，同方差假设也伴有不相关假设。也就是当i!=j的时候，方差值均为0.这是一个比较特殊的情况，现实中不是特别容易出现。例如，我们研究教育对收入的影响，如果随机抽取100名工人，同方差假设就认为，影响每个工人的收入干扰因素是不相关且方差大小一致的。
同方差矩阵的表示形式如下。

E(ee')=\begin{equation} \left( \begin{array}{ccc} \sigma^{2} & 0 & 0\\ 0 & \sigma^{2} & 0\\ 0 & 0 & \sigma^{2}\\ \end{array} \right) \end{equation}

可以知道同方差矩阵中，那么同方差属性的数据，回归出来的拟合效果是怎么样的呢？

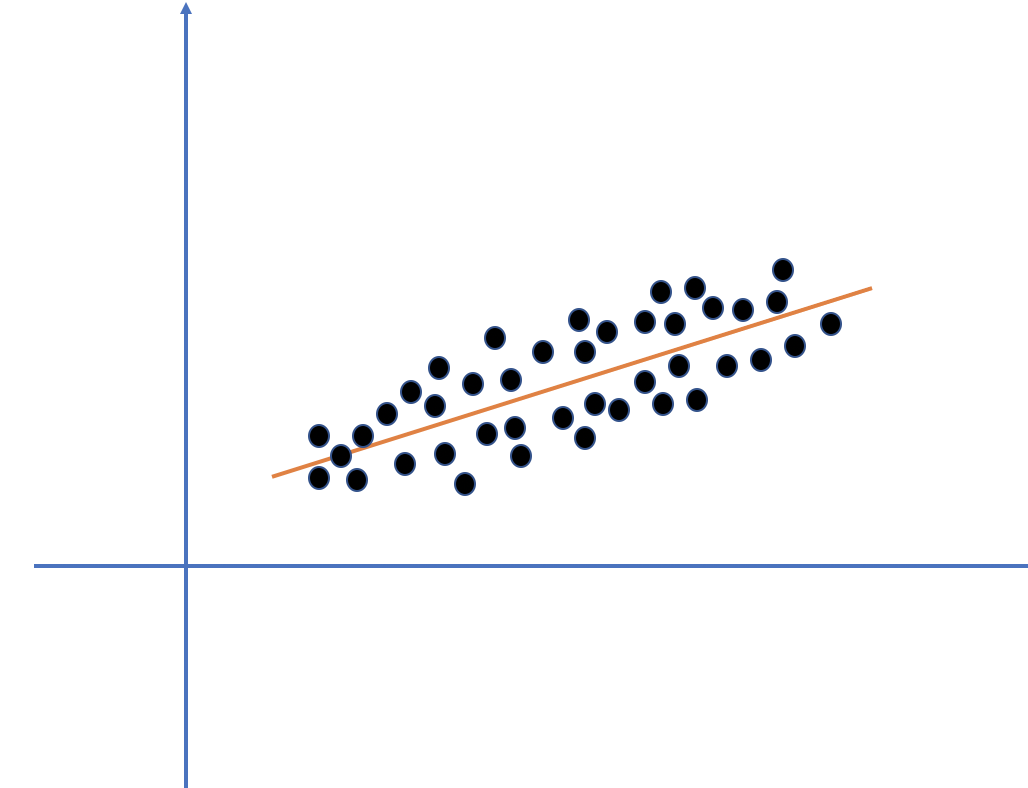
可以看见，观测点均匀落在拟合曲线的周边。在实际的生活中，同方差的例子十分的少，比较常见的反而是异方差和自相关。

实际生产中经常使用如下的方法处理异方差和自相关问题

1. 先将模型进行转换，让干扰项满足同方差在用OLS进行回归，这种方法叫做广义最小二乘法。听起来十分简单，但是这个方法的难点是模型转换需要预知干扰项的协方差矩阵形式，这一点通常十分复杂
2. 不转换模型，直接用OLS进行回归，并计算异方差和自相关条件下的OLS估计系数的方差。异方差和自相关知识造成OLS估计值的方差较大，不影响无偏性。可见这种方法就是估计出来的系数偏差会比较大。

异方差

异方差是指每个观测点的干扰项的方差不相等，但是不同观测点干扰项是不相关的就是有$Cov(e_{i}m e_{j})=0$.

E(ee')=\begin{equation} \left( \begin{array}{ccc} w_{1} & 0 & 0\\ 0 & w_{2} & 0\\ 0 & 0 & w_{3}\\ \end{array} \right) \end{equation}

那么异方差下的干扰项分布的曲线是什么样子呢？

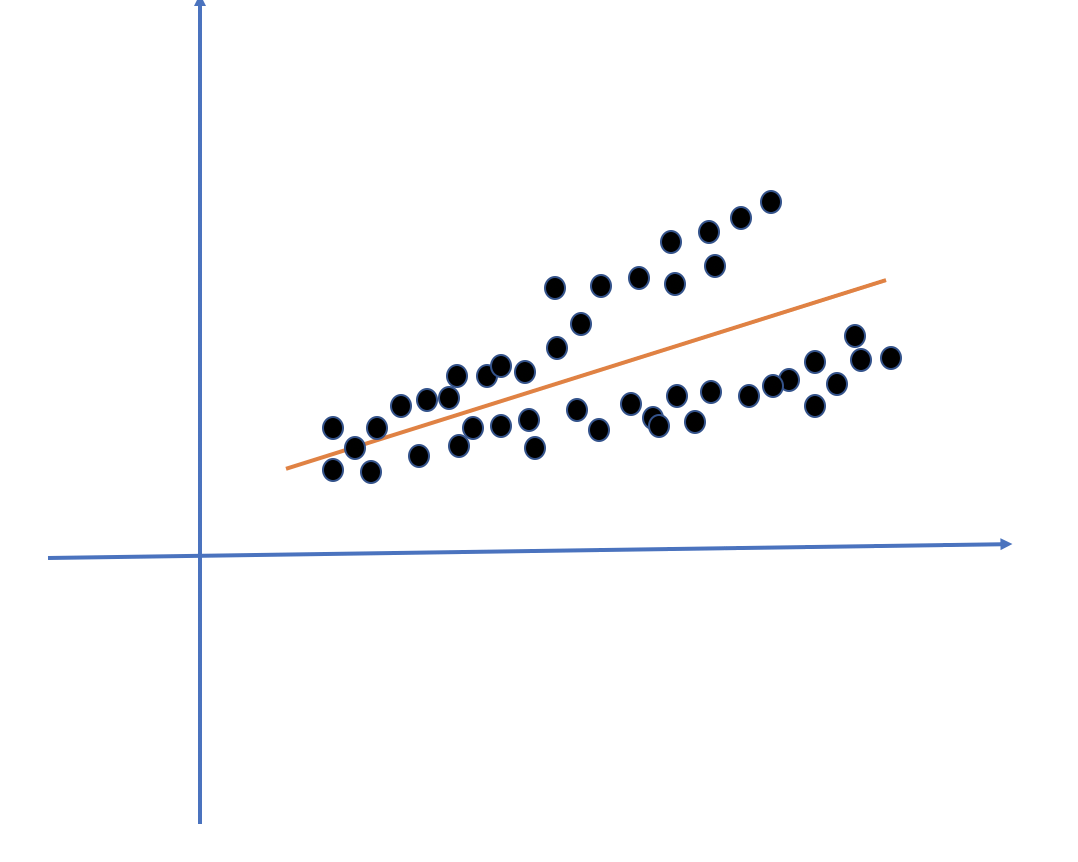
可以看到当X值越大的时候，干扰项值的分布越分散。但是重复抽样下，较大的真误差和较大的负误差会相互抵消，因此异方差情况下样本的估计值仍然是无偏的。虽然是无偏的但是当X值越大的时候，Y值的干扰越大。这里需要说明一下异方差和同方差产生的误差是不太一样。

自相关

通常我们将异方差和自相关产生的干扰一起考虑，就是如下这种形态。

E(ee')=\begin{equation} \left( \begin{array}{ccc} \sigma_{1}^{2} & \sigma_{12} & \sigma_{1n}\\ \sigma_{21} & \sigma_{2}^{2} & \sigma_{2n}\\ \sigma_{n1} & \sigma_{n2} & \sigma_{n}^{2}\\ \end{array} \right) \end{equation}

自相关和异方差意味着每个观测点的干扰项是从相关并且不相同的分布从产生的。自相关产生的原因是十分复杂的，那么如果自相关和异方差产生的回归效果又是如何的呢？

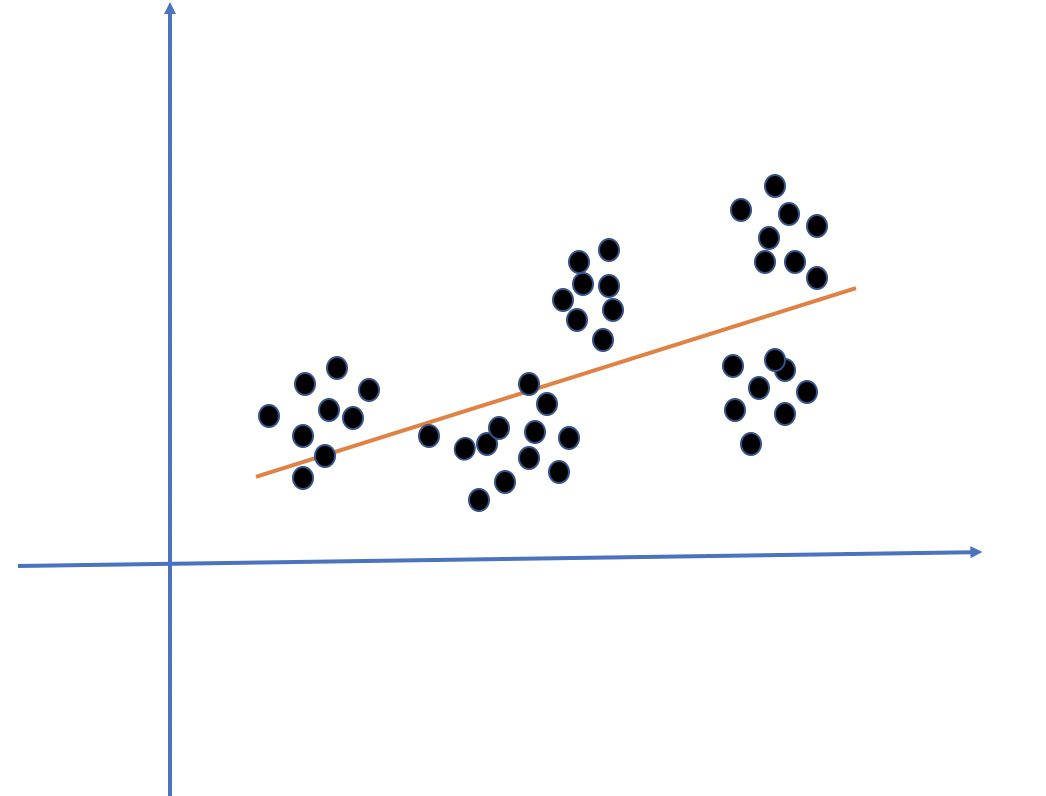
如上图是自相关的情况下的干扰项的分布情况，我们可以观测，当第一个干扰项偏离关系线为正时，接下来几个干扰项偏离值也为正，同样的偏离为负也是类似。

如果要解决如上的问题，可就要用到广义的最小二乘法，希望大家能够了解一下。

集群相关

集群相关指的是同一个集群下的干扰项是相关的，但是不同集群的干扰项是不相关的。一个例子就是一个企业同年份是一个集群，而不同年份是不同集群。这里我们就不过多解释啦。