总效应和直接效应
之前分析的所有的关于因果效应$P(y|\bar{x})$分析的是单个变量和结果变量的总效应（total effect）.许多情况下结果不足以满足应用目标的需求，这个是就要引入直接效应，所谓的直接效应意味着量化一种不受模型中其他变量影响的效应。更准确的说，当分析中所有其他变量都保存不变，Y对X变化的敏感度就是直接效应。
咱们先通过一个例子来引出今天的话题。大家一直怀疑避孕药会在女性的身体形成血栓，同时还能降低怀孕率。怀孕又对血栓的形成具有负面的作用（怀孕导致血栓的形成。）所以如果我们想要探索避孕药和血栓形成的关系仅仅通过控制中间变量怀孕是不足够看清楚关系的。必须要对那些使用避孕药之前就怀孕的，以及通过非药物手段进行避孕的女性进行研究。详细的说是通过条件化中间变量（怀孕），即使避孕药和血栓形成没有直接效应，也可能产生伪相关。(X<-Z<-U->Y)。X和Y没有直接效应，如果保持Z不变X和Y不存在关联。但是如果以Z为条件，就会通过U(未观察到的变量)产生伪相关，认为X和Y有直接效用。
直接效应
现实生活中控制所有变量都不变做实验是不太可能的事情。下面给出完整定义。
X对Y的直接效应使用符号表示为$P(y|\hat{x},\hat{s}_{XY})$,其中$S_{XY}$表示系统中除了X和Y之外的所有内生变量的集合。
事实上没有必要控制所有变量不变，只需要将Y的父变量不包括X的部分保持不变就行啦。所以直接效应的如下定义:
X对Y的直接效应表示为$P(y|\hat{x},\hat{pa}_{Y/X})$,其中$\hat{pa}_{Y/X}$表示除去X以外的Y的父节点的集合。
自然直接效应
自然直接效应想要探索的是将我们把变量中的X的值从x替换成x'最终引发的效果。
$$
DE_{x,x'}(Y)=E[(Y(x',Z(x)))-E(Y(x))] \tag{1.0}
$$
其中Z是除了X外所有父节点的集合，$(Y(x',Z(x)))$表示将X设置为x',并且将Z设置为X=x得到的值时Y的值。这里就表达了将变量从x'设置到x以后Y的自然直接效应。进一步化简为如下形式。
$$
DE_{x,x'}(Y)=\sum_{z}[E(Y|do(x',z))-E(Y|do(x|z))]P(z|do(x)) \tag{1.1}
$$
这个公式的理解十分简单，就是自然直接效应是受控直接效应的加权求和。用P(z|do(x))表示其权重.公式1.1中P(z|do(x))可以进一步化简
$$
P(z|do(x))=\sum_{t}P(z|x,pa_{x}=t)P(pa_{x}=t)
$$
间接效应
可以发现一个问题，通过使用do(x)操作不可能做到禁止X到Y的直接链接，而使得X仅仅通过其他的间接路径影响Y。
这里使用x到x'的间接效应定义为：通过保持变量X的值不变，并使得变量Z的值设置为等效于X变化为x'所引起的变化值，说得到的Y的预期变化。
$$
IE_{x,x'}(Y)=E[(Y(x,Z(x')))-E(Y(x))] \tag{2.0}
$$
一个变化的总效应等于直接效应和间接效应的差值
$$
TE_{x,x'}(Y)=DE_{x,x'}(Y)+IE_{x,x'}(Y)
$$
在无混杂中间变量的简单情况，可以通过下面两个回归方程来估算自然直接效应和自然间接效应，这两个方程称为中介公式
$$\begin{gathered}DE_{x,x'}(Y)=\sum_{z}[E(Y|x',z)-E(Y|x,z)]P(z|x) \\
IE_{x,x'}(Y)=\sum_{z}E(Y|x,z)[P(z|x')-P(z|x)]\end{gathered}$$
另一个视角看中介效应
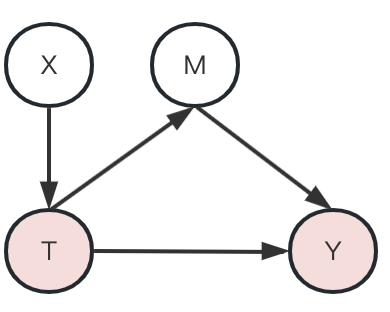
上图中的M就是中介变量，X可以称为预前协变量。
因果中介效用
这里介绍如何识别T到Y的因果效应，首先$M_{i}(T_{i}=t)$表示当$T_{i}=t$的情况下M的值，可以将潜在的结果表示为一个中介变量和处理变量的函数，对应一个结果变量$Y_{i}(T_{i}=t,M_{i}=m)$，表示当单位i的处理变量取值为t的时候，中介变量为m的潜在结果。
对于二元处理变量$T \in [0,1]$， 单位i的因果效应$\sigma(t)$是一个处理变量的函数。
$$
\sigma_{i}(t)=Y_{i}(T=t, M_{i}=1)-Y_{i}(T=t, M_{i}=0) \tag{1.1}
$$
从上面的公式能够看出来，因果中介效应代表处理变量通过影响中介变量对结果变量的因果效应，这里会枚举T=1和T=0计算，最终将所有的$\sigma_{i}(t)$求平均就是中介效用。因果中介效应$\sigma_{i}(t)$也被称为间接效应。其实因果中介效应其实也包含一些假设，潜在的结果变量仅仅受到了处理变量和中介变量的影响。
通过上面的介绍，也比较容易推导出平均因果中介效应
$$\begin{gather}\sigma(t)= E[\sigma_{i}(t)] \\
=E[Y_{i}(T=t, M_{i}=1)-Y_{i}(T=t, M_{i}=0)] \tag{1.1}\end{gather}$$
总因果效应
还是假设二元处理变量$T \in [0,1]$，单位i的总因果效应为$\tau$ 定义如下
$$
\tau_{i}=Y_{i}(T=1, M_{i}(1))-Y_{i}(T=1, M_{i}(0)) \tag{2.1}
$$
下面公式表示自然直接效应
$$
\zeta(1-t)=Y_{i}(T=1-t,M_{i})-Y_{i}(T=0,M_{i}) \tag{2.2}
$$
而总因果效应就有了如下的表达
$$
\tau_{i}=\sigma_{i}(t)+\zeta(1-t) \tag{2.3}
$$
看看我们如何理解上面这些关系，首先$\zeta(t)$是一个处理变量t的函数。可以理解为处理变量不通过中介变量干预结果变量，这是直接对结果变量产生影响，所以这里固定了$M_{i}(t)$，改变处理变量对结果变量的影响。而公式2.3表示总因果效应是因果中介效应在处理变量t时的取值，与直接效应在处理变量为1-t的取值之和。
一个现实的例子
例如在一个招聘系统中，如果消除了性别歧视，所有的申请者都是公平对待，那么策略指定者可能关心性别的比例构成，这一个比例将由性别对雇佣关系的间接效应决定。也就是通过教育背景、工作能力的与性别有关的因素决定。