基于值的深度强化算法

上篇文章咱们介绍了Qlearning，这个时候正好我们就机会来详细看看DQN的学习方式，同样的之前的章节中我们介绍了DQN的原理，但是没有一个特别好的例子，本节咱们就来补上这一块。

DQN的使用场景就是我们发现使用Qlearning能够在离散状态空间下解决任何强化学习问题，但是如果状态空间是无限的或者是连续的怎么办呢？ DQN的核心思路是将原有的离散状态空间表示为一个函数f。

$$f(s,a)=Q(s,a)$$

这也就是知道了，我们思想通过学习的方式构建状态动作空间和值函数的映射关系，思路简单粗暴。这个时候又浮现出另一个问题，既然是通过训练，那么标签是什么？这个就要感谢我们之前学习了Q-Learning 的知识。我们称为经验池。怎么来构造这个标签呢？实际上是通过Q-Learning使用reward来构造标签。这里就引入了经验池的概念。

经验池

已知一个状态$s_{t}$ ，通过 Q网络 得到各种动作的Q值，然后用$\sigma$贪婪策略 选择动作$a_{t}$ （$\sigma$贪婪策略是为了保证一定的探索，大概率会选择Q值最大的那个动作），然后将 $a_{t}$ 输入到环境中(真实的强化环境)，得到 $s_{t+1}$ 和 $r_{t+1}$ ，这样就得到一个experience: $s_{t}, a_{t}, s_{t+1}, r_{t+1}$ ，然后将experience放入经验池中。构建好这个大的经验池，后续我们就是通过随机的抽取学习就好了。
这里需要回答一个问题是，为什么要使用经验池。
神经网络进行训练时，假设样本是独立同分布的。而通过强化学习采集到的数据之间存在着关联性，利用这些数据进行顺序训练，神经网络当然不稳定。
经验回放通过随机抽取，可以打破数据间的关联。

DQN

拿到了上面的经验池，怎么来使用呢？我们先来看下面这个网络结构，Nature DQN使用了两个Q网络，一个当前Q网络𝑄用来选择动作，更新模型参数，另一个目标Q网络𝑄′用于计算目标Q值。目标Q网络的网络参数不需要迭代更新，而是每隔一段时间从当前Q网络𝑄复制过来，即延时更新，这样可以减少目标Q值和当前的Q值相关性。然后解释一下这个网络是如何学习和更新的.

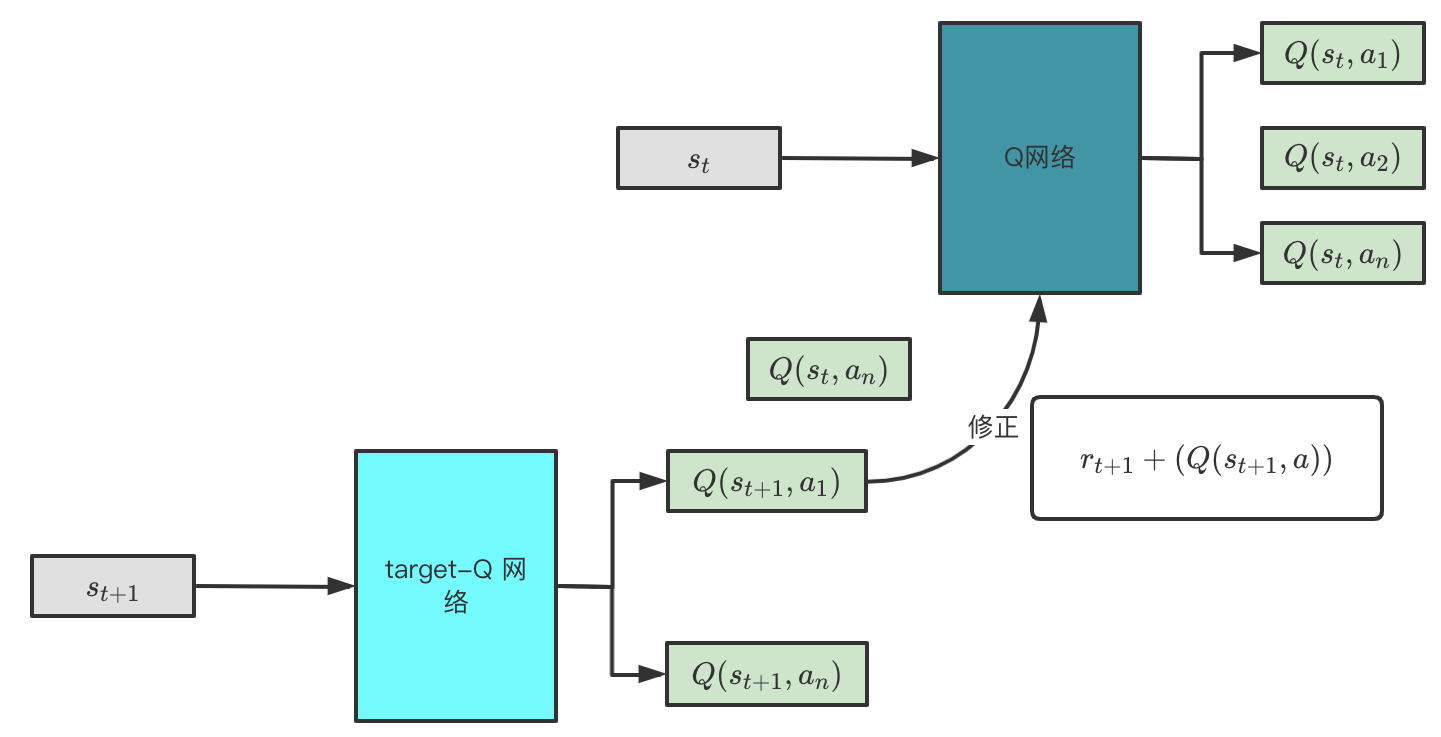
首先根据$s_{t}$和$a_{t}$通过Q网络计算出$Q(s_{t},a_{t})$的值，这里假设$a_{t}=a_{1}$，然后将下一状态$s_{t+1}$输入到target-Q网络，得到不同动作的Q值，然后选择最大的Q值确定动作$a_{2}$，然后以$Q(s_{t}, a_{1})$作为预测值，而$r_{t+1}+Q(s_{t+1},a_{2})$作为实际值进行反向传播，这里和监督学习就一样啦。过一段时间后，将Q网络中的参数硬拷贝到Target Q网络中。这样我们就完成一个DQN的学习，整个过程还是挺复杂的。

import numpy as np
import random
from collections import deque
import torch
import torch.nn as nn
import torch.optim as optim

class DQN(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(state_dim, 128)
        self.fc2 = nn.Linear(128, 128)
        self.fc3 = nn.Linear(128, action_dim)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        return self.fc3(x)

class DQNAgent:
    def __init__(self, state_dim, action_dim, lr=0.001, gamma=0.99, epsilon=1.0, epsilon_min=0.01, epsilon_decay=0.995, target_update_freq=100):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.gamma = gamma
        self.epsilon = epsilon
        self.epsilon_min = epsilon_min
        self.epsilon_decay = epsilon_decay
        self.target_update_freq = target_update_freq
        self.steps = 0

        # 主网络
        self.model = DQN(state_dim, action_dim)
        self.optimizer = optim.Adam(self.model.parameters(), lr=lr)
        self.criterion = nn.MSELoss()

        # 目标网络
        self.target_model = DQN(state_dim, action_dim)
        self.target_model.load_state_dict(self.model.state_dict())

        self.replay_buffer = deque(maxlen=10000)

    def select_action(self, state):
        if random.random() < self.epsilon:
            return random.randint(0, self.action_dim - 1)  # 随机动作
        else:
            with torch.no_grad():
                state_tensor = torch.FloatTensor(state).unsqueeze(0)
                q_values = self.model(state_tensor)
                return q_values.argmax().item()  # 选择 Q 值最大的动作

    def train(self, batch_size):
        if len(self.replay_buffer) < batch_size:
            return

        batch = random.sample(self.replay_buffer, batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)

        states = torch.FloatTensor(np.array(states))
        actions = torch.LongTensor(actions)
        rewards = torch.FloatTensor(rewards)
        next_states = torch.FloatTensor(np.array(next_states))
        dones = torch.FloatTensor(dones)

        # 计算当前 Q 值
        current_q = self.model(states).gather(1, actions.unsqueeze(-1))

        # 计算目标 Q 值
        with torch.no_grad():
            next_q = self.target_model(next_states).max(1)[0]
            target_q = rewards + (1 - dones) * self.gamma * next_q

        # 计算损失并更新主网络
        loss = self.criterion(current_q.squeeze(), target_q)
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        # 更新目标网络
        self.steps += 1
        if self.steps % self.target_update_freq == 0:
            self.target_model.load_state_dict(self.model.state_dict())

        # 衰减 ε
        self.epsilon = max(self.epsilon_min, self.epsilon * self.epsilon_decay)

    def save_experience(self, state, action, reward, next_state, done):
        self.replay_buffer.append((state, action, reward, next_state, done))

上文给出了DQN的python实现。通过和环境进行交互，获得缓冲池，然后进行训练。

过往的研究表明，使用非线性网络表示值函数时出现不稳定等问题。所以这里我们要使用两个网络来学习以保证稳定性。 基于这样的时候还有好几种类似的学习方式，本节就不一一介绍了，后续有精力咱们再来整理一下这类神经网络的改进点都是什么。

DDQN

传统的Qlearning和DQN都存在一个问题就是值函数估计过大的问题，且动作空间越大，误差越大，这与算法本身采用Max动作造成的。如果这种过估计是均匀的，那么不会影响到我们的最优策略，但是实际中往往是非均匀分布的，所以会造成比较大的误差。
在传统的DQN中，求TD目标的时候，往往是选取一个动作$a^{*}$，满足如下表达式。

$$a^{*}=argmax\ Q(S_{t+1}, a; \theta_{t})$$

评估使用的是

$$Y^{DQN}=R_{t+1}+r*max\ Q(S_{t+1}, a; \theta_{t})$$

可见传统的DQN不管是选择action还是评估action都是采用的一套参数$\theta_{t}$.
而DDQN采用的是不同的值函数和评估函数，使用上文提到的DQN网络，使用主网络进行动作选择，使用另一个网络进行动作评估。算法流程如下。可以看出与原始的DQN唯一的不同就是。不再是直接在目标Q网络里面找各个动作中最大Q值，而是先在当前Q网络中先找出最大Q值对应的动作。然后利用这个选择出来的动作在目标网络里面去计算目标Q值。可以仔细看到下面的伪代码中对于y的定义的变化。

从上面的总结来看双Q网络的核心思想是将选择和评估分开。在双Q学习中有两套值函数，每次学习经历都随机放到其中一个值函数进行更新，这样就出现了两套参数$\theta$和$\theta'$，那么每次更新的时候，其中一组用来决定贪心策略，另一组用来确定值。ß