讲了很久的控制论,今天就来讲解一个控制论的真实使用场景,做算法的应该知道,我们经常需要花钱买一些流量或者是转化,这里涉及到几个问题, 钱不是无穷的,往往我们需要有一个预算需要管理, 如果管理预算能力较差,会导致系统的稳定性差,当遇到一些极端场景的时候,现金池很可能被抽干,当然这里涉及到预算分配和预算管理的内容,今天我们的重点是预算分配。
场景描述
假设预算分配如下,budgets = [100, 200, 100], 第一个小时有100元的预算,第二个小时有200元的预算。每个时刻也会产生一个花费数据,costs = [60, 250, 85.122]。那么我们期望通过调整每个小时的动态预算,控制整体的预算结果。
根据PID算法,会产生如下的预算转移。
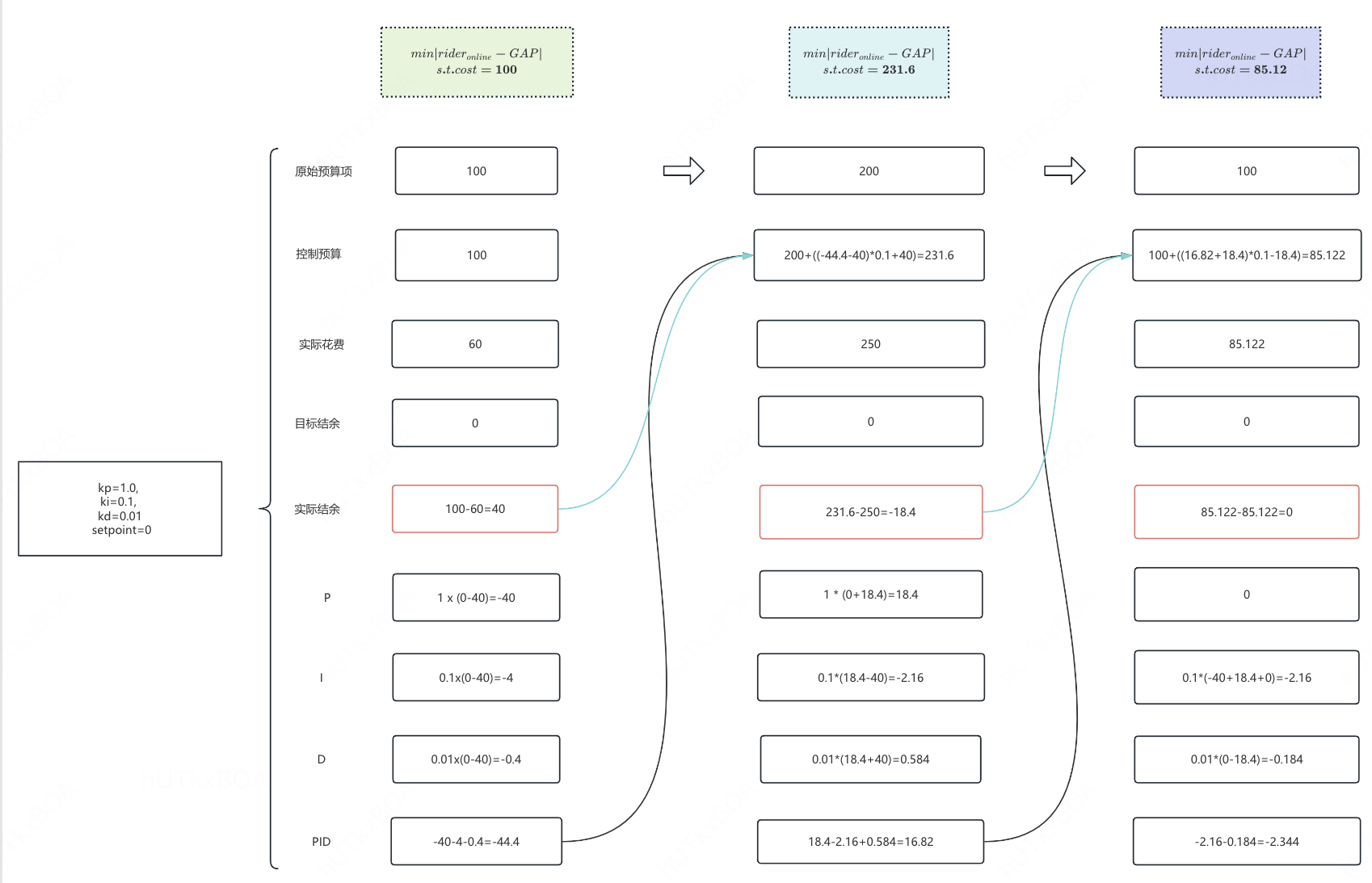
这里需要强调的是算法控制的目标是∣gap(预算,花费)∣, 所以第一个小时产生的gap是40,目标是将这个40在下一个时间片内进行消化掉,从而在外层能够保证一个整体的预算稳定在某个区间下。
PID
- 比例(Proportional, P)项:
- 这部分根据当前误差的大小直接调整控制量。
-
- 积分(Integral, I)项:
-
-
- 微分(Derivative, D)项:
-
-
这里再宏观温习一下PID算法,其中每一项所做的目标如上表所示。
代码
import time
import random
import numpy as np
class PIDController:
def __init__(self, kp, ki, kd, setpoint):
self.kp = kp # 比例增益
self.ki = ki # 积分增益
self.kd = kd # 微分增益
self.setpoint = setpoint # 设定值
self.error_sum = 0
self.last_error = 0
self.last_time = time.time()
def update(self, current_value):
"""
Updates the PID controller and returns the control signal.
"""
# current_time = time.time()
# dt = current_time - self.last_time
# self.last_time = current_time
dt = 1
error = self.setpoint - current_value
self.error_sum += error * dt
error_derivative = (error - self.last_error) / dt
self.last_error = error
control_signal = self.kp * error + self.ki * self.error_sum + self.kd * error_derivative
return control_signal
# Example usage
pid = PIDController(kp=1.0, ki=0.1, kd=0.01, setpoint=0)
# Simulate a system with a current value
budgets = [100, 200, 100]
costs = [60, 250, 85.122]
cnt = 0
budget_sum = 0
cost_sum = 0
current_loss = 0
while cnt <= 2:
budget = budgets[cnt] + current_loss
#cost = random.randint(int(budget * 0.5), int(budget * 1.5))
cost = costs[cnt]
current_loss = budget - cost
control_signal = pid.update(current_loss)
budget_sum += budget
cost_sum += cost
print(f"budget:{budget}, "
f"cost:{cost}, "
f"setpoint: {pid.setpoint}, "
f"current value: {current_loss},"
f"control signal: {control_signal}",
f"budget sum:{budget_sum}",
f"cost sum:{cost_sum}",
f"all budget:{np.sum(budgets)}"
)
# Update the current value based on the control signal
current_loss += (control_signal - current_loss) * 0.1
cnt += 1
上述代码的输出为
budget:100, cost:60, setpoint: 0, current value: 40,control signal: -44.4 budget sum:100 cost sum:60 all budget:400
budget:231.56, cost:250, setpoint: 0, current value: -18.439999999999998,control signal: 16.868399999999998 budget sum:331.56 cost sum:310 all budget:400
budget:85.09084, cost:85.122, setpoint: 0, current value: -0.031159999999999854,control signal: -2.3058124 budget sum:416.65084 cost sum:395.122 all budget:400
上面的代码模拟了预算控制的过程, 系统通过每次的误差影响下一次的预算分配,随着时间的推移持续优化这个误差,目标是将系统稳定在0附近,也就是预算多少就花多少。
当然这个算法也能进行一定程度的改进,例如你有未来一些预测信息, 可以引入到PID的计算过程, 进一步提升预算控制稳定性。