今天咱们再开始一个新的领域的内容,经典的三大范畴,推理论、决策论和控制论是其中一个比较容易被忽视的科学,但是在实际的业务中又有着经典的使用场景,当我们进行成本控制的时候,经常需要控制论中的一些经典知识,现在也抽时间开启这部分内容的学习。
控制论主要的研究对象是动态系统,所谓的动态系统是指状态随着时间变化的系统,其特点是系统的状态变量是时间得函数。
动态系统
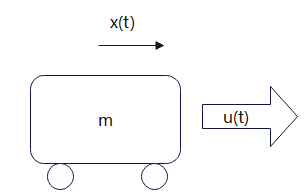
平面上有一个质量为m的小车,如果给小车施加一个外力u(t),就构成了一个动态的系统,小车位移了x(t)是此系统的状态变量,它是一个时间函数,随着时间t的变化的导数为dtd(x),这就是小车的速度。而速度随着时间的变化率为dt2d2x(t),代表小车的加速度,那么牛顿第二定律就得到如下的表达
u(t)=mdt2d2x(t)(1.1)
这就是一个动态系统,其中u(t)表示输入,x(t)表示系统的输出,公式1.1就是表达给定了系统的输入,将通过影响小车的速度和加速度最终影响系统的输出。
adt2d2x(t)+bdtdx(t)+c(t)x(t)=u(t)(1.2)
上面这个系统就是一个线性的时变系统,因为参数c(t)是随着时间变化的。
adt2d2x(t)+bdtdx(t)+sinx(t)=u(t)(1.3)
上面这个系统是非线性时不变系统,因为有非线性项sinx
把公式1.2的c(t)x(t)变成cx(t)就变成了线性的不变系统了。
控制系统
上面讲完了动态系统,接下来就是控制系统,控制系统是由控制器和动态系统组成,控制器会根据参考值r(t)决定控制量,然后给动态系统输入u(t),这种简单的方式称为开环控制。
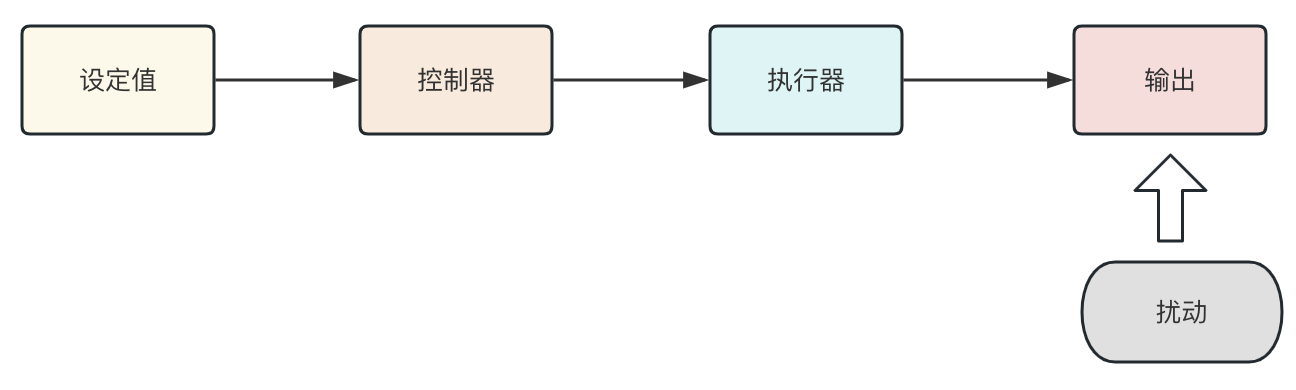
如下图所示,如果系统能够精准的获取系统的反馈值并将其反馈到输入端的参考值进行比较。那么就是一个闭环的控制系统。
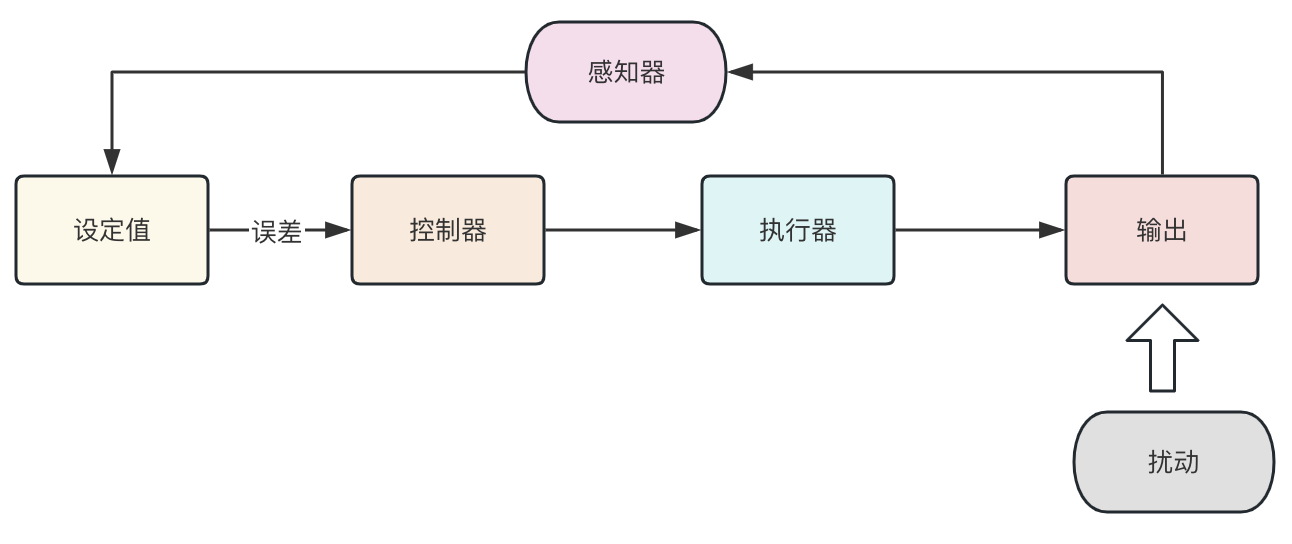
参考值和实际系统的输出差称为误差。综上所述,反馈是控制的基础, 动态是反馈控制的基础。
总而言之
接下来的章节中咱们就来介绍针对这套控制系统应该如何建模,在那些环节建模等问题。