FFM 模型采用引入特征域的方式增强了模型的特征交叉能力,但无论如何, FFM 只能做二阶的特征交叉,如果继续提高特征交叉的维度,会不可避免地产生 组合爆炸和计算复杂度过高的问题。那么就引入今天要说的新的模型趋势LR+GBDT
LR+GBDT
模型的结构如图1所示。
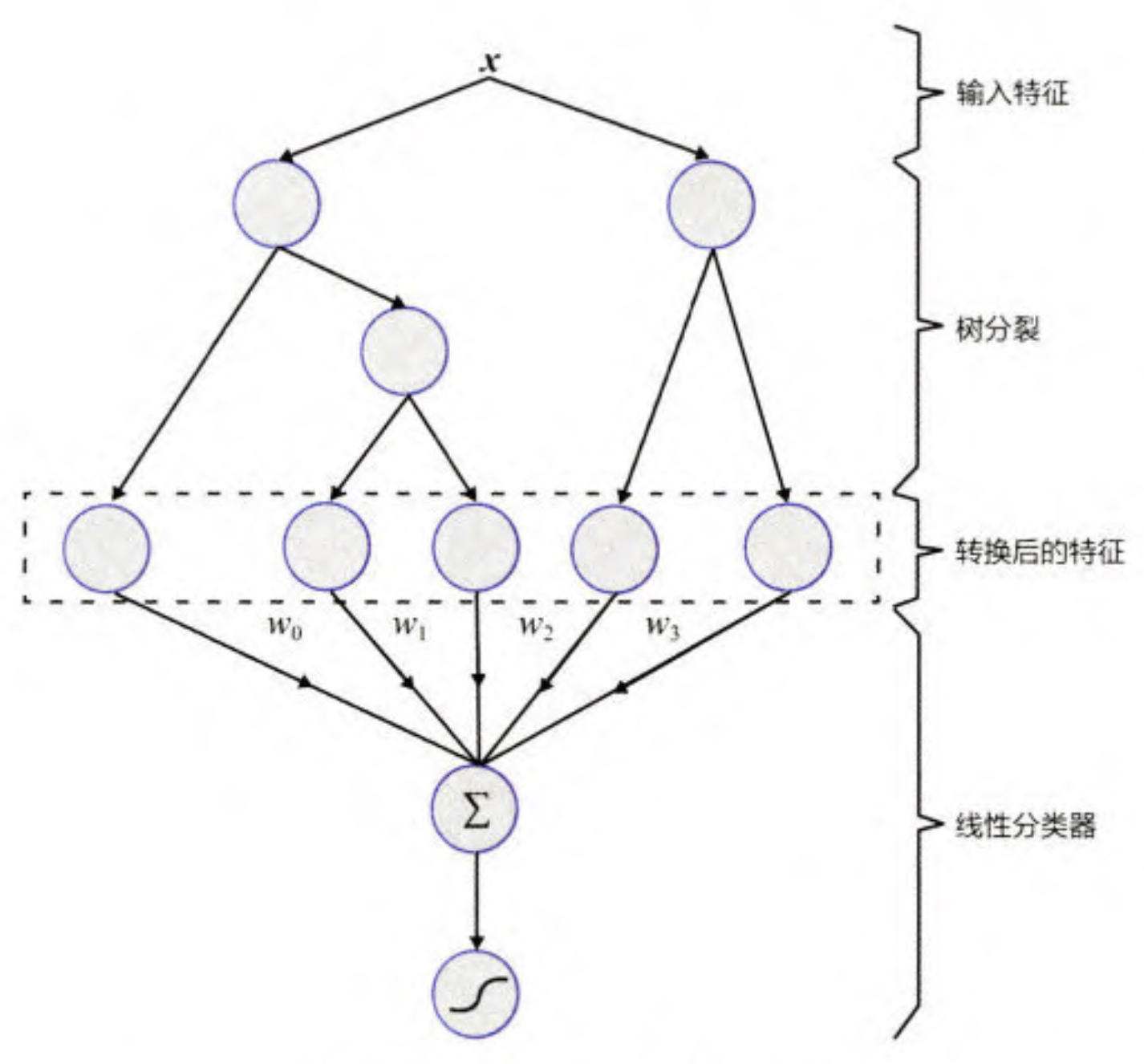
用 GBDT 构建特征工程,利用 LR 预估 CTR 这两步是独立 训练的,所以不存在如何将 LR 的梯度回传到 GBDT 这类复杂的问题。
GBDT
这里简单的介绍一下 GBDT的结构,如图2所示
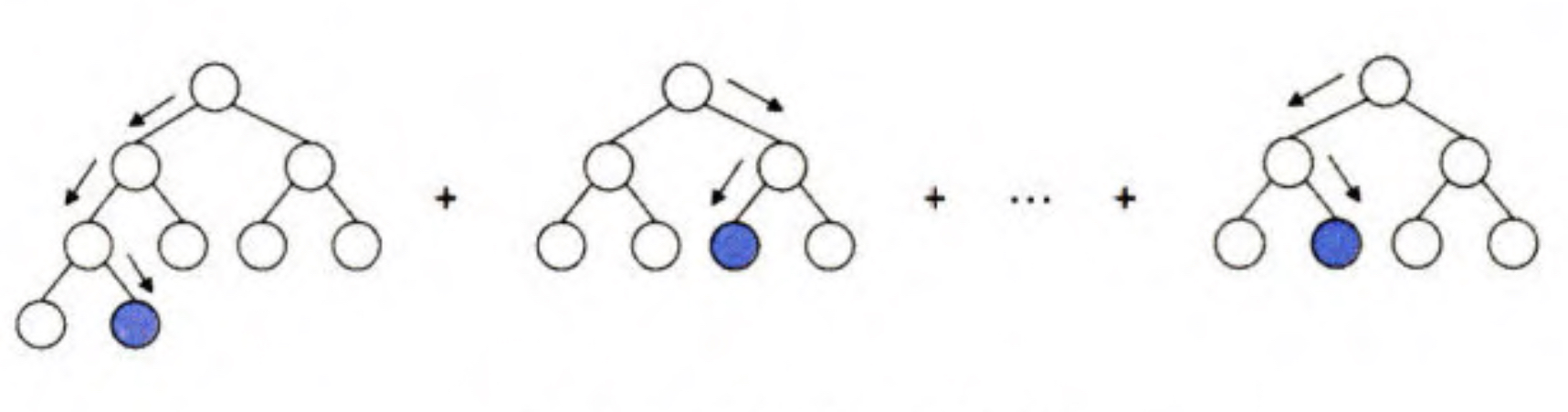
GBDT 通过逐一生成决策子树的方式生成整个树林,生成新子树的过程是 利用样本标签值与当前树林预测值之间的残差,构建新的子树。
形式化的表达就是
D(x)=tree1(x)+...,treen(x)(1.1)
D(x)就表示最终的得分。
理论上,如果可以无限生成决策树,那么 GBDT 可以无限逼近由所有训练集样本组成的目标拟合函数,从而达到减小预测误差的目的。
GBDT是由多棵回归树组成的树林,后一棵树以前面树林的结果与真实结果 的残差为拟合目标。每棵树生成的过程是一棵标准的回归树生成过程,因此回归树中每个节点的分裂是一个自然的特征选择的过程,而多层节点的结构则对特征进行了有效的自动组合,也就非常高效地解决了过去棘手的特征选择和特征组合 的问题。
GBDT做特征转化
GBDT训练好以后,就可以利用该模型完成从原始特征向量到新的离散型特征向量的转化。
一个训练样本在输人 GBDT 的某一子树后,会根据每个节点的规则最终落入某一叶子节点,把该叶子节点置为 1,其他叶子节点置为 0, 所有叶子节点组成的向量即形成了该棵树的特征向量,把 GBDT 所有子树的特征向量连接起来,即 形成了后续 LR 模型输人的离散型特征向量。
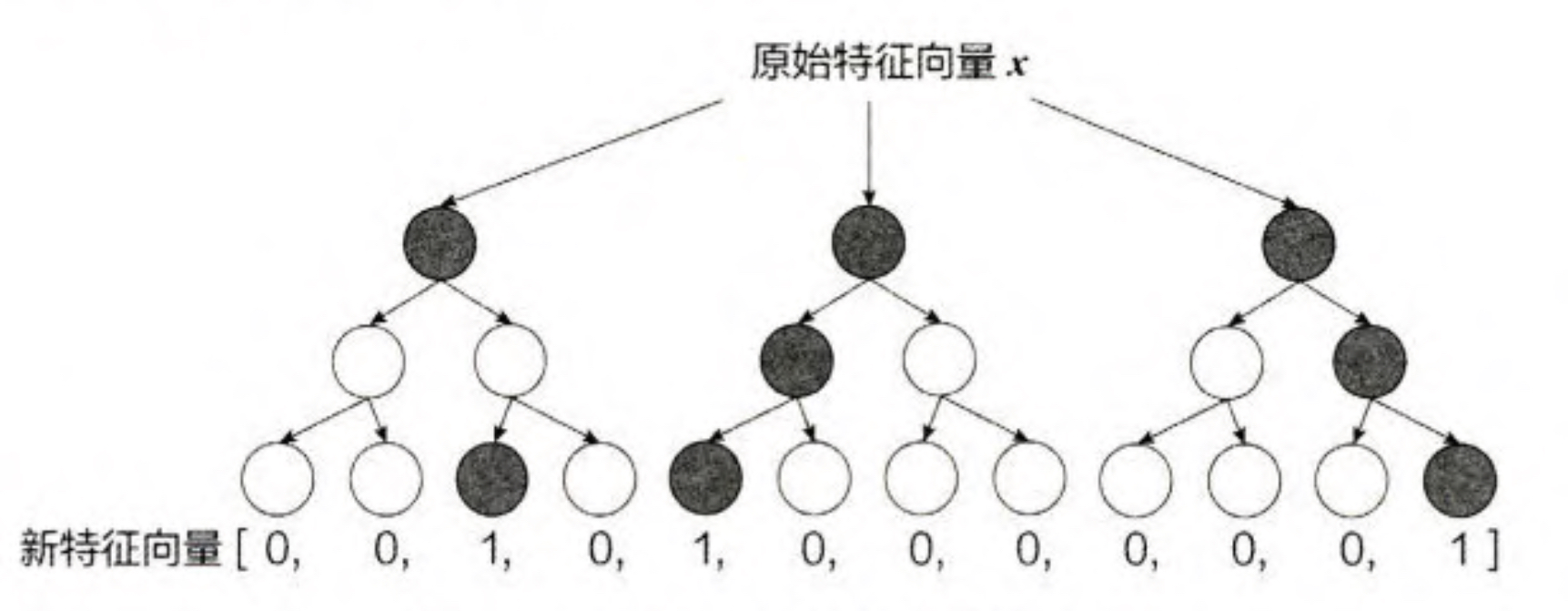
对于图3来讲,将原始的特征向量灌入到森林中,如果大部分节点落入了第一颗树的的第三个节点中,那么会形成[0,0,1,0]的子向量,决策树的深度决定了特征交叉的阶数。这样就得到了交叉以后的特征, 如果决策树的深度为 4, 则 通过 3 次节点分裂,最终的叶节点实际上是进行三阶特征组合后的结果,如此强的特征组合能力显然是FM系的模型不具备的。但GBDT容易产生过拟合,以及 GBDT 的特征转换方式实际上丢失了大量特征的数值信息,因此不能简单地说 GBDT 的特征交叉能力强,效果就比 FFM 好,在模型的选择和调试上,永远都是多种因素综合作用的结果。
重要意义
GBDT+LR 组合模型对于推荐系统领域的重要性在于,它大大推进了特征工 程模型化这一重要趋势。在 GBDT+LR 组合模型出现之前,特征工程的主要解决 方法有两个:一是进行人工的或半人工的特征组合和特征筛选;二是通过改造目 标函数 ,改进模型结构 ,增加特征交叉项的方式增强特征组合能力。但这两种方 法都有弊端,第一种方法对算法工程师的经验和精力投人要求较高;第二种方法 则要求从根本上改变模型结构,对模型设计能力的要求较高。