#凸优化
其实在我看来,大部分算法解决的问题其实就是一个又一个的优化问题,不管使用梯度下降或是其他的策略都是渴望能从解集中获取一个最优解,那么我们就来讲讲凸优化的相关理论,可能很枯燥,还是希望读者能够一起学习起来。
面对一个问题之前,我们要进行一层数学抽象,下面我们就给出我们是要解决一个怎样的问题。
$$minimize\ f(x)$$
$$sbj.\ x\in \Omega$$
在定义域x全集中,我们怎么选择怎样的x,让f(x)最小。
对于一个n维空间的函数,它的梯度正好是函数的一阶导数,这句抽象,直接举例。
对于 $f=5x_1+8x_2+x_1x_2$,它的一阶导数是
$$Df(x)=[5+x_2, 8+x_1]$$
这个实际就是一个多元函数的一阶导数,其实也就是它的梯度的转置。
这时候你是不是有另一个疑问,那二阶导数怎么表述呢?
二阶导数实际就是这个函数的黑塞矩阵。
推论:如果多元实值函数f在约束集合内一阶连续可微,那f的局部最小点满足
$$f(x)'=0$$
一阶导数是自变量的变化率,二阶导数就是一阶导数的变化率,也就是一阶导数变化率的变化率。
连续函数的一阶导数就是相应的切线斜率。一阶导数大于0,则递增;一阶倒数小于0,则递减;一阶导数等于0,则不增不减。
而二阶导数可以反映图象的凹凸。二阶导数大于0,图象为凹;二阶导数小于0,图象为凸;二阶导数等于0,不凹不凸。
结合一阶、二阶导数可以求函数的极值。当一阶导数等于零,而二阶导数大于零时,为极小值点;当一阶导数等于零,而二阶导数小于零时,为极大值点;当一阶导数、二阶导数都等于零时,为驻点。
黑塞矩阵
黑塞矩阵(Hessian Matrix),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出,并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。
加入有有函数如下:
$$f(x_0,x_1,...,x_n)$$
如果f的所有二阶导数都存在, 那么f的海森矩阵即
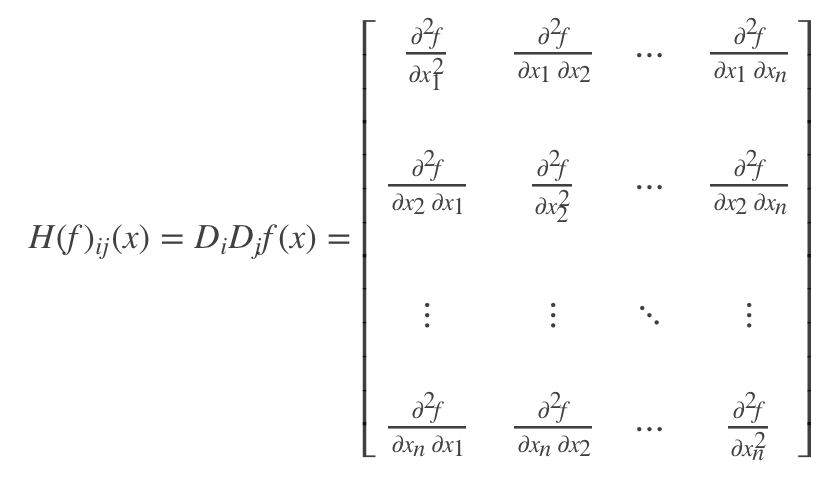
Hessian矩阵判断
(1)如果是正定矩阵,则临界点处是一个局部极小值
(2)如果是负定矩阵,则临界点处是一个局部极大值
(3)如果是不定矩阵,则临界点处不是极值
特征值:矩阵的特征值全大于零,矩阵为正定。矩阵的特征值全小于零,矩阵为负定。否则是不定的。